資料結構基礎之圖(下):最短路徑
轉自:http://www.cnblogs.com/edisonchou/p/4691020.html
圖(下):最短路徑
圖的最重要的應用之一就是在交通運輸和通訊網路中尋找最短路徑。例如在交通網路中經常會遇到這樣的問題:兩地之間是否有公路可通;在有多條公路可通的情況下,哪一條路徑是最短的等等。這就是帶權圖中求最短路徑的問題,此時路徑的長度不再是路徑上邊的數目總和,而是路徑上的邊所帶權值的和。帶權圖分為無向帶權圖和有向帶權圖,但如果從A地到B地有一條公路,A地和B地的海拔高度不同,由於上坡和下坡的車速不同,那麼邊<A,B>和邊<B,A>上表示行駛時間的權值也不同。考慮到交通網路中的這種有向性,本篇也只討論有向帶權圖的最短路徑。一般習慣將路徑的開始頂點成為源點,路徑的最後一個頂點成為終點。
一、單源點最短路徑
單源點最短路徑是指給定一個出發點(源點)和一個有向圖,求出源點到其他各頂點之間的最短路徑。對於下圖左邊所示的有向圖G,設頂點0為源點,則其到其他各頂點的最短路徑如下圖右邊所示。
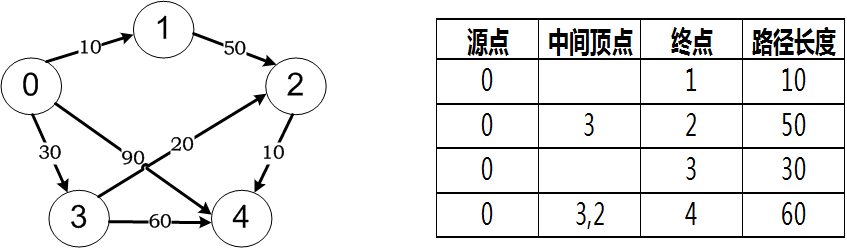
從上圖中可以看出,從源點0到終點4一共有4條路徑:
(1)0→4 路徑長度:90
(2)0→3→4 路徑長度:90
(3)0→1→2→4 路徑長度:70
(4)0→3→2→4 路徑長度:60
可以看出,源點0到終點4的最短路徑為第(4)條路徑。為了求出最短路徑,前人們已經做很多工作,為我們奉獻了兩個重要的演算法:Dijkstra(迪傑斯特拉)和Floyd(弗洛伊德)演算法,下面我們就來看看這兩個演算法。
二、Dijkstra演算法
2.1 演算法思想

Dijkstra在對最短路徑的求解方式做了大量的觀察之後,首先提出了按路徑長度遞增產生與頂點之間的路徑最短的演算法,以他的名字稱之為Dijkstra演算法。
Dijkstra演算法的基本思想是:將圖中頂點的集合分為兩組S和U,並按最短路徑長度的遞增次序依次將集合U中的頂點加入到S中,在加入的過程中,總保持從原點v到S中各頂點的最短路徑長度不大於從原點v到U中任何頂點的最短路徑長度。
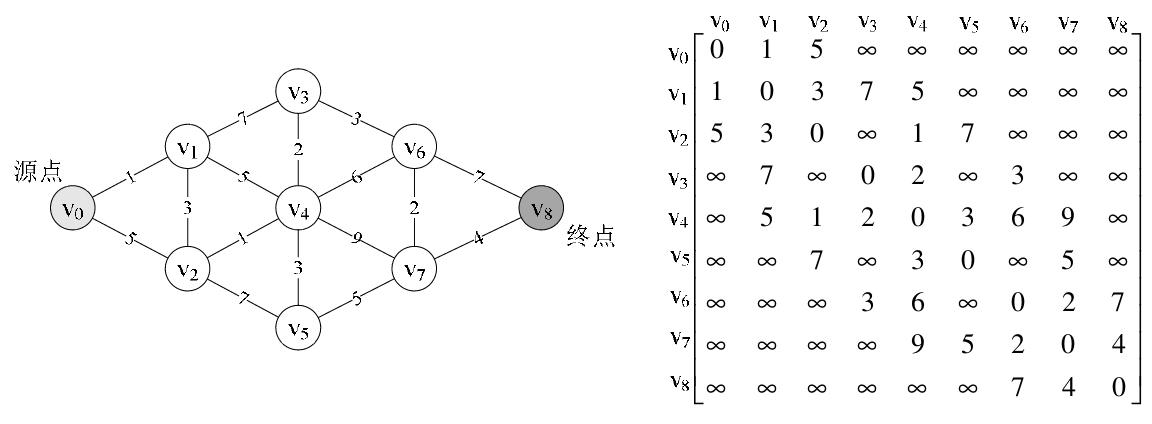
Dijkstra演算法採用鄰接矩陣儲存圖的資訊並計算源點到圖中其餘頂點的最短路徑,如下圖所示。
2.2 演算法實現
(1)程式碼實現
static void Dijkstra(int[,] cost, int v)
{
int n = cost.GetLength(1); // 計算頂點個數
int[] s = new int[n]; // 集合S
int[] dist = new int[n]; // 結果集
int[] path = new int[n]; // 路徑集
for (int i = 0; i < n; i++)
{
// 初始化結果集
dist[i] = cost[v, i];
// 初始化路徑集
if (cost[v, i] > 0)
{
// 如果源點與頂點存在邊
path[i] = v;
}
else
{
// 如果源點與頂點不存在邊
path[i] = -1;
}
}
s[v] = 1; // 將源點加入集合S
path[v] = 0;
for (int i = 0; i < n; i++)
{
int u = 0; // 指示剩餘頂點在dist集合中的最小值的索引號
int minDis = int.MaxValue; // 指示剩餘頂點在dist集合中的最小值大小
// 01.計算dist集合中的最小值
for (int j = 0; j < n; j++)
{
if (s[j] == 0 && dist[j] > 0 && dist[j] < minDis)
{
u = j;
minDis = dist[j];
}
}
s[u] = 1; // 將抽出的頂點放入集合S中
// 02.計算源點經過頂點u到其餘頂點的距離
for (int j = 0; j < n; j++)
{
// 如果頂點不在集合S中
if (s[j] == 0)
{
// 加入的頂點如與其餘頂點存在邊,並且重新計算的值小於原值
if (cost[u, j] > 0 && (dist[j] == 0 || dist[u] + cost[u, j] < dist[j]))
{
// 計算更小的值代替原值
dist[j] = dist[u] + cost[u, j];
path[j] = u;
}
}
}
}
// 列印源點到各頂點的路徑及距離
for (int i = 0; i < n; i++)
{
if (s[i] == 1)
{
Console.Write("從{0}到{1}的最短路徑為:", v, i);
Console.Write(v + "→");
// 使用遞迴獲取指定頂點在路徑上的前一頂點
GetPath(path, i, v);
Console.Write(i + Environment.NewLine + "SUM:");
Console.WriteLine("路徑長度為:{0}", dist[i]);
}
}
}
static void GetPath(int[] path, int i, int v)
{
int k = path[i];
if (k == v)
{
return;
}
GetPath(path, k, v);
Console.Write(k + "→");
}
這裡經歷了三個步驟,第一步是構造集合U,第二步是尋找最短路徑,第三步是重新計算替換原有路徑。
(2)基本測試
這裡要構造的有向帶權圖如下圖所示:
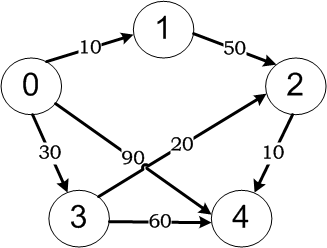

static void DijkstraTest()
{
int[,] cost = new int[5, 5];
// 初始化鄰接矩陣
cost[0, 1] = 10;
cost[0, 3] = 30;
cost[0, 4] = 90;
cost[1, 2] = 50;
cost[2, 4] = 10;
cost[3, 2] = 20;
cost[3, 4] = 60;
// 使用Dijkstra演算法計算最短路徑
Dijkstra(cost, 0);
}
執行結果如下圖所示:

從圖中可以看出,從源點0到終點4的最短路徑為:0→3→2→4,該路徑長度為60。
三、Floyd演算法
3.1 演算法思想

Floyd(弗洛伊德)演算法提出了另外一種用於計算有向圖中所有頂點間的最短路徑,這種演算法成為Floyd演算法,它的形式較Dijkstra演算法更為簡單。
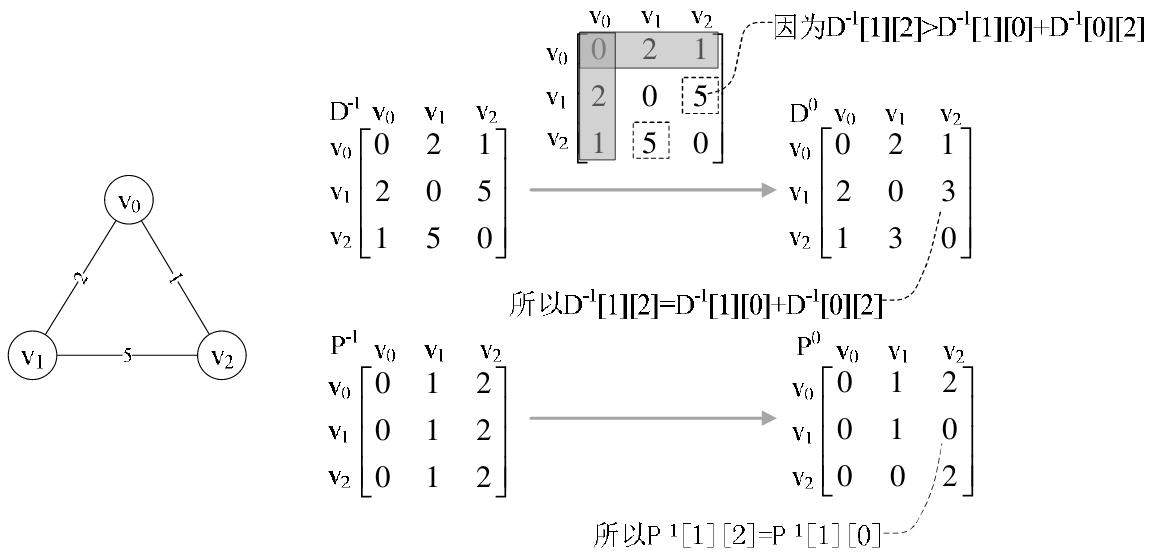
Floyd演算法仍然使用鄰接矩陣儲存的圖,同時定義了一個二維陣列A,其中每一個分量A[i,j]是頂點i到頂點j的最短路徑長度。另外還使用了另一個二維陣列path來儲存最短路徑資訊。Floyd演算法的基本思想如下:
(1)初始時,對圖中任意兩個頂點Vi和Vj,如果從Vi到Vj存在邊,則從Vi到Vj存在一條長度為cost[i,j]的路徑,但該路徑不一定是最短路徑。初始化時,A[i,j]=cost[i,j]。
(2)在圖中任意兩個頂點Vi和Vj之間加入頂點Vk,如果Vi經Vk到達Vj的路徑存在並更短,則用A[i,k]+A[k,j]的值代替原來的A[i,j]值。
(3)重複步驟(2),直到將所有頂點作為中間點依次加入集合中,並通過迭代公式不斷修正A[i,j]的值,最終獲得任意頂點的最短路徑長度。
3.2 演算法實現
(1)程式碼實現
static void Floyd(int[,] cost, int v)
{
int n = cost.GetLength(1); // 獲取頂點個數
int[,] A = new int[n, n]; // 存放最短路徑長度
int[,] path = new int[n, n];// 存放最短路徑資訊
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
// 輔助陣列A和path的初始化
A[i, j] = cost[i, j];
path[i, j] = -1;
}
}
// Flyod演算法核心程式碼部分
for (int k = 0; k < n; k++)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
// 如果存在中間頂點K的路徑
if (i != j && A[i, k] != 0 && A[k, j] != 0)
{
// 如果加入中間頂點k後的路徑更短
if (A[i, j] == 0 || A[i, j] > A[i, k] + A[k, j])
{
// 使用新路徑代替原路徑
A[i, j] = A[i, k] + A[k, j];
path[i, j] = k;
}
}
}
}
}
// 列印最短路徑及路徑長度
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (A[i, j] == 0)
{
if (i != j)
{
Console.WriteLine("從{0}到{1}沒有路徑!", i, j);
}
}
else
{
Console.Write("從{0}到{1}的路徑為:", i, j);
Console.Write(i + "→");
// 使用遞迴獲取指定頂點的路徑
GetPath(path, i, j);
Console.Write(j + " ");
Console.WriteLine("路徑長度為:{0}", A[i, j]);
}
}
Console.WriteLine();
}
}
static void GetPath(int[,] path, int i, int j)
{
int k = path[i, j];
if (k == -1)
{
return;
}
GetPath(path, i, k);
Console.Write(k + "→");
GetPath(path, k, j);
}
(2)基本測試

static void FloydTest()
{
int[,] cost = new int[5, 5];
// 初始化鄰接矩陣
cost[0, 1] = 10;
cost[0, 3] = 30;
cost[0, 4] = 90;
cost[1, 2] = 50;
cost[2, 4] = 10;
cost[3, 2] = 20;
cost[3, 4] = 60;
// 使用Flyod演算法計算最短路徑
Floyd(cost, 0);
}
執行結果如下圖所示:
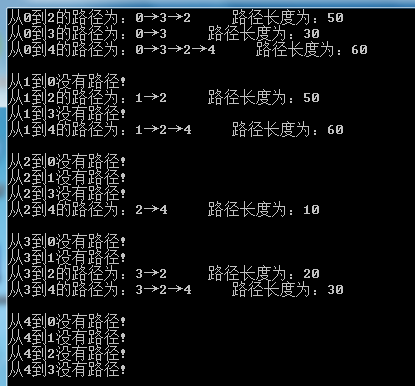
參考資料
(1)程傑,《大話資料結構》
(2)陳廣,《資料結構(C#語言描述)》
(3)段恩澤,《資料結構(C#語言版)》
作者:周旭龍
出處:http://edisonchou.cnblogs.com
本文版權歸作者和部落格園共有,歡迎轉載,但未經作者同意必須保留此段宣告,且在文章頁面明顯位置給出原文連結。