資料結構基礎之圖(中):圖的遍歷演算法
轉自:http://www.cnblogs.com/edisonchou/p/4676876.html
圖(中):圖的遍歷演算法
上一篇我們瞭解了圖的基本概念、術語以及儲存結構,還對鄰接表結構進行了模擬實現。本篇我們來了解一下圖的遍歷,和樹的遍歷類似,從圖的某一頂點出發訪問圖中其餘頂點,並且使每一個頂點僅被訪問一次,這一過程就叫做圖的遍歷(Traversing Graph)。如果只訪問圖的頂點而不關注邊的資訊,那麼圖的遍歷十分簡單,使用一個foreach語句遍歷存放頂點資訊的陣列即可。但是,如果為了實現特定演算法,就必須要根據邊的資訊按照一定的順序進行遍歷。圖的遍歷演算法是求解圖的連通性問題、拓撲排序和求解關鍵路徑等演算法的基礎。
一、圖的遍歷
圖的遍歷要比樹的遍歷複雜得多,由於圖的任一頂點都可能和其餘頂點相鄰接,所以在訪問了某頂點之後,可能順著某條邊又訪問到了已訪問過的頂點。因此,在圖的遍歷過程中,必須記下每個訪問過的頂點,以免同一個頂點被訪問多次。為此,給頂點附加一個訪問標誌isVisited,其初值為false,一旦某個頂點被訪問,則將其isVisited標誌設為true。
protected class Vertex<TValue>
{
public TValue data; // 資料
public Node firstEdge; // 鄰接點連結串列頭指標
public bool isVisited; // 訪問標誌:遍歷時使用
public Vertex()
{
this.data = default(TValue);
}
public Vertex(TValue value)
{
this.data = value;
}
}在上面的頂點類的定義中,增加了一個bool型別的成員isVisited,用於在遍歷時判斷是否已經訪問過了該頂點。一般在進行遍歷操作時,會首先將所有頂點的isVisited屬性置為false,於是可以寫一個輔助方法InitVisited(),如下所示:
/// <summary>
/// 輔助方法:初始化頂點的visited標誌為false
/// </summary>
private void InitVisited()
{
foreach (Vertex<T> v in items)
{
v.isVisited = false;
}
}圖的遍歷方法主要有兩種:一種是深度優先搜尋遍歷(Depth-First Search,DFS),另一種是廣度優先搜尋遍歷(Breadth-First Search,BFS)。下面,我們就來仔細看看這兩種圖的遍歷演算法。
二、深度優先搜尋遍歷
2.1 深度優先遍歷原理
圖的深度優先遍歷類似於二叉樹的深度優先遍歷,其基本思想是:從圖中某個頂點v出發,訪問此頂點,然後從v的未被訪問的鄰接點出發深度優先遍歷圖,直至圖中所有和v有路徑相通的頂點都被訪問到。顯然,這是一個遞迴的搜尋過程。
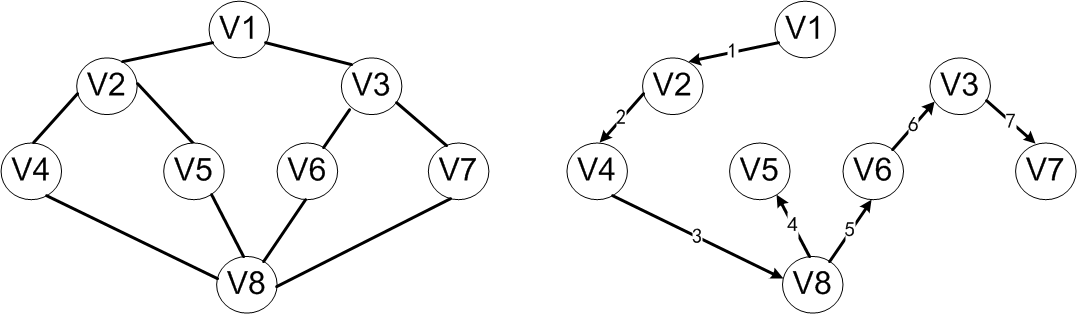
以上圖為例,假定V1是出發點,首先訪問V1。這時兩個鄰接點V2、V3均未被訪問,可以選擇V2作為新的出發點,訪問V2之後,再找到V2的未訪問過的鄰接點。同V2鄰接的有V1、V4和V5,其中V1已經訪問過了,可以選擇V4作為新的出發點。重複上述搜尋過程,繼續依次訪問V8、V5。訪問V5之後,由於與V5相鄰的頂點均已被訪問過,搜尋退回到V8,訪問V8的另一個鄰接點V6.接下來依次訪問V3和V7,最後得到的訪問序列為V1→V2→V4→V8→V5→V6→V3→V7。
2.2 深度優先遍歷實現
(1)實現程式碼
/// <summary>
/// 深度優先遍歷介面For連通圖
/// </summary>
public void DFSTraverse()
{
InitVisited(); // 首先初始化visited標誌
DFS(items[0]); // 從第一個頂點開始遍歷
}
/// <summary>
/// 深度優先遍歷演算法
/// </summary>
/// <param name="v">頂點</param>
private void DFS(Vertex<T> v)
{
v.isVisited = true; // 首先將訪問標誌設為true標識為已訪問
Console.Write(v.data.ToString() + " "); // 進行訪問操作:這裡是輸出頂點data
Node node = v.firstEdge;
while (node != null)
{
if (node.adjvex.isVisited == false) // 如果鄰接頂點未被訪問
{
DFS(node.adjvex); // 遞迴訪問node的鄰接頂點
}
node = node.next; // 訪問下一個鄰接點
}
}
深度優先遍歷是一個典型的遞迴過程,這裡也使用了遞迴的方式。
(2)遍歷測試
這裡的測試程式碼構造的圖如下所示:

測試程式碼如下所示:

static void MyAdjacencyListDFSTraverseTest()
{
Console.Write("深度優先遍歷:");
MyAdjacencyList<string> adjList = new MyAdjacencyList<string>();
// 新增頂點
adjList.AddVertex("V1");
adjList.AddVertex("V2");
adjList.AddVertex("V3");
adjList.AddVertex("V4");
adjList.AddVertex("V5");
adjList.AddVertex("V6");
adjList.AddVertex("V7");
adjList.AddVertex("V8");
// 新增邊
adjList.AddEdge("V1", "V2");
adjList.AddEdge("V1", "V3");
adjList.AddEdge("V2", "V4");
adjList.AddEdge("V2", "V5");
adjList.AddEdge("V3", "V6");
adjList.AddEdge("V3", "V7");
adjList.AddEdge("V4", "V8");
adjList.AddEdge("V5", "V8");
adjList.AddEdge("V6", "V8");
adjList.AddEdge("V7", "V8");
// DFS遍歷
adjList.DFSTraverse();
Console.WriteLine();
}
執行結果如下圖所示:

三、廣度優先搜尋遍歷
3.1 廣度優先遍歷原理
圖的廣度優先遍歷演算法是一個分層遍歷的過程,和二叉樹的廣度優先遍歷類似,其基本思想在於:從圖中的某一個頂點Vi觸發,訪問此頂點後,依次訪問Vi的各個為層訪問過的鄰接點,然後分別從這些鄰接點出發,直至圖中所有頂點都被訪問到。
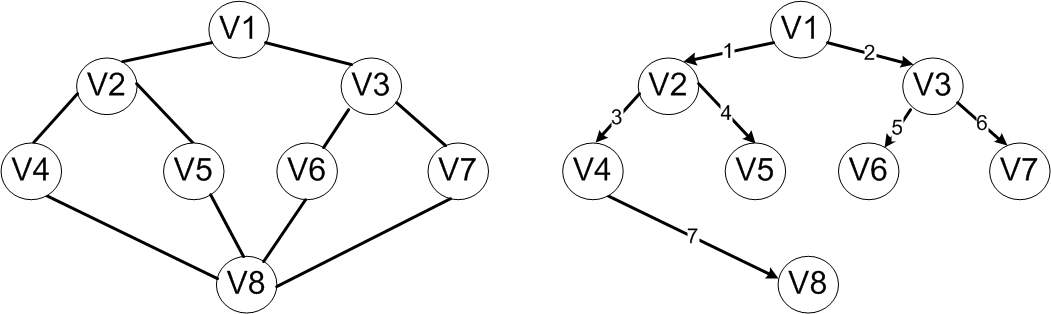
對於上圖所示的無向連通圖,若從頂點V1開始,則廣度優先遍歷的頂點訪問順序是V1→V2→V3→V4→V5→V6→V7→V8。
3.2 廣度優先遍歷實現
(1)實現程式碼
/// <summary>
/// 寬度優先遍歷介面For連通圖
/// </summary>
public void BFSTraverse()
{
InitVisited(); // 首先初始化visited標誌
BFS(items[0]); // 從第一個頂點開始遍歷
}
/// <summary>
/// 寬度優先遍歷演算法
/// </summary>
/// <param name="v">頂點</param>
private void BFS(Vertex<T> v)
{
v.isVisited = true; // 首先將訪問標誌設為true標識為已訪問
Console.Write(v.data.ToString() + " "); // 進行訪問操作:這裡是輸出頂點data
Queue<Vertex<T>> verQueue = new Queue<Vertex<T>>(); // 使用佇列儲存
verQueue.Enqueue(v);
while (verQueue.Count > 0)
{
Vertex<T> w = verQueue.Dequeue();
Node node = w.firstEdge;
// 訪問此頂點的所有鄰接節點
while (node != null)
{
// 如果鄰接節點沒有被訪問過則訪問它的邊
if (node.adjvex.isVisited == false)
{
node.adjvex.isVisited = true; // 設定為已訪問
Console.Write(node.adjvex.data + " "); // 訪問
verQueue.Enqueue(node.adjvex); // 入隊
}
node = node.next; // 訪問下一個鄰接點
}
}
}
和樹的層次遍歷類似,藉助了佇列這一資料結構進行輔助,記錄頂點的鄰接點。
(2)遍歷測試
這裡構造的圖如下所示,跟上面原理中的圖一致:

測試程式碼如下所示:

static void MyAdjacencyListTraverseTest()
{
MyAdjacencyList<string> adjList = new MyAdjacencyList<string>();
// 新增頂點
adjList.AddVertex("V1");
adjList.AddVertex("V2");
adjList.AddVertex("V3");
adjList.AddVertex("V4");
adjList.AddVertex("V5");
adjList.AddVertex("V6");
adjList.AddVertex("V7");
adjList.AddVertex("V8");
// 新增邊
adjList.AddEdge("V1", "V2");
adjList.AddEdge("V1", "V3");
adjList.AddEdge("V2", "V4");
adjList.AddEdge("V2", "V5");
adjList.AddEdge("V3", "V6");
adjList.AddEdge("V3", "V7");
adjList.AddEdge("V4", "V8");
adjList.AddEdge("V5", "V8");
adjList.AddEdge("V6", "V8");
adjList.AddEdge("V7", "V8");
Console.Write("廣度優先遍歷:");
// BFS遍歷
adjList.BFSTraverse();
Console.WriteLine();
}
執行結果如下圖所示:

四、非連通圖的遍歷
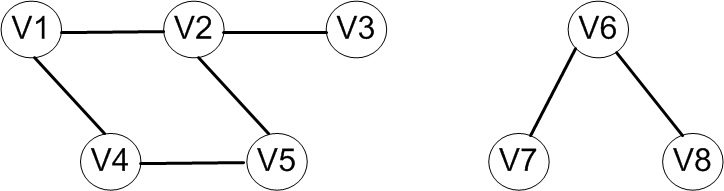
以上討論的圖的兩種遍歷方法都是針對無向連通圖的,它們都是從一個頂點觸發就能訪問到圖中的所有頂點。若無方向圖是非連通圖,則只能訪問到初始點所在連通分量中的所有頂點,其他分量中的頂點是無法訪問到的。如下圖所示,V6、V7以及V8三個頂點均訪問不到。為此,需要從其他每個連通分量中選擇初始點,分別進行遍歷,才能夠訪問到圖中的所有頂點。
4.1 非連通圖的深度優先遍歷實現
/// <summary>
/// 深度優先遍歷介面For非聯通圖
/// </summary>
public void DFSTraverse4NUG()
{
InitVisited();
foreach (var v in items)
{
if (v.isVisited == false)
{
DFS(v);
}
}
}
這裡DFS方法跟上面無向連通圖的保持一致。
4.2 非連通圖的廣度優先遍歷實現
/// <summary>
/// 廣度優先遍歷介面For非聯通圖
/// </summary>
public void BFSTraverse4NUG()
{
InitVisited();
foreach (var v in items)
{
if (v.isVisited == false)
{
BFS(v);
}
}
}
這裡BFS方法跟上面無向連通圖的保持一致。
4.3 非連通圖的遍歷測試
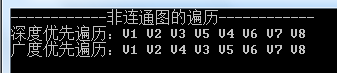
構造的圖如上圖所示,測試程式碼如下:

static void MyAdjacencyListTraverseTest()
{
Console.WriteLine("------------非連通圖的遍歷------------");
MyAdjacencyList<string> numAdjList = new MyAdjacencyList<string>();
// 新增頂點
numAdjList.AddVertex("V1");
numAdjList.AddVertex("V2");
numAdjList.AddVertex("V3");
numAdjList.AddVertex("V4");
numAdjList.AddVertex("V5");
numAdjList.AddVertex("V6");
numAdjList.AddVertex("V7");
numAdjList.AddVertex("V8");
// 新增邊
numAdjList.AddEdge("V1", "V2");
numAdjList.AddEdge("V1", "V4");
numAdjList.AddEdge("V2", "V3");
numAdjList.AddEdge("V2", "V5");
numAdjList.AddEdge("V4", "V5");
numAdjList.AddEdge("V6", "V7");
numAdjList.AddEdge("V6", "V8");
Console.Write("深度優先遍歷:");
// DFS遍歷
numAdjList.DFSTraverse4NUG();
Console.WriteLine();
Console.Write("廣度優先遍歷:");
// BFS遍歷
numAdjList.BFSTraverse4NUG();
}
執行結果如下圖所示:
附件下載
本篇實現的圖的遍歷演算法:code.datastructure.graph
參考資料
(1)程傑,《大話資料結構》
(2)陳廣,《資料結構(C#語言描述)》
(3)段恩澤,《資料結構(C#語言版)》
作者:周旭龍
出處:http://edisonchou.cnblogs.com
本文版權歸作者和部落格園共有,歡迎轉載,但未經作者同意必須保留此段宣告,且在文章頁面明顯位置給出原文連結。


