20172309_《程式設計與資料結構（下）》_課堂測試修改報告。
阿新 • • 發佈：2018-11-08
20172309_《程式設計與資料結構（下）》_課堂測試修改報告。
課程：《程式設計與資料結構》
班級：1723
姓名： 王志偉
學號：20172309
實驗教師：王志強老師
實驗日期：2018年6月13日
必修/選修： 必修
實驗內容：
- 查詢演算法綜合示例：
實驗過程及結果
- 畫出順序查詢的查詢順序表及成功查詢平均長度
- 順序表：
| 序列 | 11 | 78 | 10 | 1 | 3 | 2 | 4 | 21 |
|---|---|---|---|---|---|---|---|---|
| 查詢次數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
- 平均查詢長度：
ASL=(1+2+3+4+5+6+7+8)/8=4.5- 畫出折半查詢的判定樹並計算出平均查詢長度：
- 首先注意：進行二分查詢的必須是有序結構。 所以先排序： 1 2 3 4 10 11 21 78。
- 其次注意取中間值時:mid = (star+end)/2 取值定義為不超過mid的最大整數。
- 判定樹：
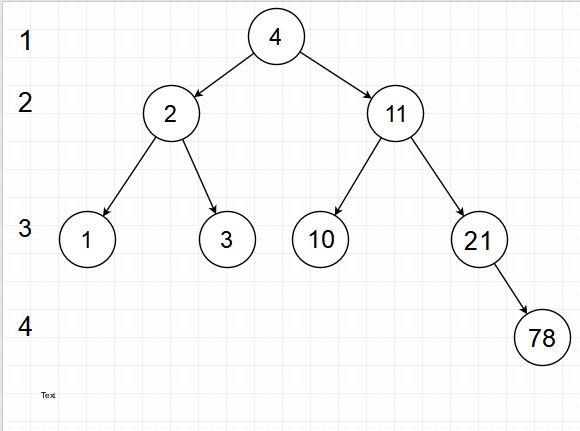(注：第一行說明在第一次就查詢到了。第二行說明在第二次找到了。以此類推···) - 平均查詢長度：
ASL=(1*1+2*2+3*4+4*1)/8=2.625 - 畫出雜湊查詢（線性探查法）的散列表和成功平均查詢長度
- 首先求出散列表的大小m：m一般取要排序數字的個數n的1.1~1.7倍，即1.1n<=m<=1.7n
- 然後對每個元素分別求模：
| 元素 | 11 | 78 | 10 | 1 | 3 | 2 | 4 | 21 |
|---|---|---|---|---|---|---|---|---|
| H(key)=key%m | 0 | 1 | 10 | 1 | 3 | 2 | 4 | 10 |
- 然後根據求得的mod,把元素插進去：
| 序列 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 查詢次數 | 11 | 78 | 1 | 3 | 2 | 4 | 21 | 10 |
- 這裡需要注意的是：
- 當插入元素1時，求得的模等於1.但是所在的位置已經有元素了，所以我們運用的方法是：H(key)=(key+1)%m,然後判斷此處所求的模的位置否有元素，如果有，則重複此操作；如果沒有，元素將被放在這。
- 當被插入的位置是最後一個但此處位置已經有元素時（比如插入元素21時），此時10的位置後面沒有位置！因此我們將元素從頭開始放，直至有位置。我的理解是將這個散列表看成一個環形陣列，然後後面沒位置時，從頭開始。
- 平均查詢長度：
ASL=(1+1+1+2+1+3+2+8)/8=19/8=2.375（注：括號中的次數分別對應著原列表中元素的順序。）
- 用雜湊連結串列法儲存元素：
這個平均查詢長度：
ASL=（6*1 + 2*2)/8=5/4=1.25
實驗過程中出現的問題：
- 問題一：第一種方案中，當在散列表中插入元素時，滿了怎麼辦？
解決方案：
當時想到這個問題感覺是這種儲存方式是錯的，現在想起來是自己太傻太天真了。然後下課後吃飯的時候，想了想，散列表m取1.1n~1.7n,也就是說m永遠比元素個數n大，怎麼會裝不下呢？
問題二：我當時是這麼做的
也就是說，我當時把散列表大小建立成12個，這為什麼錯了呢？因為當我們把散列表大小建立成12時，相當於我們求的模為13了（從零開始數的）。