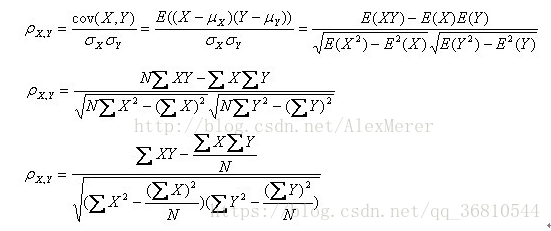N個向量間的兩兩皮爾遜係數的矩陣計算方法

目的：有N個行向量 $[\begin{matrix} e_{1}, \\ e_{2}, \\ . . . . \\ e_{n} \end{matrix}]$

e 2 , . . .

. e n ] $\begin{bmatrix} e_{1}, \\e_{2} ,\\....\\e_{n}\end{bmatrix}$ 需要計算兩兩之間的皮爾遜係數,最簡單的辦法就是兩個for迴圈，分別計算就搞定了。但是，如果n的值不大這樣還ok，一旦n的值很大一般在10W左右，再迴圈效率損失就不小了，在做科學計算的時候，能用矩陣運算的就儘量別用迴圈太耗時！
PS：程式碼裡連矩陣運算都沒有還怎麼愉快的裝X啊，哈哈
======================我是隻想安安靜靜寫程式碼的分割線===================
兩個向量的皮爾遜係數計算公式：
這裡寫圖片描述

有個更簡單的計算公式：

ρ_{x, y} = \frac{\sum_{i = 1}^{n} (x - \bar{x}) \cdot (y - \bar{y})}{\sqrt{\sum_{i = 1}^{n} (x - \bar{x})^{2} \cdot \sum_{i = 1}^{n} (y - \bar{y})^{2}}}

$\rho_{x,y}= \frac{\sum_{i=1}^{n}(x-\bar{x})\cdot (y-\bar{y})}{\sqrt{\sum_{i=1}^{n}(x-\bar{x})^{2}\cdot\sum_{i=1}^{n}(y-\bar{y})^{2}}}$
根據公式寫出對應的程式碼：

 # 計算兩序列的皮爾遜係數，數值越大相關性越大
 def get_distance(self, vector1, vector2):
     num1 = vector1 - np.average(vector1)
     num2 = vector2 - np.average(vector2)
     num = np.sum(num1 * num2)
     den = np.sqrt(np.sum(np.power(num1,2)) * np.sum(np.power(num2,2)))
     if den == 0:
         return 0.0
     return np.abs(num/den)

現在來利用矩陣重寫上述公式：
$e-\bar{e} = \tilde{e} = \begin{bmatrix}e_{1} - \bar{e_{1}}\\ e_{2} - \bar{e_{2}}\\ .....\\ e_{n} - \bar{e_{n}}\end{bmatrix}$

$\tilde{e}=\begin{bmatrix}\tilde{e_{1}}\\ \tilde{e_{2}}\\ ...\\ \tilde{e_{n}}\end{bmatrix}$
則有：
$\tilde{e} \cdot {\tilde{e}}^{'} = [\begin{matrix} {\tilde{e_{1}}}^{2}, \tilde{e_{1}} \cdot \tilde{e_{2}}, . ., \tilde{e_{1}} \cdot \tilde{e_{n}} \\ \tilde{e_{2}} \cdot \tilde{e_{1}}, {\tilde{e_{2}}}^{2}, . . ., \tilde{e_{2}} \cdot \tilde{e_{n}} \\ . . . \\ \tilde{e_{n}} \cdot \tilde{e_{1}}, \tilde{e_{n}} \cdot \tilde{e_{2}}, . . ., {\tilde{e_{n}}}^{2} \end{matrix}]$

N個向量間的兩兩皮爾遜係數的矩陣計算方法

N個向量間的兩兩皮爾遜係數的矩陣計算方法

Scala實現Pearson皮爾遜相似度計算

推薦演算法之-皮爾遜相關係數計算兩個使用者喜好相似度

（轉載）求1到n這n個整數間的異或值（O(1)演算法）

CreateFileMapping在N個程序間共享一個HWND型別記憶體

皮爾遜相關系數

皮爾遜相關系數和余弦相似性的關系

皮爾遜相關系數理解

np.corrcoef()方法計算數據皮爾遜積矩相關系數（Pearson's r）

【Python學習筆記】使用Python計算皮爾遜相關系數

皮爾遜系數

Neo4j 做推薦（11）—— 協同過濾（皮爾遜相似性）

使用者推薦演算法 pearson（皮爾遜）相似度

Pearson(皮爾遜)相關係數

Python基於皮爾遜系數實現股票預測（多線程）

皮爾遜相關係數和餘弦相似度

【126】TensorFlow 使用皮爾遜相關係數找出和標籤相關性最大的特徵值

皮爾遜相關系數（Pearson Correlation Coefficient, Pearson's r）

集體智慧程式設計-皮爾遜相關係數程式碼理解

皮爾遜相關系數與余弦相似度（Pearson Correlation Coefficient & Cosine Similarity）

N個向量間的兩兩皮爾遜係數的矩陣計算方法

相關推薦