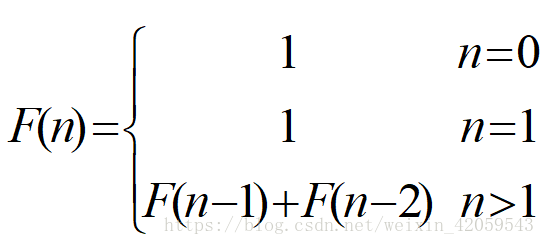無窮數列1，1，2，3，5，8，13，21，34，55，……，稱為Fibonacci數列。它可以遞迴地定義為：

第n個Fibonacci數可遞迴地計算如下：

int fibonacci(int n)

   {

       if (n <= 1) return 1;

       return fibonacci(n-1)+fibonacci(n-2);

   }

1) 編寫完整的主函式，分別記錄利用上述遞迴函式求第45,46,47,48個Fibonacci數所花費的時間。

2）將遞迴函式改為尾遞迴，或者是遞推函式，求第45,46,47,48個Fibonacci數所花費的時間，觀察效率是否得到提高。

1）

import java.util.Date;
public class S2_1 {

	public static void main(String[] args) {
		S2_1 sc=new S2_1();
		for(int i=45;i<=48;i++){
		long startTime = new Date().getTime();
		System.out.println("第"+i+"個結果為 "+sc.fibonacci(i));
		long endTime = new Date().getTime();
		System.out.println("本程式執行 " + (endTime - startTime)+ " 毫秒完成。" );
		}
	}
	int fibonacci(int n)
	{
	if (n == 1 || n==0) return 1;
	return fibonacci(n-1)+fibonacci(n-2);
	}
}
 

2）

import java.util.Date;
public class S2_2 {

	public static void main(String[] args) {
		S2_2 sc=new S2_2();
		for(int i=45;i<=48;i++){
		long startTime = new Date().getTime();
		System.out.println("第"+i+"個結果為 "+sc.fibonacci(i));
		long endTime = new Date().getTime();
		System.out.println("本程式執行 " + (endTime - startTime)+ " 毫秒完成。" );
		}
	}
	int fibonacci(int n)
	{
	    int f0 = 1;
	    int f1 = 1;
	    int fn=0;
	    if (n == 0 || n == 1)
	        return 1;

	    for (int i = 2;i <= n;i++)
	    {
	        fn = f0 + f1;
	        f0 = f1;
	        f1 = fn;
	    }
	    return fn;
	}
}
 

Fibonacci的奇偶性

Fibonacci數列定義如下： a[1]=1； a[2]=1； a[n]=a[n-1]+a[n-2]（n>2）。 對於給定N (1≤N≤10000)，請判別數列第N項的奇偶性。

給定整數N，如N=0則結束輸入（N=0不需要判斷）。

輸出第N項Fibonacci數列的奇偶性，如果為奇數則請輸出“ODD”，否則為“EVEN”。

import java.util.*;
public class S2_1091 {

	public static void main(String[] args) {
		int A[]=new int[1000];
		S2_1091 sc=new S2_1091();
		Scanner s=new Scanner(System.in);
		System.out.print("輸入N（1~10000）:");
		int n=s.nextInt();
		int i=0;
		while(n!=0) {
			A[i]=sc.fibonacci(n);
			i++;	
			n=s.nextInt();
		}
		for(int j=0;j<i;j++) {
		if(A[j]%2==1) {
			System.out.println("ODD");
		}else {
			System.out.println("EVEN");
		}
		}
	}
	int fibonacci(int n)
	{
	    int f1 = 1;
	    int f2 = 1;
	    int fn=0;
	    if (n == 1 || n == 2)
	        return 1;

	    for (int i = 3;i <= n;i++)
	    {
	        fn = f1 + f2;
	        f1 = f2;
	        f2 = fn;
	    }
	    return fn;
	}
}