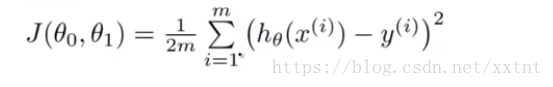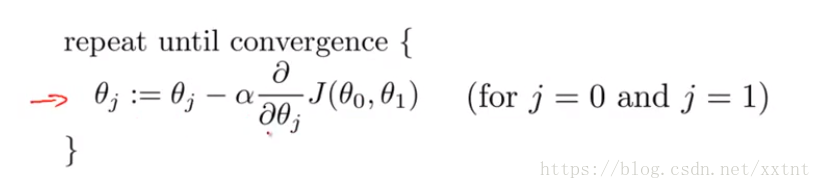吳恩達機器學習課程筆記02——處理房價預測問題(梯度下降演算法詳解)
建議記住的實用符號
| 符號 |
含義 |
| m |
樣本數目 |
| x |
輸入變數 |
| y |
輸出變數/目標變數 |
| (x,y) |
訓練樣本 |
| (x^(i),y^(i)) |
第i個訓練樣本 |
| h |
假設的函式( h(x) = y ) |
H函式:
h
備註:常用希臘字母
| Α α:阿爾法 Alpha |
Β β:貝塔 Beta |
Γ γ:伽瑪 Gamma |
Δ δ:德爾塔 Delte |
| Ε ε:艾普西龍 Epsilon |
Ζ ζ :捷塔 Zeta |
Ε η:依塔 Eta |
Θ θ:西塔 Theta |
| Ι ι:艾歐塔 Iota |
Κ κ:喀帕 Kappa |
∧ λ:拉姆達 Lambda |
Μ μ:繆 Mu |
| Ν ν:拗 Nu |
Ξ ξ:克西 Xi |
Ο ο:歐麥克輪 Omicron |
∏ π:派 Pi |
| Ρ ρ:柔 Rho |
∑ σ:西格瑪 Sigma |
Τ τ:套 Tau |
Υ υ:宇普西龍 Upsilon |
| Φ φ:fai Phi |
Χ χ:器 Chi |
Ψ ψ:普賽 Psi |
Ω ω:歐米伽 Omega |
1、已知訓練集
2、計算出恰當的θ0和θ1的值,使之得到的結果最接近已知的訓練集( hθ(x) = θ0 + θ1*x ),儘可能的讓其方差的1/2M的值最小。
代價函式(平方誤差函式): J(θ0, θ1) = 1/(2m)∑(h(x^(i) – y ^(i))²
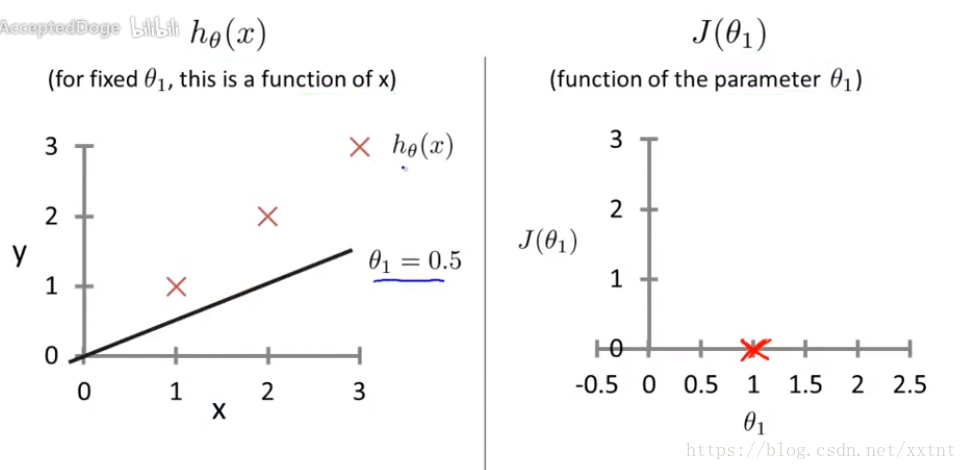
代價函式和假設函式
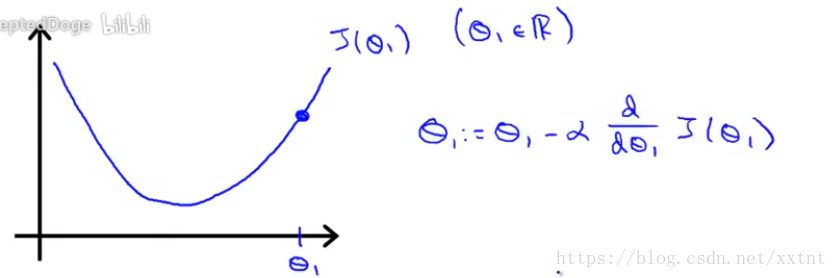
左邊是假設函式:假設函式是為了確定θ1的值,是一個關於x的函式
右邊是代價函式:是一個關於θ1的函式,求得不同θ1的情況下,代價函式的值(即誤差的大小)。
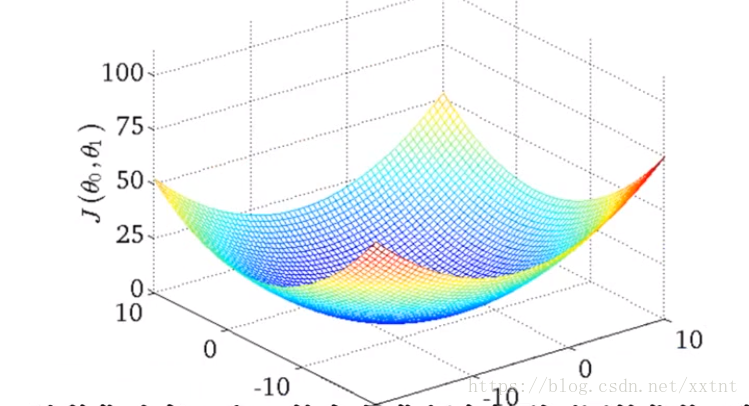
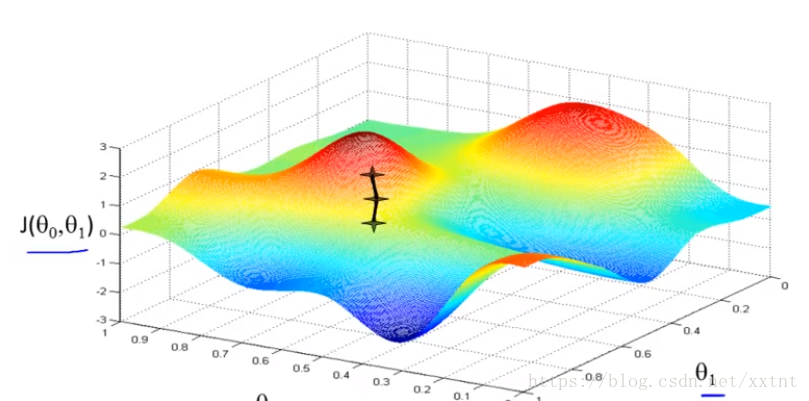
同時考慮θ0和θ1所繪製的代價函式,其中點最低的部分則是我們理想的假設函式。
求θ0和θ1的演算法
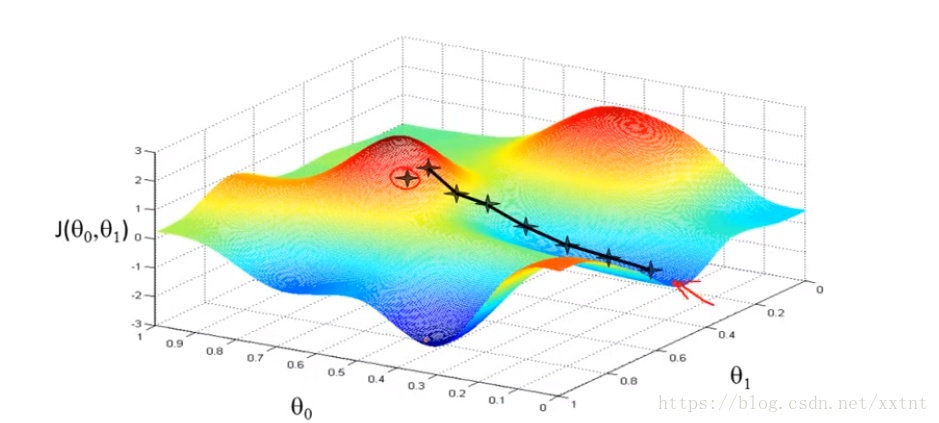
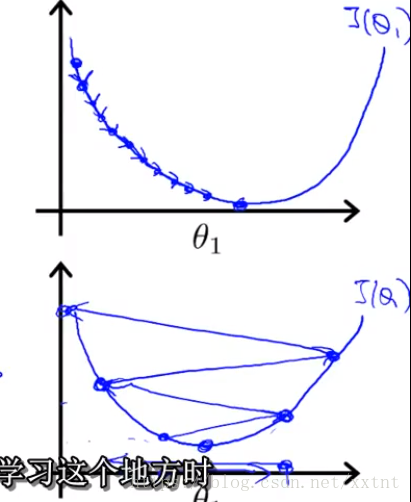
【梯度下降】將代價函式的值(就房價問題的訓練集)進行視覺化,想象如果你在山頂,以最快的速度走到山腳(即快速找到θ0和θ1恰當的值,使代價函式的值在某個較小的值的範圍內)
梯度下降函式會給我們返回區域性最優解,不同的初始值也許到達的點不同(即對θ0和θ1剛開始賦值不同,得到的最終值也會不一樣)
- 給θ0和θ1設定初始值
- 通過梯度下降演算法得到區域性最優解
梯度下降演算法
解析:
:= 賦值運算子(對的就是一個冒號加等號)
= 類似於C語言中的==(不知道老師使用的是哪裡的語法,matlab不是這樣的 [○・`Д´・ ○])
α 學習速率,是一個數字(控制下山的距離,即控制θ值變化的大小,其大小與α成正比,α>0 )
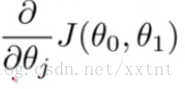
每一次都會重新對θ0和θ1重新賦值(同時更新,即兩個微分中的θ0和θ1都是它們原來的值)

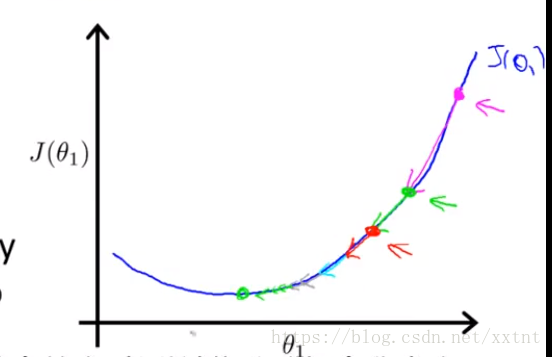
第二個它的導數值為正數,因為y值隨著x值的升高而升高
- 由於代價函式的值恆大於零(有其表示式可知),所以我們可以很容易得到,無論θ所在的斜率是正是負,它永遠是朝中J(θ)值降低的方向移動。因此,導數項的意義是為了保證隨著θ的變化是朝著代價函式的值下降的那個方向。
- α的值的大小也會影響到我們最終的結果,α值太小,會導致下降的比較慢,α太多,有可能會導致越過最低點。
如下圖
- 代價函式和導數的值同樣起到對下降距離的調節作用,隨著代價函式的值逐步降低,下降的距離逐漸變小,也就如下圖所示。
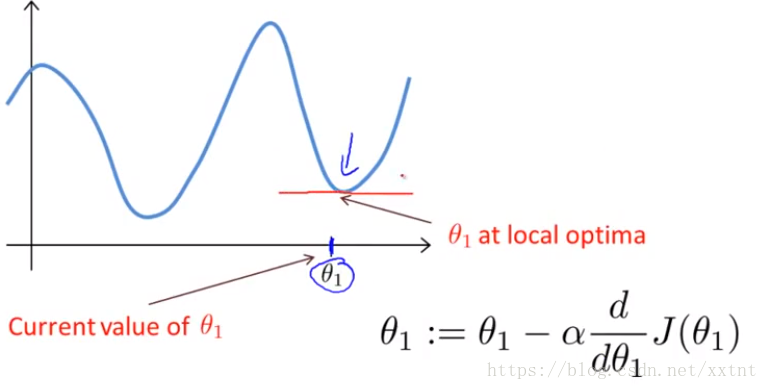
下降演算法的之所以存在區域性最優解,與其演算法有關。當到達一個位置θ0和θ1的偏導數都為0時,θ0和θ1將不再改變,也就是說,會出現求得的值為極小值而不是最小值的情況。(如果存在θ0和θ1都為0的多個點)
這也就是我們的梯度下降,其中圈著的部分,分別是各自偏導數求出的結果