斯坦福CS229機器學習課程筆記一:線性迴歸與梯度下降演算法
機器學習三要素
機器學習的三要素為:模型、策略、演算法。
策略:按照什麼樣的準則學習或選擇最優的模型。
最小化均方誤差,即所謂的 least-squares(在spss裡線性迴歸對應的模組就叫OLS即Ordinary Least Squares):
演算法:基於訓練資料集,根據學習策略,選擇最優模型的計算方法。
確定模型中每個θi取值的計算方法,往往歸結為最優化問題。對於線性迴歸,我們知道它是有解析解的,即正規方程 The normal equations:![]()
監督學習(Supervised Learning)
SupervisedLearning,Wiki
通過訓練資料(包含輸入和預期輸出的資料集)去學習或者建立一個函式模型,並依此模型推測新的例項。函式的輸出可以是一個連續的值(迴歸問題,Regression),或是預測一個分類標籤(分類問題,Classification)。
機器學習中與之對應還有:
無監督學習(Unsupervised Learning)
強化學習(Reinforcement Learning)

在課程中定義了一些符號:
x(i):輸入特徵(input features)
y(i) :目標變數(target variable)
(x(i),y(i)) :訓練樣本(training example)
{(x(i),y(i));i=1,...,m} :訓練集合(training set)
m :訓練樣本數量
h :假設函式(hypothesis)
線性迴歸(Linear Regression)
例子:房屋價格與居住面積和臥室數量的關係
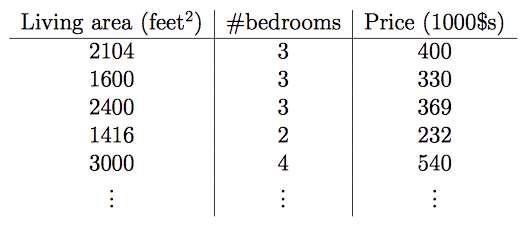
在這裡輸入特徵變成了兩個x1,x2,目標變數就是價格
x1: Living area
x2: bedrooms
可以把它們稱之為x的二維向量。
在實際情況中,我們需要根據你所選擇的特徵來進行一個專案的設計。
我們之前已經瞭解了監督學習,所以需要我們決定我們應該使用什麼樣的假設函式來進行訓練引數。線性函式是最初級,最簡單的選擇。
所以針對例子假設函式:
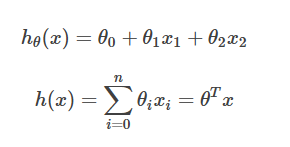
其中的θ就是要訓練的引數(也被成為權重),我們想要得到儘可能符合變化規律的引數,使得這個函式可以用來估計價格。
因為要訓練θ,所以引入cost function(損失函式/成本函式)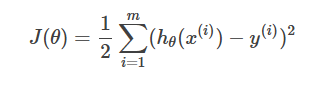
對於線性規劃問題,通常J函式(誤差平方和)是碗狀的,所以往往只會有一個全域性最優解,不用過多擔心演算法收斂到區域性最優解。
最小二乘法(LMS algorithm)
課程中的比喻很形象,將用最快的速度最小化損失函式 比作如何最快地下山。也就是每一步都應該往坡度最陡的方向往下走,而坡度最陡的方向就是損失函式相應的偏導數,因此演算法迭代的規則是:

其中α是演算法的引數learning rate,α越大每一步下降的幅度越大速度也會越快,但過大有可能導致演算法無法收斂。
假設只有一個訓練樣本:(x,
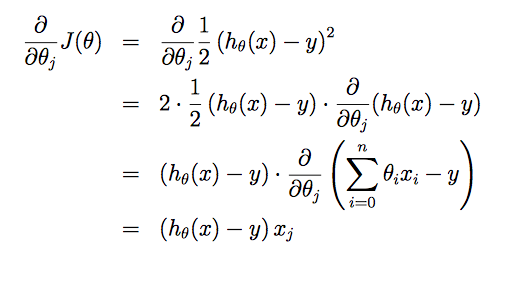
更新函式為:θj:=θj+α(y(i)−hθ(x(i)))x(i)j
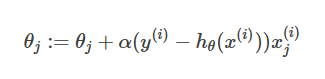
這就是最小二乘法(LMS, least mean squares)更新規則。
梯度下降(gradient descent)
在面對多個樣本進行處理時,就需要在此基礎上演變更新規則。有兩種策略:
批量梯度下降 batch gradient descent 
隨機梯度下降 stochastic gradient descent (incremental gradient descent) 
當訓練樣本量很大時,batch gradient descent的每一步都要遍歷整個訓練集,開銷極大;而stochastic gradient descent則只選取其中的一個樣本。因此訓練集很大時,後者的速度要快於前者。
雖然 stochastic gradient descent 可能最終不會收斂到最優解(代價函式等於0),大多數情況下都能得到真實最小值的一個足夠好的近似。
正規方程組(normal equations)
梯度的矩陣表示

針對矩陣中的每個元素對 f 求導,將導數寫在各個元素對應的位置。
矩陣的跡
一個 n×n 矩陣A的主對角線(從左上方至右下方的對角線)上各個元素的總和被稱為矩陣A的跡(或跡數),一般記作tr(A)。
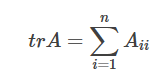

對Normal Equation求解

對J式子進行展開化簡
推倒過程利用了矩陣的跡的性質。因為J(θ)是個實數,所以它的跡等於它本身。

線性迴歸代價函式的選擇
為什麼在選擇策略J(θ)時,使用誤差h(x)-y的平方和。而不是其他代價函式?
線性迴歸的模型及假設:![]()
ε(i) ∼ N(0, σ2),隨機誤差ε服從正態分佈(Gaussian分佈)
ε(i) 是 IID的,即獨立同分布的
於是可以獲得目標變數的條件概率分佈:
整個訓練集的似然函式,與對數似然函式分別為:
因此,最大化對數似然函式,也就相當於最小化
區域性加權線性迴歸 (Locally weighted linear regression,LWR)
線上性迴歸中,使用某個訓練樣本 x 通過評價h(x)來更新 θ 時,其餘樣本對更新的貢獻是相同的;
在LWR中,使用某個訓練樣本 x 通過評價h(x)來更新 θ 時,離 x 近的點的重要性更高。
加權函式w的一個選擇是指數衰減函式,是一個鐘形 bell-shaped曲線,雖然長得像高斯分佈,但它不是高斯分佈:
|x(i) − x| 越小,距離越近,其權重w(i)越接近1; |x(i) − x|越大,則權重w(i)越小。
τ 被稱為bandwidth頻寬引數,控制 x(i) 的權重值隨著離 x 距離大小而下降的速率。τ越大,下降速度越慢
在調整 θ 的過程中。如果x(i) 權重大,要努力進行擬合 使誤差平方項最小。如果權重很小,誤差平方項將被忽略。
對新的 x 進行預測時,LWR和線性迴歸也有區別:
- LWR是一個非引數演算法 non-parametric algorithm:對每個新的 x 進行預測時,都需要利用訓練集重新做擬合,代價很高(因此有課上的學生質疑這是否稱得上是一個模型)。
- 線性迴歸是一個引數演算法:引數個數是有限的,擬合完引數後就可以不考慮訓練集,直接進行預測。
likelihood 和 probability的區別
probability 強調 y 發生的概率
likelihood 強調給定一組x,y。找到 θ 使 x 條件下 y 發生的機率最大。
參考:
https://blog.csdn.net/TRillionZxY1/article/details/76290919
https://www.cnblogs.com/logosxxw/p/4651231.html