計算機視覺(八):影象分割
一、閾值處理
由於閾值處理直觀、實現簡單且計算速度快,因此影象閾值處理在影象分割應用中處於核心地位。
1. 基礎知識
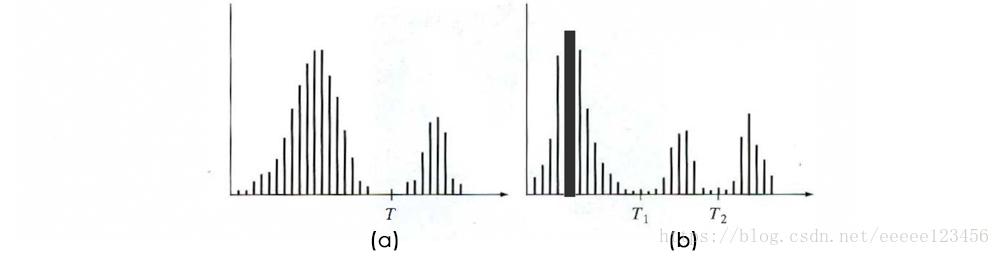
假設圖1(a)中的灰度直方圖對應於影象
,該影象由暗色背景上的較亮物體組成,以這樣的組成方式,物體畫素和背景畫素所具有的灰度值組成了兩種支配模式。從背景中提取物體的一種明顯方法是,選擇一個將這些模式分開的閾值
。然後,
的任何點
稱為一個物件點;否則該點稱為背景點。分割後的影象
由下式給出:
當
是一個適用於整個影象的常數時,上式給出的處理稱為全域性閾值處理。當
值在一幅影象上改變時,我們把該處理稱為可變閾值處理(區域性閾值處理或區域閾值處理有時用於表示可變閾值處理)。若
取決於空間座標
本身,則可變閾值處理通常稱為動態閾值處理或自適應閾值處理。
圖1(b)顯示了一個更為困難的閾值處理問題,它包含有三個支配模式的直方圖。分割的影象由下式給出:
式中,a、b和c是任意三個不同的灰度值。
2. 基本的全域性閾值處理
當物體和背景畫素的灰度分佈十分明顯時,可以用適用於整個影象的單個(全域性)閾值。能對每幅影象自動估計閾值的演算法如下:
① 為全域性閾值
選擇一個初始估計值。
② 在式(1)中用
分割該影象。這將產生兩組畫素:
由灰度值大於
的所有畫素組成,
由所有小於等於
的畫素組成。
③ 對
和
的畫素分別計算平均灰度值(均值)
和
。
④ 計算一個新的閾值:
⑤ 重複步驟2到步驟4,直到連續迭代中的
值間的差小於一個預定義的引數
為止。
通常,
越大,則演算法執行的迭代次數越少。所選的初始閾值必須大於影象中的最小灰度級而小於最大灰度級。影象的平均灰度對於
來說是較好的初始選擇。
3. 用Otsu方法的全域性閾值處理
令
表示一幅大小為
畫素的數字影象中的
個不同的灰度級,
表示灰度級為
的畫素數。影象中的畫素總數為
。歸一化的直方圖具有分量
。由此有
假設使用閾值把輸入影象處理為兩類
和
,Ostu演算法如下:
① 計算輸入影象的歸一化直方圖。使用