data(churn)匯入自帶的訓練集churnTrain和測試集churnTest

　　用id3、cart、C4.5和C5.0建立決策樹模型，並用交叉矩陣評估模型，針對churn資料，哪種模型更合適　　

　　決策樹模型 ID3/C4.5/CART演算法比較　　　傳送門

 

　　data(churn)為R自帶的訓練集，這個data(chun十分特殊)

　　先對data(churn)訓練集和測試集進行資料查詢

 

 churnTest資料

 

 

 

　　奇怪之處，不能儲存它的資料，不能檢視資料的維度 ，不能檢視資料框中每個變數的屬性！！

> data(churn)
> Gary<-data(churn)
> 
> dim(data(churn))
NULL
> dim(Gary)
NULL
> 
> str(data(churn))
 chr "churn"
> str(Gary)
 chr "churn"

 

 

 

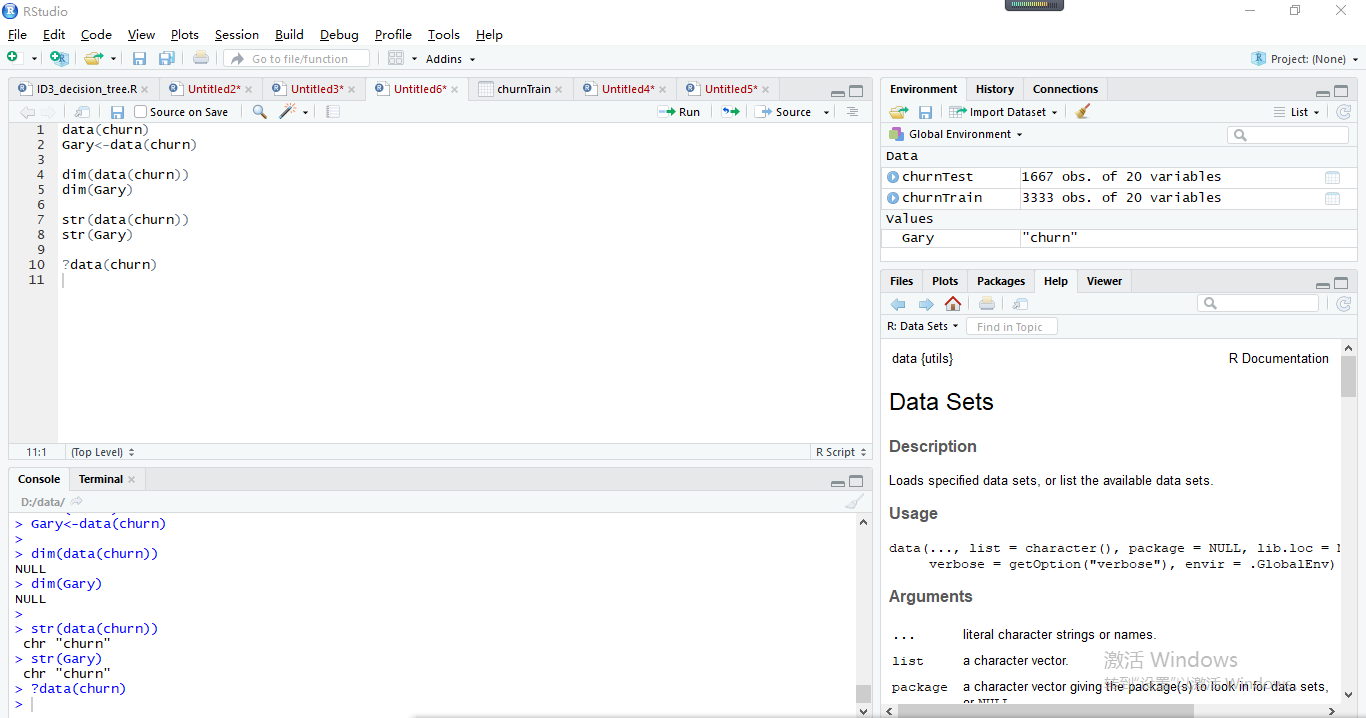
　　官方我只看懂了它是一個數據集：載入指定的資料集，或列出可用的資料集(英文文件真是硬傷∑=w=)

　　用不同決策樹模型去預測它churn資料集，比較一下哪種模型更合適churn資料

 

　　比較評估模型(預測)的正確率

#正確率
sum(diag(tab))/sum(tab)

 

id3建立決策樹模型

#載入資料
data(churn)

#隨機抽樣設定種子，種子是為了讓結果具有重複性
set.seed(1) 

library(rpart)

Gary1<-rpart(churn~.,data=churnTrain,method="class", control=rpart.control(minsplit=1),parms=list(split="information")) 
printcp(Gary1)

#交叉矩陣評估模型
pre1<-predict(Gary1,newdata=churnTrain,type='
 
class')
tab<-table(pre1,churnTrain$churn)
tab

#評估模型(預測)的正確率
sum(diag(tab))/sum(tab)

Gary1.Script

pre1   yes   no
  yes  360   27
  no   123 2823

> sum(diag(tab))/sum(tab)
[1] 0.9549955

 

cart建立決策樹模型

data(churn)

set.seed(1) 

library(rpart)

Gary1<-rpart(churn~.,data=churnTrain,method="class", control=rpart.control(minsplit=1),parms=list(split="gini"))  
printcp(Gary1)

#交叉矩陣評估模型
pre1<-predict(Gary1,newdata=churnTrain,type='class')
tab<-table(pre1,churnTrain$churn)
tab

#評估模型(預測)的正確率
sum(diag(tab))/sum(tab)

Gary2.Script

pre1   yes   no
  yes  354   35
  no   129 2815

> sum(diag(tab))/sum(tab)
[1] 0.9507951

 

C4.5建立決策樹模型

data(churn)

library(RWeka)

#oldpar=par(mar=c(3,3,1.5,1),mgp=c(1.5,0.5,0),cex=0.3)

Gary<-J48(churn~.,data=churnTrain)

tab<-table(churnTrain$churn,predict(Gary))
tab
#評估模型(預測)的正確率
sum(diag(tab))/sum(tab)

Gary3.Script

    
       yes   no
  yes  359  124
  no    24 2826

> sum(diag(tab))/sum(tab)
[1] 0.9555956

 

C5.0建立決策樹模型

data(churn)
treeModel <- C5.0(x = churnTrain[, -20], y = churnTrain$churn)

ruleModel <- C5.0(churn ~ ., data = churnTrain, rules = TRUE)

tab<-table(churnTest$churn,predict(ruleModel,churnTest))
tab
#評估模型(預測)的正確率
sum(diag(tab))/sum(tab)

Gary4.Script

     
       yes   no
  yes  149   75
  no    15 1428

> sum(diag(tab))/sum(tab)
[1] 0.9460108

 

 　　

 

 

實現過程

 

id3建立決策樹模型：

　　載入資料，隨機抽樣設定種子，種子是為了讓結果具有重複性

data(churn)

set.seed(1) 

 

　　使用rpart包建立決策樹模型

> Gary1<-rpart(churn~.,data=churnTrain,method="class", control=rpart.control(minsplit=1),parms=list(split="information")) 
> printcp(Gary1)

Classification tree:
rpart(formula = churn ~ ., data = churnTrain, method = "class", 
    parms = list(split = "information"), control = rpart.control(minsplit = 1))

Variables actually used in tree construction:
[1] international_plan            number_customer_service_calls state                        
[4] total_day_minutes             total_eve_minutes             total_intl_calls             
[7] total_intl_minutes            voice_mail_plan              

Root node error: 483/3333 = 0.14491　　　　　　#根節點錯誤：483/3333＝0.14491

n= 3333 

        CP nsplit rel error  xerror     xstd　　　　　　#錯誤的XSTD
1 0.089027      0   1.00000 1.00000 0.042076
2 0.084886      1   0.91097 0.95445 0.041265
3 0.078675      2   0.82609 0.90269 0.040304
4 0.052795      4   0.66874 0.72878 0.036736
5 0.022774      7   0.47412 0.51139 0.031310
6 0.017253      9   0.42857 0.49068 0.030719
7 0.012422     12   0.37681 0.46170 0.029865
8 0.010000     17   0.31056 0.43892 0.029171

 

　　交叉矩陣評估模型

> pre1<-predict(Gary1,newdata=churnTrain,type='class')
> tab<-table(pre1,churnTrain$churn)
> tab
     
pre1   yes   no
  yes  360   27
  no   123 2823

 

　　對角線上的資料實際值和預測值相同，非對角線上的值為預測錯誤的值

　　評估模型(預測)的正確率

> sum(diag(tab))/sum(tab)
[1] 0.9549955

 

　　　　diag(x = 1, nrow, ncol) 

　　　　diag(x) <- value 

　　解析： 

　　　　x：一個矩陣,向量或一維陣列,或不填寫。 

　　　　nrow, ncol：可選 行列。 

　　　　value ：對角線的值，可以是一個值或一個向量

diag()函式

 

 

cart建立決策樹模型：

　　與id3區別parms=list(split="gini")) 

Gary1<-rpart(churn~.,data=churnTrain,method="class", control=rpart.control(minsplit=1),parms=list(split="gini"))  

 

　　解釋略

> data(churn)
> 
> set.seed(1) 
> 
> library(rpart)
> 
> Gary1<-rpart(churn~.,data=churnTrain,method="class", control=rpart.control(minsplit=1),parms=list(split="gini"))  
> printcp(Gary1)

Classification tree:
rpart(formula = churn ~ ., data = churnTrain, method = "class", 
    parms = list(split = "gini"), control = rpart.control(minsplit = 1))

Variables actually used in tree construction:
[1] international_plan            number_customer_service_calls state                        
[4] total_day_minutes             total_eve_minutes             total_intl_calls             
[7] total_intl_minutes            voice_mail_plan              

Root node error: 483/3333 = 0.14491

n= 3333 

        CP nsplit rel error  xerror     xstd
1 0.089027      0   1.00000 1.00000 0.042076
2 0.084886      1   0.91097 0.96273 0.041414
3 0.078675      2   0.82609 0.90062 0.040265
4 0.052795      4   0.66874 0.72050 0.036551
5 0.023810      7   0.47412 0.49896 0.030957
6 0.017598      9   0.42650 0.53416 0.031942
7 0.014493     12   0.36853 0.51553 0.031426
8 0.010000     14   0.33954 0.48654 0.030599
> 
> #交叉矩陣評估模型
> pre1<-predict(Gary1,newdata=churnTrain,type='class')
> tab<-table(pre1,churnTrain$churn)
> tab
     
pre1   yes   no
  yes  354   35
  no   129 2815
> 
> #評估模型(預測)的正確率
> sum(diag(tab))/sum(tab)
[1] 0.9507951

 

 

C4.5建立決策樹模型：

　　讀取資料，載入party包

data(churn)

library(RWeka)

 

　　使用rpart包J48()建立決策樹模型

> Gary<-J48(churn~.,data=churnTrain)

> tab<-table(churnTrain$churn,predict(Gary))
> tab
     
       yes   no
  yes  359  124
  no    24 2826

> #評估模型(預測)的正確率
> sum(diag(tab))/sum(tab)
[1] 0.9555956

 

 

C5.0建立決策樹模型：

　　C5.0演算法則是C4.5演算法的商業版本，較C4.5演算法提高了運算效率，它加入了boosting演算法，使該演算法更加智慧化

　　解釋略

> data(churn)
> treeModel <- C5.0(x = churnTrain[, -20], y = churnTrain$churn)
> 
> ruleModel <- C5.0(churn ~ ., data = churnTrain, rules = TRUE)
> 
> tab<-table(churnTest$churn,predict(ruleModel,churnTest))
> tab
     
       yes   no
  yes  149   75
  no    15 1428
> #評估模型(預測)的正確率
> sum(diag(tab))/sum(tab)
[1] 0.9460108

 

diag(x = 1, nrow, ncol) 

　　　　diag(x) <- value 

　　解析： 

　　　　x：一個矩陣,向量或一維陣列,或不填寫。 

　　　　nrow, ncol：可選 行列。 

　　　　value ：對角線的值，可以是一個值或一個向量