決策樹的進化（ID3、C4.5、CART、GBDT、RF、DART、lambdaMART、XGBoost、lightGBM）
pipeline
在資料探勘領域中，決策樹是對資料進行建模的一種很有效的手段。當資料集被清洗好後，資料集就是樣本的集合，每一個樣本都是有一樣多的屬性，但屬性值可能不同（也有可能不存在即屬性值缺失）。每一個樣本，分為屬性（也可稱為特徵）和label兩部分，我們運用決策樹處理資料就是為了從樣本的這些屬性裡面找出規則，來建立模型可以去預測樣本中label，而樣本中的原label我們稱之為ground truth，與預測的label按一定的方式進行計算得出損失值，通過減小該損失值來優化模型。
決策樹
決策樹首先是一棵樹，樹含有一個根結點、若干個內部結點及若干個葉結點。這樣的一棵樹其實就對應了一種決策規則，對於新的樣本，我們根據它的屬性，從根結點向下開始逐步進行屬性測試，最終葉結點對應決策結果。下面來說說具體的建樹過程：
給定輸入訓練集，訓練集中每一個樣本含x和y，x就是樣本的屬性部分，y就是label，A是x中所含屬性的集合。舉個例子，假定某資料集用來記錄人體體質是否達標的，那麼用到的指標（屬性）可以是身高、體重、年齡，A={身高，體重，年齡}，D中的x可以是（180，64，25）（這就是屬性值），y可以是達標或不達標（可以用布林變數0，1表示）。
從上圖可以看出，決策樹演算法是一個遞迴的過程。首先生成第一個結點，該結點為根結點，包含所有的樣本和所有的屬性，直接對結點進行遞迴邊界測試，一是看該結點所包含的樣本是不是都屬於同一個label，是就直接返回，該結點作為葉結點，該label就是該葉結點的預測label。如果不是第一種情況，那麼再看屬性集是不是為空，或者該結點所包含的所有樣本是不是在屬性集上都屬於同一個label，是則返回，否則的話就要選取最優屬性進行劃分。假定按照某種方式
通俗點講，就是給定一個集合和一些判斷點，把集合按照這些判斷點用if-else-elif的形式不斷進行劃分，當到達遞迴邊界時就停止劃分，並給出葉結點的預測label。那麼我們所建立的決策樹模型實際上就是一個龐大的if-else語句的塊，在新樣本到來時，我們還是根據新樣本的所有屬性的屬性值情況，用if-else對它不斷進行判別，最終流到葉結點，該葉結點的預測label就是新樣本的預測label，我們得到的決策樹就是類似if-else-elif的語句塊。
ID3（Iterative Dichotomiser）
在上文中描述的某種方式就是本節所要討論的內容，也就是最優屬性的選擇問題。首先我們來解決為什麼要選取最優屬性的問題，然後解決如何選取最優屬性的問題。
在對訓練集進行劃分後，得到的進一步的模型是要比未劃分的模型更準確，因為劃分之後結點的純度（樣本子集中屬於同一label的比例）就會提高，這樣就能提高預測新樣本的準確率。但是我們是想要得到最優的屬性，然後將樣本集合按照這個屬性劃分時，純度的提升會更多些。
對於純度的提升大小，我們可以用資訊增益來表示，那麼選擇最優屬性其實就是選擇使得資訊增益最大的那個屬性。而某屬性的資訊增益是由按照該屬性劃分前後的資訊熵之間的差表示的，資訊熵定義為：
D是樣本集合，|y|是label種類的個數，y是label的種類集合，pk是當前樣本集合D中第k類樣本所佔的比例。
那麼資訊增益的計算就可以由下面的公式來表示：
被減數就是劃分前的資訊熵，減數則是按某屬性劃分後的各分支下的資訊熵之和，那麼兩個值相減就得到了資訊增益。資訊熵衡量了當前資料集的混亂程度，資訊熵越大則說明混亂程度越大，純度越低。但我們是想要純度越低越好，那麼也就是減數越小越好，這樣也就對應了資訊增益越大越好。
ID3就是以資訊增益為指標來選取最優劃分屬性的，但是仍有不足。也就是，它傾向於選取取值數目多的屬性，因為這樣的屬性計算出來的資訊增益最大，但往往會導致泛化能力變弱。比如樣本集有100個樣本，然後樣本有一個編號屬性，100個樣本的編號各不相同，如果按編號屬性劃分則對新樣本的預測很不友好，因為編號對label的影響太小了。
基於此，下面就有C4.5的最優屬性選取方式就減輕了資訊增益的傾向帶來的不足。
C4.5
C4.5採用增益率來選取最優屬性，也就是在ID3提出的資訊增益下面加一個分母，這個分母就是用來懲罰取值數目過多的屬性。以下就是增益率的定義：
IV(a)稱為屬性a的固有值，如果屬性a的取值數目過多，那麼IV(a)會變得很大，那麼增益率就會變得很小。但是C4.5並不是單純地選取增益率最大的屬性作為最優屬性，而是先比較資訊增益，也就是說我們在資訊增益高於平均水平的屬性集合中再選取增益率最大的屬性。
CART（Classification and Regression Tree）
CART決策樹使用基尼指數來衡量資料集的純度，基尼指數越小，資料集的純度就越高，可以基尼指數類比為資訊熵。但事實上，基尼指數是反映從資料集中隨機抽取兩個樣本，label不一致的概率。對於這個概率，我們希望它越小越好，這樣資料集的純度就越高。基尼指數的定義如下：
類比4.2公式的減數的形式，我們可以得到屬性a的基尼指數定義為：
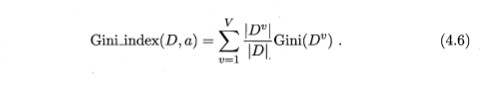
根據上式，我們依次計算各屬性的基尼指數，然後將基尼指數最大的屬性作為最優屬性。
GBDT（MART、GBRT、GBM）
上文敘述的ID3、C4.5、CART的內容主要是針對分類樹最優屬性的選取方法的介紹，從這節開始介紹針對迴歸樹最優屬性的選取方法以及怎樣從決策樹本身的模型改進。
GBDT（梯度提升樹）是由Boosting Tree（提升樹）改進而來，直接先擺上提升樹的演算法偽碼：
我們知道一棵樹的預測結果是由樹的葉子結點給出的，提升樹的預測結果是一系列迴歸樹的預測結果之和。那麼構建提升樹就由構建第一顆迴歸樹開始，先初始化提升樹模型f0(x)=0，也就是該提升樹對所有的x的預測label都是0。然後計算殘差，也就是用ground truth減去預測label，擬合得到的新資料集（x，r）就得到第一棵迴歸樹T。
迴歸樹的生成其實與前文所述的分類樹的生成相似，不同之處在於選取最優屬性的優化目標不同。分類樹的優化目標就是資訊增益，增益率以及基尼指數等，而回歸樹的優化目標（這裡用的損失函式是MSE）如下：
首先遍歷資料集的屬性集，對於每一個屬性j，我們優化上述目標。由於屬性j有很多取值，那麼從這些取值中先計算劃分點，一般是相鄰兩個值的中間數作為劃分點，這樣我們的到劃分點s的集合。舉個例子，假如j有10個取值，那麼先從小到大排序，然後可以計算10個取值中的劃分點，相鄰兩個取值的平均值作為一個劃分點，我們就可以得到9個劃分點。
上述優化目標也就是，遍歷每一個可能的j和s，尋找使得上述目標最小的j，s來劃分當前結點。其中c1、c2是各分支的預測label（一般取分支結點的資料集的均值），R1、R2是各分支的樣本子集。注意這裡是用CART迴歸樹舉例，對於結點的劃分只能產生兩個分支。劃分之後，遞迴地對子結點利用上述優化目標進行劃分，直至到達遞迴邊界（一般是限定葉子個數，最大深度等）。
得到這樣的迴歸樹之後，我們利用步驟(c)更新提升樹的模型fm，並再次計算殘差，又得到新的資料集（x，r），繼續擬合生成新的迴歸樹直至迭代到M。
下面我們進入正題，GBDT在BT上的改進之處是，初始化的f0(x)如下所示：
L是自己選的損失函式，若取MSE則c是label的均值。殘差則變為：
m是指第m棵迴歸樹，f是提升樹模型，xi、yi則是資料集中的樣本。這樣，之前的簡單作差就變為負梯度，我們將x與負梯度組合成新的資料集，用迴歸樹去擬合，然後更新提升樹的模型，這就是GBDT。
RF（Random Forest）
上文中GBDT是代表了Boosting這個整合方法，也就是利用負梯度一點點優化提升模型，只能序列計算。而此節要介紹的隨機森林是代表了Bagging這個整合學習方法，可以平行計算。
首先直接擺上Bagging演算法的偽碼：
自主取樣也就是bootstrap sampling，假定資料集含有m個樣本，那麼從該資料集中有放回地隨機取m次，最終還是得到了含有m個樣本的資料集，但是樣本分佈變了，也就是說有的樣本可能重複了好幾次，有的樣本可能沒有。
那麼對於這樣的資料集，我們總共生成T個，然後用基學習器去擬合數據集。當各個基學習器訓練好後，對於新樣本，我們用每個基學習器對其預測label，如果是分類就用服從多數的策略決定最終最終的預測label，如果是迴歸就用平均或加權平均（賦予基學習器權重）等策略。
RF則是以決策樹為基學習器，以Bagging為基礎，但是還增加了隨機選取屬性的特點。也就是，對於每個生成的隨機樣本集，我們還限制屬性集，只取其中的一部分屬性。假設總共有d個屬性，推薦選取k=log(d)為屬性子集的元素個數（log底數為2）。
DART（Dropouts meet Multiple Additive Regression Trees）
DART利用了深度神經網路中dropout設定的技巧，隨機丟棄生成的決策樹，然後再從剩下的決策樹集中迭代優化提升樹，這是DART的主要思想。下面直接上演算法偽碼來說DART與GBDT（MART）的不同之處和DART的原理：
剛開始時，還是初始化提升樹模型為f0(x)=0，然後根據損失函式計算負梯度，並生成中間資料集，也就是S1，之後再利用迴歸樹訓練中間資料集得到T1，加入集合M中。
下面進入dropout環節，對M中的每棵樹以Pdrop機率決定其是否被丟棄，若都不被丟棄，那麼等概率隨機選一棵。我們將丟棄的樹加入集合D中，未被丟棄的樹加入M帽中。
對於M帽中的樹，我們按照傳統GBDT的做法進行迭代更新，但是生成的新樹需要被乘上一個正則化因子1/(|D|+1)。因為不丟棄樹併產生新樹時，我們迭代更新出來的提升樹是被多迭代了|D|+1次負梯度，為了抵消這個差距，就需要正則化這一步。那麼對於被丟棄的樹，我們乘上|D|/(|D|+1)來統一數量級。
之後仍是隨機丟棄樹產生D，並在剩樹的集合中進行GBDT中的做法。這樣一看，當我們不丟棄任何樹時，其實就是傳統的GBDT，而丟棄所有樹時就相當於RF，因為每次都得重新生成迴歸樹，並沒有之前的迴歸樹作為基礎。
lambdaMART
要介紹lambdaMART，我們就得先從RankNet說起。RankNet的實現既可以用神經網路來實現，也可以用決策樹實現，總之它是將一個輸入向量對映成一個實數。具體說來，給定一個數據集，而資料集是根據不同的query來劃分的，對於每一個query，會有許多doc（查詢的結果比如url等），這些doc自身的好壞我們不清楚，但是doc pair內與query誰更相關是已知的，這其實就是pair-wise。那麼RankNet所做的就是將doc所轉換成的feature對映成一個實數（其實就是對這個doc打分），也就是s = f(x)，x就是doc feature，f是RankNet，s是分數。根據各個doc的分數，我們可以算出doc pair內一種偏序概率，如下所示：
（1）
Ui、Uj代表doc pair內的兩個doc，這個Pij指的是Ui相比Uj對於query來說更相關的概率，Ui|>Uj指Ui比Uj更相關，Si、Sj指的是兩個doc對應的分數，σ是該logistic函式的係數，自己指定一個就行。Pij只是通過分數S算出來的概率，是RankNet預測的結果，我們通過這個算出來的概率來計算損失，如下所示:
（2）
其中Pij帽指的是真實概率，假設Sij只能取0，1，-1三者之一，在doc i比doc j更相關時，Sij = 1，反之，Sij = -1，相等則為0，那麼Pij帽 = (1/2)*(1+Sij)，那麼聯合上述兩式我們可以得到：
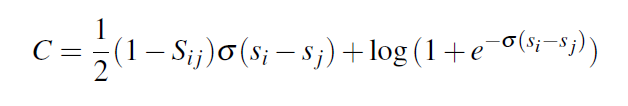（3）
根據（1），我們可以得到Pij是（Si-Sj）的增函式（σ取正實數），也就是Si越比Sj大，就說明Pij越接近1。
所以當Sij = 1時，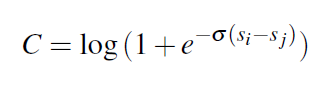
那麼Pij越接近1則C越小，也就是說明預測得還行。
當Sij = -1時，
那麼Pji越接近1則C越小，也就是說明預測得還行。
而Si = Sj時，C = log2，當RankNet分辨不出來哪個更相關時，還是會有懲罰，也就是想要RankNet被訓練得更魯棒。
而我們用梯度下降法更新RankNet的權重時，下述導數得用到：
（4）
假設Wk為模型的引數，η為學習率，那麼由隨機梯度下降法得到：
（5）
若是用MART實現RankNet，則是直接計算(4)左式的相反數，然後與輸入x生成中間資料集。
*************************************************************************************************************************************************
通過對梯度的因式分解，我們可以得到：
（6）
那麼：
（7）
其中C = C（Si-Sj），這個不是C與（Si -Sj）相乘，而是表示函式控制代碼。
對於（5）中減數，我們通過（6）得到：
其中：
只是統一下符號，便於合併同類項。
其中I是doc pair{i，j}的集合，假設集合I中的doc pair是{Ui，Uj}並且Ui總是比Uj更相關，那麼Sij總是等於1。我們在原來的λij後面乘上一個評價變化的因子，這樣一變經實驗驗證效果更好，這個|△NDCG|是交換Ui，Uj的位置引起的NDCG指標的變化值，有如下式子:
這樣我們改變了梯度的意義，之前我們優化目標是減小損失C，現在是增大NDCG的值，因為NDCG越大說明效果越好，我直接貼上NDCG的定義：
上述介紹其實就是lambdaRank，對RankNet做了兩點改進，一是因式分解加速了訓練，二就是|△NDCG|的引入。
*************************************************************************************************************************************************
lambdaMART與GBDT的不同之處在於將殘差換為了λ，也就是說對每個樣本（doc i），我們都求出它的λ，這個就是梯度，然後後面跟GBDT的演算法基本一致，只不過加了二次優化。
XGBoost
首先回顧GBDT，它的大體流程如下：
其中求w也就是根據最小化損失函式求j、s，也就是最優屬性及最優切分點，步長在上圖中其實是shrinkage，原始GBDT直接是預設為1。GBDT是直接對損失函式L求負梯度作為預測值，就是上圖中所示的2.1步，而XGBoost則對損失函式進行了二階求導，如下圖所示：
後面的Ω是正則化項，如下圖所示：95
然後我們直接讓目標函式的導數為0，求得下圖中的（5），（6）是代入w後的損失函式，w其實就是葉結點的預測值以及權重：
我們還可以利用目標函式確定最優屬性和最佳切分點，如下圖所示：
然後其他的就與GBDT相同了，XGBoost實際上就是在GBDT基礎上加了二次優化和正則項。
lightGBM
lightGBM主要是利用了大梯度單邊取樣、互斥特徵繫結、直方圖演算法、leaf-wise策略等技巧使得訓練速度大幅提升，記憶體消耗大量減少。下面分別介紹下這幾個技巧。
大梯度單邊取樣：
對資料集中每個樣本計算梯度，然後按降序排序，取前a*100%的樣本作為大梯度子集，在剩下的樣本（1-a）中隨機取b*100%個樣本作為小梯度子集，然後乘上（1-a）/b以保持資料分佈不變，最後合併大梯度子集和小梯度子集作為新的訓練集去訓練決策樹，在每次生成新樹時都進行上述取樣過程。
互斥特徵繫結：
由於許多高維度的資料都是比較稀疏的，也就是含有許多0，那麼進行特徵繫結就可以減少特徵的數量。舉例說明，樣本x含有10個特徵，特徵集是{a1,a2,...,a10}，我們發現a1與a2取值互斥，也就是很少同時取非零值，假設a1取值範圍為0~10，a2取值範圍為0~20，而且它們不同時取非零值，那麼對a2加一個偏置將其範圍變為10~30，這樣一來就可以將a1和a2兩個特徵捆綁起來，統一為一個特徵a12，它的取值範圍為0~30，x的特徵數量就從10個變為9個了。
直方圖演算法：
將特徵值離散化成k個整數，也就是k個bin的取值，然後將所有樣本點它的該特徵的取值情況選擇bin，並統計bin中所含樣本點個數。舉例說明，有三個樣本，分別為x1（0.1,1.1），x2（1.1,2.1），x3（0.2,3.1），首先將特徵離散化，第一維的特徵離散化成3個整數0、1、2，第二維的特徵離散化成3個整數1、2、3，那麼形成的直方圖就是bin1[0] = 2，bin1[1] = 1，bin1[2] = 0，bin2[1] = 1，bin2[2] = 1，bin2[3] = 1。尋找最優屬性和最佳切分點也是根據直方圖來確定的，這樣只需要掃描一次全部資料就能生成直方圖，而GBDT和XGBoost每次尋找劃分點時都要掃描全部的資料。
leaf-wise策略：
而XGBoost中則是這樣的：
前者比後者會減少更多的loss，但是複雜度較高容易過擬合，但可以通過設定max-depth引數來克服。
lightGBM是可以基於GBDT的，也就是說計算葉子結點的預測值是可以通過GBDT的方式進行的，當然也可以用牛頓法（XGBoost）。
上述是我近期對決策樹的一個總結，可能會有些錯誤，如有不清楚的地方和錯誤，請及時與我溝通。
主要參考文獻：
1.《機器學習》 周志華
2.《統計學習方法》李航
3. From RankNet to LambdaRank to LambdaMART: An Overview Christopher J.C. Burges
4.LightGBM: A Highly Efficient Gradient Boosting Decision Tree
5.DART: Dropouts meet Multiple Additive Regression Trees