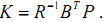最優控制(泛函)
LQR (linear quadratic regulator)即線性二次型調節器,其物件是現代控制理論中以狀態空間形式給出的線性系統,而目標函式為物件狀態和控制輸入的二次型函式。
LQR 的直觀推導及簡單應用 https://blog.csdn.net/heyijia0327/article/details/39270597
LQR控制器是怎麼計算反饋矩陣K的: 1.選擇引數矩陣Q,R 2.求解Riccati 方程得到矩陣P 3.計算
最優控制理論總結——動態規劃 https://blog.csdn.net/u014157632/article/details/53313109
最優控制 在滿足一定約束的情況下,尋求最優控制策略,使得效能指標取極大值或極小值 對一個受控的動力學系統,從一類允許的控制方案中尋找一個最優的控制方案,使得系統的運動從由某個初始狀態轉移到目標狀態的同時,其效能指標值為最優
性質 在一般的情況下,由極大值原理算出的最優控制是時間t的函式u(t),稱為程式控制或者開環控制稱為程式控制或者開環控制程式控制的主要缺點,是不能消除或者抑制由於引數的變動和環境的變化對系統造成的擾動,也就是魯棒性很差 最優控制的另一種形式是表示為狀態變數x(t)的函式u(x),實際上一種狀態反饋,稱為綜合控制或者閉環控制,其優點是能有效抑制擾動
解決方法
最優控制本質是變分問題,經典變分理論只能解決一類簡單的最優控制問題
現代變分理論最常用的就是極大值原理和動態規劃
按照控制作用實現方法分類,有開環最優控制和閉環最優
古典變分法研究對泛函求極值的一種數學方法,只能用在控制變數的取值範圍不受限的情況
極大值原理(龐特里亞金)是分析力學中哈密爾頓方法的推廣,其突出的優點是可以用於控制變數受限的情況
動態規劃(貝爾曼)其為數學規劃的一種,同樣可用於控制變數受限的情況,是一種適合於在計算機上進行計算的比較有效的方法
最優化方法(也稱做運籌學方法)是近幾十年形成的,它主要運用數學方法研究各種系統的優化途徑及方案,為決策者提供科學決策的依據。最優化方法的主要研究物件是各種有組織系統的管理問題及其生產經營活動。最優化方法的目的在於針對所研究的系統,求得一個合理運用人力、物力和財力的最佳方案,發揮和提高系統的效能及效益,最終達到系統的最優目標。
主要分支
線性規劃
當目標函式f是線性函式而且集合A是由線性等式函式和線性不等式函式來確定的, 我們稱這一類問題為線性規劃
整數規劃
當線性規劃問題的部分或所有的變數侷限於整數值時, 我們稱這一類問題為整數規劃問題
二次規劃
目標函式是二次函式,而且集合A必須是由線性等式函式和線性不等式函式來確定的。
非線性規劃
研究的是目標函式或是限制函式中含有非線性函式的問題。
隨機規劃
研究的是某些變數是隨機變數的問題。
動態規劃
研究的是最優策略基於將問題分解成若干個較小的子問題的優化問題。
組合最優化
研究的是可行解是離散或是可轉化為離散的問題。
無限維最優化
研究的是可行解的集合是無限維空間的子集的問題,一個無限維空間的例子是函式空間