PointNet學習筆記

本文記錄了博主在學習《PointNet: Deep Learning on Point Sets for 3D Clasification and Segmentation》過程中的總結筆記。更新於2018.10.12。

文章目錄

• PointNet學習筆記
• Introduction
• 問題描述
• Deep Learning on Point Sets
• 點雲資料的性質
• PointNet網路結構
• 理論分析
• 支撐材料C
• PointNet分類網路
• PointNet分割網路
• 基準3D CNN分割網路

Introduction

網路輸入：點雲輸據（point clouds）；
網路輸出：將輸入視作一個整體的標籤，或輸入內每個分割部分（segment/part）的標籤。

每個點的基本描述是其座標 $(x,y,$

網路的前一部分學習的是提取興趣點或資訊點，並將選擇它們的原因形成編碼；後面的全連線層則用於整合這些資訊，實現分類或分割。

另外，由於網路的輸入是點雲資料（每個點之間是獨立的），因此可以嘗試用一個空間轉換器（spatial transformer network）規範化資料。

論文中證明了所提網路可以模擬任何連續函式。通過實驗發現，網路會用一組稀疏的關鍵點總結描述輸入點雲，視覺化後發現，這些點恰巧也是目標圖形的骨架（skeleton）。

此外，論文中也從插點（outliers）和刪點（missing data）的角度證明了為何網路對於輸入的小擾動魯棒。

網路對於形狀分類、部分分割、場景分割等任務（資料庫下）都有較好的表現。

問題描述

用 $\{P_i\vert i=1,\cdot\cdot\cdot,n\}$描述一個3D點雲，其中每一個點 $P_i$都是一個向量。在本文中，除非特殊描述，其通道只包括位置資訊 $(x,y,z)$。

對於分類問題，網路輸出對應 $k$個類別的 $k$個概率；對於分割問題，網路則輸出所有 $n$個點對於所有 $m$個語義類別的的概率，即輸出尺寸為 $n\times m$。

Deep Learning on Point Sets

網路結構的提出是受到了 $\mathbb R^n$內點雲的性質的啟發，因此第一部分介紹性質，第二部分介紹網路結構。

點雲資料的性質

網路的輸入是歐氏空間下的一個點的子集，因此具有下面三個主要性質：

• 無序性（Unordered）：與畫素點陣或三維點陣下排布的網格狀資料不同，此時的點雲是無序的。因此要求一個以 $N$個3D點為輸入的網路需要對資料的 $N!$排布具有不變性（invariant to $N!$ permutations of the input set in data feeding order）。
• 點之間有關係（interaction among points）：由於這些點是空間中一個有意義的子集裡面按照某種距離矩陣生成的，這就要求網路要有能力識別這些相鄰點之間的區域性結構和這些結構的組合。
• 平移不變性（invariance under transformations）：習得的點雲描述應當對於某些變換魯棒，比如在點雲整體平移和旋轉等變換下，網路對於點雲的分割和分類結果不應當改變。

PointNet網路結構

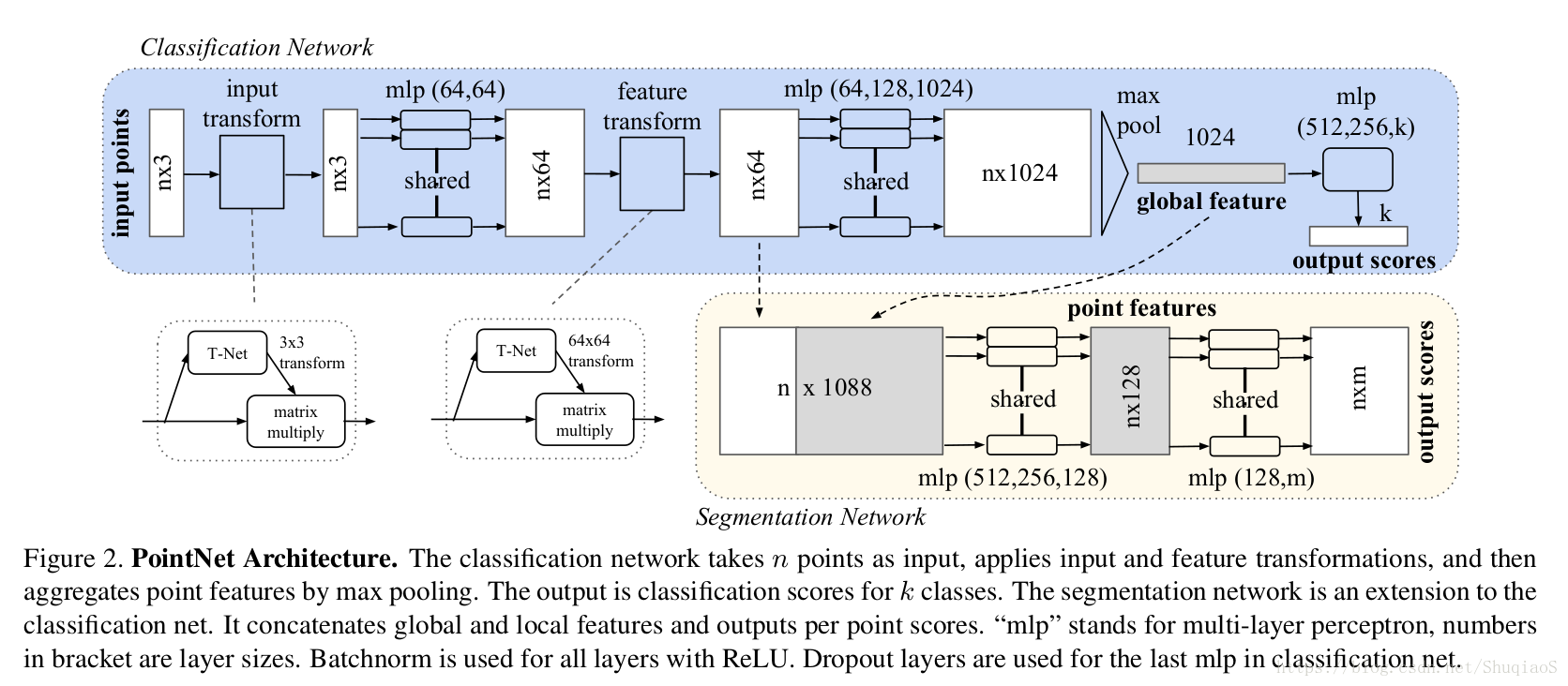
下圖是網路的整體結構（分割和分類網路共享大部分網路），包括用於整合所有點資訊的對稱函式max pooling、一個區域性和全域性資訊整合結構，和兩個連結結構用於連結輸入點和點特徵。

Symmetry Function for Unordered Input

目前存在三種方法保證模型對於輸入不同排序具有不變性：

1. 將輸入歸類為一個規範化的順序（canonical order）；
2. 在訓練RNN時將資料視為一個序列，但對訓練資料以所有可能的排序進行擴張；
3. 應用一個簡單的對稱函式整合每個點的資訊：此時，對稱函式以 $n$個向量為輸入，輸出一個對於輸入順序具有不變性的新向量（例如+和*操作都屬於二值對稱函式symmetric binary function）。

儘管第一種方法看起來很簡單，但實際上不難證明是無法找到一種高維下的排序使得其對於擾動魯棒的。這種方法比直接用無序輸入會稍微好一點，但表現還是很差。此外，對於第二種方法，儘管其對於小長度（幾十）的序列具有魯棒性，但對於上千個點（點雲的通常大小）就無法得到相同的表現了。文中的實驗證明了PointNet所使用的方法更好。

文中希望通過對變換後的元素應用對稱函式，從而估計得到一個定義在點集上的一般函式（general function）：
$f(\{x_1,\cdot\cdot\cdot,x_n\}) \approx g(h(x_1),\cdot\cdot\cdot,h(x_n)) \tag{1}$
其中， $f:x^{\mathbb R^N} \to \mathbb R$， $h: \mathbb R^N \to \mathbb R^K$，對稱函式 $g:\underbrace {\mathbb R^K \times \cdot \cdot\cdot\times \mathbb R^K}_n\to \mathbb R$ 。

文章通過實驗確定的基本模型用多層感知機（multi-layer perceptron）習得 $h$，用一個單變數函式（single variable function）和max pooling函式習得 $g$。通過不同的 $h$，可以習得表徵不同屬性的多個 $f$。

博主注：

1. 所謂多個 $f$：這裡的理解就像當一組點具有某種不同屬性時，其組成的整體也可以根據這些屬性得到可能的屬性。如大部分的點都是黑的，那麼整體的顏色屬性就是黑色；再如點與點之間存在某種位置關係，那麼整體就是球形；以此類推……。而這裡的 $f$就代表了不同考量下得到的屬性結論，而 $g$要近似的也是這種結論，只不過 $g$並非直接考量輸入的各個點，而是這些點經過 $h$處理後的體現。這就使得不同的 $h$處理出來經過相同的考量，也會對應不同的屬性結論，即不同的 $f$。
2. 為什麼可以有這個近似：因為如果直接以原始點為輸入，那麼對於點的排序就有要求。而通過之前的分析，是很難找到一種方法使得結果不受順序的影響。而這裡用於近似的函式 $g$是一個對稱函式，也就是其不考慮輸入的順序，只要保證需要的輸入都進來了，就可以了。然而，在原始特徵空間下，這種不考慮順序的行為是無法實現的，因此需要一種對映，將原始資料對映到一個新的空間，使得在該空間下，資料的順序（相互之間的關係）已經以某種形式表徵出來，從而使得接下來的操作不需要考慮順序。

區域性和全域性資訊整合（Local and Global Information Aggregation）

上面一步的輸出是一個表徵了全域性特徵的向量 $[f_1,\cdot\cdot\cdot,f_K]$。對於分類問題，可以直接訓練一個SVM或多層感知機分類器，用於在給定全域性特徵向量的基礎上判斷類別（比如黑色、球體等等得到“眼睛”）；但是對於點的分割問題，就需要統籌考慮全域性和區域性特徵了。文章的做法是將獲得的全域性特徵級聯在每個點的區域性特徵後面（如上圖中分割部分所示），在此基礎上再學習得到新的點區域性特徵，此時的每個點的特徵就既包含區域性特徵（區域性幾何資訊）又包含全域性特徵（全域性語義）了。

Joint Alignment network

一個點雲的語義標籤應當對於部分變換（如剛體變換rigid transformation）具有不變性。因此，應當要求習得的點雲描述也對於這些變換具有不變性。

一個比較典型的做法是在提取特徵之前將所有輸入集合整合到一個標準化空間（canonical space）內。與之前存在的工作（原文參考文獻9）不同，文章中的做法不需要發明任何新的層，也不需要引入任何別名（alias）。論文中應用了一個迷你網路T-Net學習一個仿射變換，並將其直接應用到原始點雲座標系。

T-Net是作為整個網路的一部分存在的，其中包括點獨立特徵提取（point independent feature extraction）、max pooling、和全連線層。關於T-Net的詳細資訊可以看支撐材料的學習。

同樣的思想也可以用於特徵空間，即用於整合不同點雲得到的特徵。然而，由於特徵空間下的變換矩陣維度要遠遠高於原始空間，為了降低最優化的難度，文章作者在softmax訓練損失的基礎上加了一個正則項：
$L_{reg}=\Vert I-AA^T\Vert _F^2$
其中 $A$是迷你網路習得的特徵整合矩陣。該正則項要求學習得到的矩陣是正交矩陣，因為正交變換不會丟失輸入的資訊。

理論分析

1. 萬能近似（Universal approximation）

博主注：雖然神經網路的主要運算層進行的都是線性運算，但我們無需為了期望的到的非線性函式單獨設計需要的模型。萬能近似定理（Universal approximation theorem）(Hornik et al., 1989;Cybenko, 1989) 表明，一個前饋神經網路如果具有線性輸出層和至少一層具有任何一種‘‘擠壓’’ 性質的啟用函式（例如logistic sigmoid啟用函式）的隱藏層，只要給予網路足夠數量的隱藏單元，它可以以任意的精度來近似任何從一個有限維空間到另一個有限維空間的Borel 可測函式。
萬能近似定理意味著無論我們試圖學習什麼函式，我們知道一個大的MLP 一定能夠表示這個函式。然而，我們不能保證訓練演算法能夠學得這個函式。即使MLP能夠表示該函式，學習也可能因兩個不同的原因而失敗。

• 用於訓練的優化演算法可能找不到用於期望函式的引數值。
• 訓練演算法可能由於過擬合而選擇了錯誤的函式。

根據‘‘沒有免費的午餐’’ 定理，說明了沒有普遍優越的機器學習演算法。前饋網路提供了表示函式的萬能系統，在這種意義上，給定一個函式，存在一個前饋網路能夠近似該函式。但不存在萬能的過程既能夠驗證訓練集上的特殊樣本，又能夠選擇一個函式來擴充套件到訓練集上沒有的點。
總之，具有單層的前饋網路足以表示任何函式，但是網路層可能大得不可實現，並且可能無法正確地學習和泛化。在很多情況下，使用更深的模型能夠減少表示期望函式所需的單元的數量，並且可以減少泛化誤差。

這裡文章作者證明了網路擬合任意連續函式的萬能近似能力。直觀上，由於集合函式（set function）的連續性，一個輸入點集中的小擾動不太可能極大地改變函式的數值（如分類或分割score）。正式分析： 令 $\mathcal X=\{S:S \subseteq [0,1]^m \text{and}\vert S\vert=n\}$， $f:\mathcal X \to \mathbb R$是一個 $\mathcal X$上對Hausdroff距離 $d_H(\cdot,\cdot)$連續的集合函式，即 $\forall\epsilon\gt 0$， $\exists\delta\gt 0$使得對於任意 $S，S'\in \mathcal X$，若 $d_H(S,S')\lt\delta$