【微--策--略】

1. 五個洞排成一排，其中一個洞裡藏有一隻狐狸。每個夜晚，狐狸都會跳到一個相鄰的洞裡；每個白天，你都只允許檢查其中一個洞。怎樣才能保證狐狸最終會被抓住？

解答：有個問題 錯了 下面是少一天的推理 第一天2洞 第二天2洞 都沒有的話 證明它在後三個裡面 第三天4洞 第四天4洞 都沒有的話 證明第三天的時候 它在3號洞 第四天去了2號洞 第五天3洞 它如果不在 它肯定在1號洞 第六天在2號洞抓到它 bingo？

2.  5個海盜分100個金幣問題

首先從5號海盜開始，因為他是最安全的，沒有被扔下大海的風險，因此他的策略也最為簡單，即最好前面的人全都死光光，那麼他就可以獨得這100枚金幣了。 
接下來看4號，他的生存機會完全取決於前面還有人存活著，因為如果1號到3號的海盜全都餵了鯊魚，那麼在只剩4號與5號的情況下，不管4號提出怎樣的分配方案，5號一定都會投反對票來讓4號去喂鯊魚，以獨吞全部的金幣。哪怕4號為了保命而討好5號，提出（0，100）這樣的方案讓5號獨佔金幣，但是5號還有可能覺得留著4號有危險，而投票反對以讓其喂鯊魚。因此理性的4號是不應該冒這樣的風險，把存活的希望寄託在5號的隨機選擇上的，他惟有支援3號才能絕對保證自身的性命。 
再來看3號，他經過上述的
 
邏輯推理之後，就會提出（100，0，0）這樣的分配方案，因為他知道4號哪怕一無所獲，也還是會無條件的支援他而投贊成票的，那麼再加上自己的1票就可以使他穩獲這100金幣了。 
但是，2號也經過推理得知了3號的分配方案，那麼他就會提出（98，0，1，1）的方案。因為這個方案相對於3號的分配方案，4號和5號至少可以獲得1枚金幣，理性的4號和5號自然會覺得此方案對他們來說更有利而支援2號，不希望2號出局而由3號來進行分配。這樣，2號就可以屁顛屁顛的拿走98枚金幣了。 
不幸的是，1號海盜更不是省油的燈，經過一番推理之後也洞悉了2號的分配方案。他將採取的策略是放棄2號，而給3號1枚金幣，同時給4號或5號2枚金幣，即提出（97，0，1，2，0）或（97，0，1，0，2）的分配方案。由於1號的分配方案對於3號與4號或5號來說，相比2號的方案可以獲得更多的利益，那麼他們將會投票支援1號，再加上1號自身的1票，97枚金幣就可輕鬆落入1號的
 
腰包

3. Project Euler15 給定一個20*20的方格，從左上角到右下角的路徑有多少條？（只允許向右和向下走)

首先我們來討論一下2*2方格的情況：

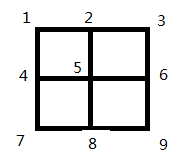
從結點1到結點9的走法：

1-2-3-6-9

1-2-5-6-9

1-2-5-8-9

1-4-7-8-9

1-4-5-6-9

1-4-5-8-9

共有6種不同的走法，仔細的讀者會發現，在結點3，6，7，8到結點9的通道只有一種，是的，這將會是以後解決問題的關鍵之一。

現在我們將方格數推廣到n，定義f（n,n）為結點（0，0）到結點（n，n）的通道數。

演算法如下：

方法一：遞推法

• 遞推公式為f(n,n)=f(n-1,n)+f(n,n-1)；
• 初始化條件:當0 <= i <= n,f(n,i)=1,f(i,n)=1。（初始條件的尋找，還得看讀者的觀察能力了）

方法二：排列組合

• f(n,n)=c(n,n+n)，其中c(n,n+n)表示n+n中取n

現在我只研究方法一，實現的程式碼如下：

#include <iostream>
#include <TIME.H>
using namespace std;
#define MAX_X 21
#define MAX_Y 21
/*遞迴*/
_int64 Recursion()
{
	_int64 a[MAX_X][MAX_Y] ;
	for(int i=0;i<=MAX_X-1;i++)
	{
		a[MAX_X-1][i]=1;
		a[i][MAX_Y-1]=1;
	}
	for (int j=MAX_X-2;j>=0;--j)
		for(int i1=MAX_Y-2;i1>=0;i1--)
			a[j][i1]=a[j+1][i1]+a[j][i1+1];

	return a[0][0];
}
int main()
{
	printf("%I64d",Recursion());
	return 0;
}

 

執行結果：137846528820

演算法，雖不是最好，但只為追求更好，還望不吝賜教！！！

*************************************

4.  在一光滑的平面上 左邊有m個小球以v的速度向右運動 右邊有n個小球以同樣的速度向左運動 球的質量相同 且發生完全彈性碰撞 問共碰撞多少次啊

提問者採納

m*n次（前提是質量相等,否則無解）
左一，右二，撞2次
左二，右二，撞4次
左二，右三，撞6次
。
。
。
左m，右n，撞m*n次

5.  在一光

某同學編了一個ax^2+bx+c=0的程式，任何輸入均有輸出，請設計測試用例！！

 

設：ax^2 =A；bx=B；c=C；
1.A=0,B=0,C=0; 
2.A+B=0,C=0;
3.A+C=0,B=0;
4.C+B=0,A=0;
這個思路看得懂吧？就是按這個思路去設計。

6

ddd

dddddddd

隨筆- 74  文章- 0  評論- 14 

【演算法題】rand5()產生rand7()

前兩天，睡覺前，偶爾翻起演算法導論，看到隨機函式這一塊內容，裡面有一個練習題．

5.1-2 描述random(a,b)過程的一種實現，它只調用random(0,1).作為a和b的函式，你的程式的期望執行時間是多少？

注：random(a,b)為產生a,a+1,a+2,...,b的函式發生器，且產生各整數的概率相等，同為1/(b - a + 1)．

看到這個題目時，似曾相識，腦海浮現了利用random(0,1)產生0或1，從而組成二進位制數，來完成random(a,b)的實現．但是細想以後，感覺有個問題在腦海中有點不明不白．

執行random(0,1)函式k次，使得2^k>=(b-a+1)，將得到[0,2^k)的整數區間，如何將[0,2^k)對映到[a,b]的整數區間，保證產生各整數的概率相等，同為1/(b-a+1).

1.當存在k使得2k=(b-a+1)時，只需將產生的二進位制數與[a,b]整數一一對應，即可滿足概率同為1/(b-a+1)的要求．

例如，random(3,6)，k=2.　此時，對應關係可為00~3,01~4,10~5,11~6．產生的概率為1/4.

2.當不存在k使得2k=(b-a+1)時，產生[0,2^k)區間整數的概率為1/2^k，小於1/(b-a+1)．[0,2^k)如何對映到[a,b]整數區間．

思路一：擴大[0,2^k)區間，使得2k可以被(b-a+1)整除，這樣可以把[0,2^k)分成N段時，每一段對應[a,b]裡的一個整數．

但這個思路，是不可行的，因為不存在這樣的k值．要麼2k=(b-a+1)，要麼2k>(b-a+1)且不可被(b-a+1)整除．

思路二：參取截斷對映，即 [0,2^k) 的前部分對映到[a,b]，這樣雖然可以達到產生整數的概率相等，但不等於1/(b-a+1)，還有如果產生[0,2^k)後部分的值如何處理．

這個思路，是可行的，如果產生後部分的值，就繼續呼叫自身，重新random.從結果輸出分析，最終random(a,b)最終輸出的只有[a,b]裡的整數，而且每個整數的概率相等，因而其產生的概率值是1/(b-a+1).

具體的實現程式碼如下：

 

 

int random(int a,int b)
{
    int m = 1;
    int len = b - a + 1;
    int k = 0;
    //計算最小的正整數k,使2^k >= len
    while(m < len)
    {
        k++;
        m *= 2;
    }
    m = 0;
    for(int i = 0;i < k;i++)
    {
        m += random(0,1) * (1<<i);
    }
    if(m + 1 > len)        
    {
        return random(a,b);
    }
    else
    {
        return m + a;
    }
}

 

dd

http://www.cnblogs.com/dwdxdy/archive/2012/07/28/2613135.html