之前一直太忙，沒時間整理，這兩天抽出點時間整理一下卷積、反捲積、池化、反池化的內容，也希望自己對一些比較模糊的地方可以理解的更加清晰。

一、卷積

1、卷積的簡單定義

卷積神經網路中的卷積操作可以看做是輸入和卷積核的內積運算。其運算過程非常容易理解，下面有舉例。

2、舉例解釋

（1）為了方便直接解釋，我們首先以一個通道（若是彩圖，則有RGB的顏色，所以是三個通道）為例進行講解，首先明確概念：

1） 輸入是一個5*5的圖片，其畫素值如下：
$[$

1 1 1

0 0 0

1 1 1 0 0 0 1 1 1 0 0 1 1 0 0 1 1 0 0 ] \begin{bmatrix} 1 & 1 &1 & 0 & 0\\ 0 & 1 & 1 &1 & 0\\ 0 & 0 & 1 & 1 & 1\\ 0 & 0 & 1 & 1 &0 \\ 0 &1 &1 & 0 &0 \end{bmatrix}
2）卷積核（kernel）是需要訓練的引數，這裡為了講解卷積運算的操作，所以最開始我們假設卷積核的值如下：
$\begin{bmatrix} 1 & 0 &1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \\ \end{bmatrix}$
3）通過視窗和卷積核的內積操作得到的結果叫做feature map。

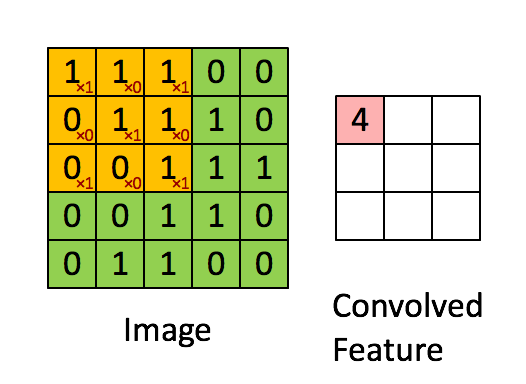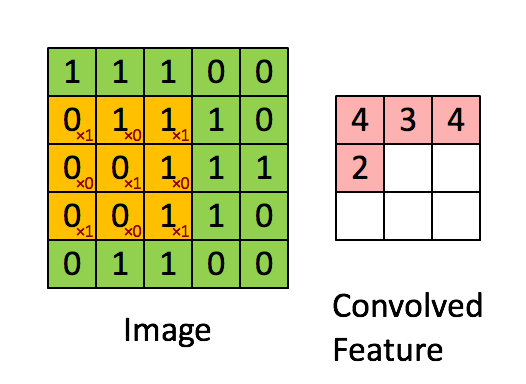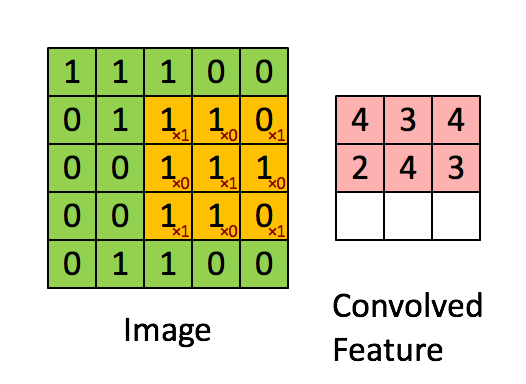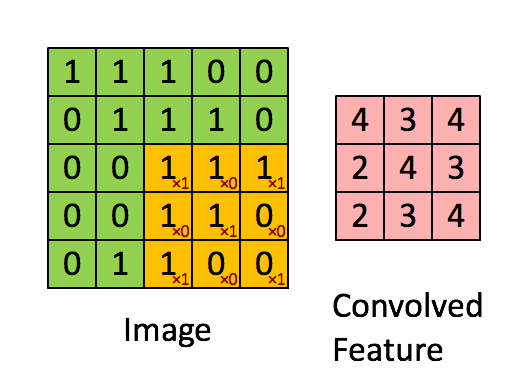
（2）如下圖所示（對應的是上面提到的資料），我們在輸入圖片上框出一個和卷積核相同大小的區域，基於此計運算元區域和卷積核對應元素乘積之和：
注： 本節圖形來自對FCN及反捲積的理解

$1*1 + 1*0+1*1+0*0+1*1+1*0+0*1+0*0+1*1=4$
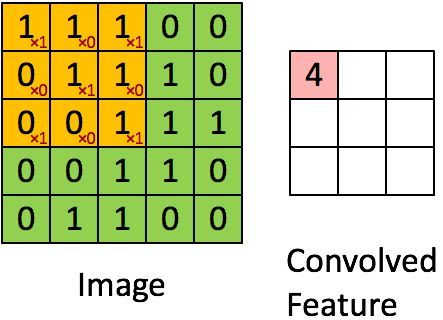
所以feature map的第一個元素值為4。

（3）接著計算第二個子區域和卷積核的對應元素乘積之和，如下圖所示：

$1*1+1*0+0*1+1*0+1*1+1*0+0*1+1*0+1*1=3$
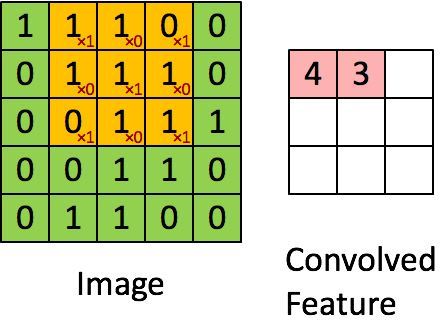
所以feature map的第二個元素值為3。

（4）接著計算第三個子區域和卷積核的對應元素乘積之和，如下圖所示：

$1*1+0*0+0*1+1*0+1*1+0*0+1*1+1*0+1*1=4$
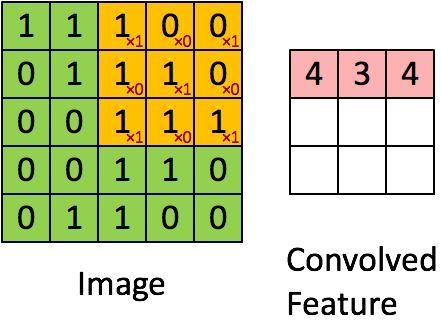
所以feature map的第三個元素值為4。

（5）接著計算第四個子區域和卷積核的對應元素乘積之和，如下圖所示：

$0*1+1*0+1*1+0*0+0*1+1*0+0*1+0*0+1*1=2$
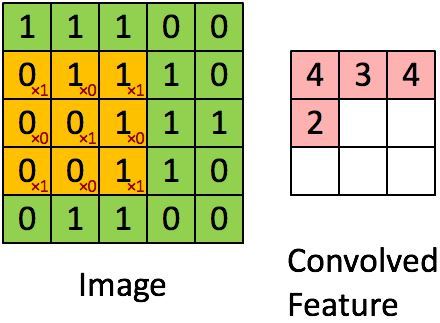
所以feature map的第四個元素值為2。

（6）以此類推，不斷執行，最後得到的feature map如下：

$\begin{bmatrix} 4 & 3&4 \\ 2 & 4 & 3 \\ 2& 3 & 4 \\ \end{bmatrix}$
（7）下面的動圖可以連貫的展示上面的過程，可以幫助更直觀的理解：

3、多個輸入通道

若輸入含有多個通道，則對於某個卷積核，分別對每個通道求feature map後將對應位置相加得到最終的feature map，如下圖所示：

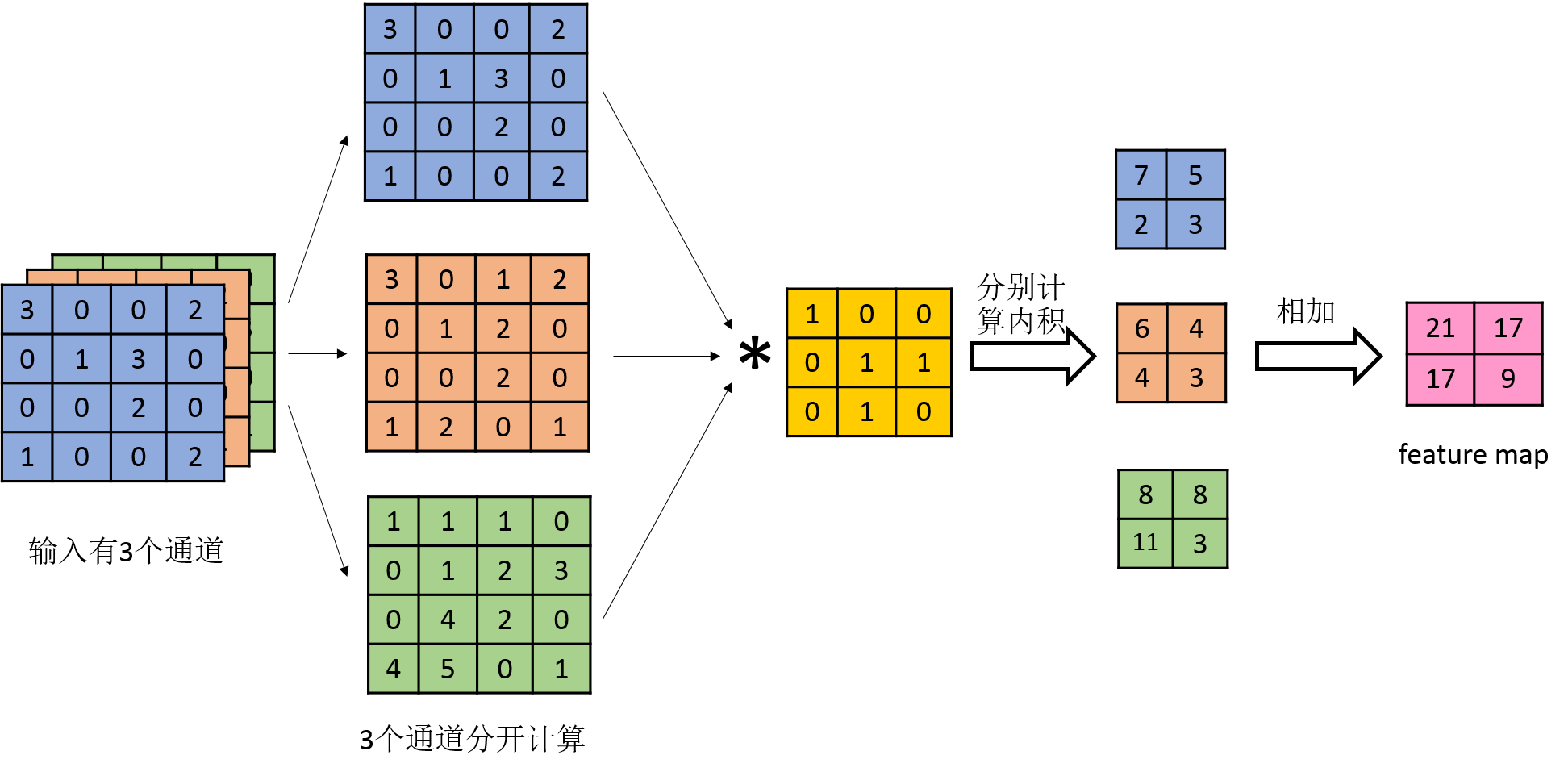
4、多個卷積核

若有多個卷積核，則對應多個feature map，也就是下一個輸入層有多個通道。如下圖所示：

5、步數的大小

上述展示的步長為1的情況，若步長為2，則滑動視窗每2步產生一個，如下圖所示：

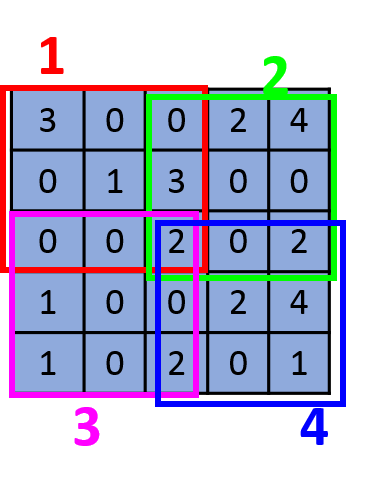
輸入大小為55，卷積核的大小為33，第一個滑動視窗為紅色部分，第二個滑動視窗為綠色部分，第三個滑動視窗為紫色部分，第四個滑動視窗為藍色部分，所以最後的feature map的大小為2*2。

若假設輸入大小是 $n*n$，卷積核的大小是 $f*f$，步長是 $s$，則最後的feature map的大小為 $o*o$，其中 $o$如下：
$o=\left \lfloor \frac{n-f}{s} \right \rfloor+1$