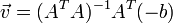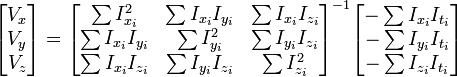Lucas–Kanade光流演算法學習
Lucas–Kanade光流演算法是一種兩幀差分的光流估計演算法。它由Bruce D. Lucas 和 Takeo Kanade提出。
H.O.T. 指更高階,在移動足夠小的情況下可以忽略。從這個方程中我們可以得到: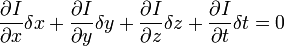
或者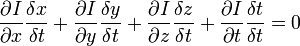
我們得到: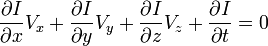
V x ,V y ,V z 分別是I(x,y,z,t)的光流向量中x,y,z的組成。 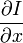 ,
, 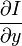 ,
, 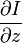 和
和 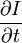 則是影象在(x
則是影象在(x
所以
I x V x + I y V y + I z V z = − I t。
這個方程有三個未知量,尚不能被解決,這也就是所謂光流演算法的光圈問題。那麼要找到光流向量則需要另一套解決的方案。而Lucas-Kanade演算法是一個非迭代的演算法:
假設流(Vx,Vy,Vz)在一個大小為m*m*m(m>1)的小窗中是一個常數,那麼從畫素1...n , n = m 3 中可以得到下列一組方程:(也就是說,對於這多個點,它們三個方向的速度是一樣的)即,假設了在一個畫素的周圍的一個小的視窗內的所有畫素點的光流大小是相同的。
(
而兩幀影象之間的變化,就是t方向的梯度值,可以理解為當前畫素點沿著光流方向運動而得到的,所以我們可以得到上邊的這個式子。令:
)
三個未知數但是有多於三個的方程,這個方程組自然是個超定方程,也就是說方程組內有冗餘,方程組可以表示為:
這也就是說尋找光流可以通過在四維上影象導數的分別累加得出。我們還需要一個權重函式W(i, j,k) ,  來突出視窗中心點的座標。高斯函式做這項工作是非常合適的,
來突出視窗中心點的座標。高斯函式做這項工作是非常合適的,
這個演算法的不足在於它不能產生一個密度很高的流向量,例如在運動的邊緣和黑大的同質區域中的微小移動方面流資訊會很快的褪去。它的優點在於有噪聲存在的魯棒性還是可以的。
補充:opencv裡實現的看上去蠻複雜,現在還不是太明白。其中LK經典演算法也是迭代法,是由高斯迭代法解線性方程組進行迭代的。
參考資料:http://www.cnblogs.com/gnuhpc/archive/2012/12/04/2802124.html
這一部分《learing opencv》一書的第10章Lucas-Kanade光流部分寫得非常詳細,推薦大家看書。
另外我對這一部分附上一些個人的看法(謬誤之處還望不吝指正):
1.首先是假設條件:
(1)亮度恆定,就是同一點隨著時間的變化,其亮度不會發生改變。這是基本光流法的假定(所有光流法變種都必須滿足),用於得到光流法基本方程;
(2)小運動,這個也必須滿足,就是時間的變化不會引起位置的劇烈變化,這樣灰度才能對位置求偏導(換句話說,小運動情況下我們才能用前後幀之間單位位置變化引起的灰度變化去近似灰度對位置的偏導數),這也是光流法不可或缺的假定;
(3)空間一致,一個場景上鄰近的點投影到影象上也是鄰近點,且鄰近點速度一致。這是Lucas-Kanade光流法特有的假定,因為光流法基本方程約束只有一個,而要求x,y方向的速度,有兩個未知變數。我們假定特徵點鄰域內做相似運動,就可以連立n多個方程求取x,y方向的速度(n為特徵點鄰域總點數,包括該特徵點)。
2.方程求解
多個方程求兩個未知變數,又是線性方程,很容易就想到用最小二乘法,事實上opencv也是這麼做的。其中,最小誤差平方和為最優化指標。
3.好吧,前面說到了小運動這個假定,聰明的你肯定很不爽了,目標速度很快那這貨不是二掉了。幸運的是多尺度能解決這個問題。首先,對每一幀建立一個高斯金字塔,最大尺度圖片在最頂層,原始圖片在底層。然後,從頂層開始估計下一幀所在位置,作為下一層的初始位置,沿著金字塔向下搜尋,重複估計動作,直到到達金字塔的底層。聰明的你肯定發現了:這樣搜尋不僅可以解決大運動目標跟蹤,也可以一定程度上解決孔徑問題(相同大小的視窗能覆蓋大尺度圖片上儘量多的角點,而這些角點無法在原始圖片上被覆蓋)。








三.opencv中的光流法函式
opencv2.3.1中已經實現了基於光流法的特徵點位置估計函式(當前幀位置已知,前後幀灰度已知),介紹如下(摘自opencv2.3.1參考手冊):
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
四.用類封裝基於光流法的目標跟蹤方法
廢話少說,附上程式碼,包括特徵點提取,跟蹤特徵點,標記特徵點等。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
|
轉載自:http://www.xuebuyuan.com/2023445.html
matlab 參考程式 如下:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 |
|

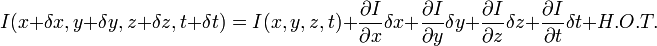
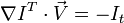


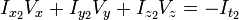

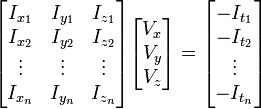
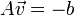
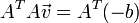 or
or