Newton's Method

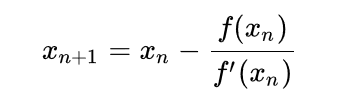
Integer Square Root

難點在於計算x0，第一種方法x0 = 2^k >= sqrt(n)，k取最小值

/// <summary>
/// 返回<paramref name="n"/>平方根,向下取整
/// </summary>
public static int IntegerSquareRoot(uint n)
{
    if (n <= 1) return (int)n;

    var s = 1;
    var t = n - 1;
    if (t > 0xFFFFu) { s += 8; t >>= 16; }
    if (t > 0xFFu) { s += 4; t >>= 8; }
    if (t > 0xFu) { s += 2; t >>= 4; }
    if (t > 0x3u) { s += 1; }

    var g0 = 1u << s; // g0 = 2^s
    while (true)
    {
        var g1 = (g0 + (n / g0)) >> 1;// g1 = (g0 + n/g0)/2

        if (g0 <= g1)
            break;

        g0 = g1;
    }

    return (int)g0;
}
 

第二種方法通過（n - 1）前導0的個數來計算

/// <summary>
/// 返回<paramref name="n"/>平方根,向下取整
/// </summary>
public static int IntegerSquareRoot2(uint n)
{
    if (n <= 1) return (int)n;

    var s = 16 - ((n - 1).NumberOfLeadingZeros() >> 1);

    var g0 = 1u << s; // g0 = 2^s
    while (true)
    {
        var g1 = (g0 + (n / g0)) >> 1;// g1 = (g0 + n/g0)/2

        if (g0 <= g1)
            break;

        g0 = g1;
    }

    return (int)g0;
}



/// <summary>
/// <paramref name="n"/>二進位制前導0的個數
/// </summary>
public static int NumberOfLeadingZeros(this uint n)
{
    if (n == 0u) return 32;

    var c = 1;
    if ((n >> 16) == 0u) { c += 16; n <<= 16; }
    if ((n >> 24) == 0u) { c +=  8; n <<=  8; }
    if ((n >> 28) == 0u) { c +=  4; n <<=  4; }
    if ((n >> 30) == 0u) { c +=  2; n <<=  2; }

    return c - (int)(n >> 31);
}
 

二進位制版本

/// <summary>
/// 返回<paramref name="n"/>平方根,向下取整
/// </summary>
public static int IntegerSquareRootBinary(uint n)
{
    var m = 0x40000000u;
    var y = 0u;
    while (m != 0u)
    { // Do 16 times.
        var t = y | m;
        y >>= 1;
        if (n >= t)
        {
            n -= t;
            y |= m;
        }
        m >>= 2;
    }

    return (int)y;
}
 

Integer Cube Root

x0不好準確估值，從而減少計算量，無法給出牛頓方法版本，只有二進位制版本

/// <summary>
/// <paramref name="n"/>立方根,向下取整
/// </summary>
public static int IntegerCubeRoot(uint n)
{
    var t = 0u;
    for (var s = 30; s >= 0; s = s - 3)
    {
        t <<= 1;
        var b = (3 * t * (t + 1) + 1) << s;
        if (n >= b)
        {
            n -= b;
            t += 1;
        }
    }

    return (int)t;
}

Reverse Bits

/// <summary>
/// <paramref name="n"/>二進位制反向後的整數
/// </summary>
public static uint ReverseBits(uint n)
{
    n = (n & 0x55555555u) << 1 | (n >> 1) & 0x55555555u;
    n = (n & 0x33333333u) << 2 | (n >> 2) & 0x33333333u;
    n = (n & 0x0F0F0F0Fu) << 4 | (n >> 4) & 0x0F0F0F0Fu;
    n = (n << 24) |
        ((n & 0xFF00u) << 8) |
        ((n >> 8) & 0xFF00u) |
        (n >> 24);

    return n;
}



/// <summary>
/// <paramref name="n"/>二進位制反向後的整數
/// </summary>
public static ulong ReverseBits(ulong n)
{
    n = (n << 32) | (n >> 32); // Swap register halves.
    n = (n & 0x0001_FFFF_0001_FFFFUL) << 15 | // Rotate left
        (n & 0xFFFE_0000_FFFE_0000UL) >> 17; // 15.

    var t = (n ^ (n >> 10)) & 0x003F_801F_003F_801FUL;
    n = (t | (t << 10)) ^ n;
    t = (n ^ (n >> 4)) & 0x0E03_8421_0E03_8421UL;
    n = (t | (t << 4)) ^ n;
    t = (n ^ (n >> 2)) & 0x2248_8842_2248_8842UL;
    n = (t | (t << 2)) ^ n;

    return n;
}