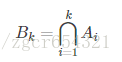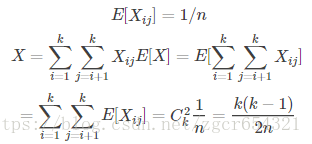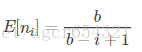演算法導論 第五章:概率分析和隨機演算法 筆記(僱傭問題、指示器隨機變數、隨機演算法、概率分析和指示器隨機變數的進一步使用)
僱傭問題:
假設你需要僱用一名新的辦公室助理。你先前的僱傭嘗試都以失敗告終,所以你決定找一個僱用代理。僱用代理每天給你推薦一個應聘者。你會面試這個人,然後決定要不要僱用他。你必須付給僱用代理一小筆費用來面試應聘者。要真正地僱用一個應聘者則要花更多的錢,因為你必須辭掉目前的辦公室助理,還要付一大筆中介費給僱用代理。你的諾言是在任何時候,都要
找到最佳人選來擔任這項職務。因此,你決定在面試完每個應聘者後,如果這個應聘者比目前的辦公助理更有資格,你就會辭掉目前的辦公室助理,然後聘請這個新的應聘者。你願意為這種策略而付出費用,但希望能夠預測這種費用會是多少。
下面給出的HIRE-ASSISTANT過程以偽程式碼表達這種僱用策略。它假設應聘辦公室助理工作的人編號為1到n。此過程假設你能夠在面試完應聘者i後,決定應聘者i是否是你見過的最適當人選。為了初始化,此程式建立一個虛擬的應聘者,編號為0, 他的應聘條件比所有其他的應聘者都差。
HIRE-ASSISTANT(n)
best ← 0 candidate 0 is a least-qualified dummy candidate
for i ← 1 to n
do interview candidate i
if candidate i is better than candidate best
then best ← i
hire candidate i假設面試費用為Ci,僱傭的費用為Ch,假設整個過程中僱傭了m次,於是總的費用是 nCi+mCh。由於n是固定值(注意n個人總是要全部面試完的,所以面試的費用是一定的),總費用的變化取決於m值。
最壞情況:
最壞情況下,我們僱傭了每一個應聘者,m=n。
概率分析:
事實上,我們既不能得知應聘者出現的順序,也不能控制這個順序,因此我們使用概率分析。概率分析就是在問題的分析中使用概率技術。為了使用概率分析,必須使用關於輸入分佈的知識或者對其做假設,然後分析演算法,計算出一個期望的執行時間。
有些問題,我們對所有可能的輸入集合做某種假設。對於其他問題,可能無法描述一個合理的輸入分佈,此時就不能使用概率分析方法。
在僱傭問題中,可以假設應聘者是以隨機順序出現的。假設可以對任何兩個應聘者進行比較並確定哪個更優;換言之,在所有的應聘者之間存在這一個全序關係。因此可以使用從1到n的唯一號碼來標誌應聘者的優秀程度。用rank(i)來表示應聘者i的名次。
隨機演算法:
在許多情況下,我們對輸入分佈知識知之甚少;即使知道關於輸入分佈的某些資訊,也無法對這種分佈建立模型。然而通過使一個演算法中的某些部分的行為隨機化,就常常可以利用概率和隨機性作為演算法設計和分析的工具。
比如在僱傭問題中,如果僱傭代理給我們一份應聘者的名單,每天我們隨機地挑選一個應聘者進行面試,從而確保了應聘序列的隨機性。
更一般地,如果一個演算法的行為不只有輸入決定,同時也由隨機數生成器所產生的數值決定,則稱這個演算法是隨機的。我們將假定有一個可以自由使用的隨機數生成器RANOOM。呼叫RANDOM(a, b) 將返回一個介於a 與b 之間的整數,而每個整數出現的機會相等。
如:
概率分析和隨機演算法的區別:
概率分析是對輸入做假設,假設輸入服從某種分佈(例如假設輸入是隨機的),然後根據假設的概率前提來分析期望情況。而隨機演算法是通過一個演算法來重新排列輸入,使得輸入變的隨機化。
指示器隨機變數:
給定一個樣本空間S和一個事件A,那麼事件A對應的指示器變數I{A}定義為:
I{A}=1 如果A發生
I{A}=0 如果A不發生
一個事件A對應的指示器變數的期望值等於事件A發生的概率。
根據反映期望線性性質的等式,容易計算出總和的期望值:它等於n個隨機變數的期望值。期望的線性性質利用指示器隨機變數作為一種強大的分析技術。當隨機變數之間存在關係時也成立。
如:
事件A對應的指示器隨機變數的期望值等於事件A發生的概率。
引理5.1 給定樣本空間S和S中的事件A, 令XA = I{A}, 則E[XA]=Pr{A} 。
下面我們用兩種方法來求僱用問題的期望:
概率分析的方法:
假設應聘者以隨機的順序出現,令X作為一個隨機變數,其值等於僱傭新的辦公室經理的次數。那麼 E[X] = ∑xPr{X=x},但這一計算會很麻煩。
其形式類似於這樣:
欲求X的期望,X可取的值有1,2,3,,,,,n。然後分別列出取每個值時的概率
X 1 2 3,,,,n
P p1 p2 p3,,,pn
E[X] = ∑xPr{X=x}來求期望。注意這裡每一個p值都要用排列組合裡面的知識來求,對於這個題目來說還不是很難,但有的題目比這個難多了,另外還要對每一項x和p的乘積相加,求和過程往往是一個變形技巧很高的過程。
用指示器隨機變數的方法來求期望:
我們定義n個和每個應聘者是否被僱傭對應的變數,Xi為對應於第i個應聘者被僱傭這個事件的指示器隨機變數。
有X=X1+X2+...+Xn。(X仍然是概率分析方法中的隨機變數X,這裡我們換一種方式來求X,相當於把X分解了)
E[Xi] = Pr{Xi} = 1/i,因為應聘者是隨機出現的,所以第i個應聘者比前面i-1個優秀的概率是1/i。
因此E[X] = 1+1/2+1/3+...+1/n。
E[X] = 1+1/2+1/3+...+1/n
=ln(n) + O(1)
即:面試了n個人,實際上大約只僱傭了ln(n)次。假設應聘者以隨機順序出現,演算法HIRE-ASSISTANT 總得僱傭費用為O(ch*lnn)。
概率分析和指示器隨機變數的區別在哪?
概率分析對所求隨機變數X是分情況把X能取到的每個值的概率都求出來,然後像高中求期望那樣,相乘相加。
指示器隨機變數將所求的隨機變數X分解成了許多單個的事件,對於每一個事件一一的求期望,加起來即可。
隨機演算法:
很多隨機演算法通過使輸入隨機化來實現,書中介紹了兩種隨機陣列的構造方法:
1、隨機排列陣列
為陣列A[i]賦一個隨機的優先順序P[i],然後依據P[i]對A[i]進行排序,即可得到隨機陣列;
如:
初始陣列A =(1 , 2, 3 , 4 ) 且選擇隨機的優先順序P =( 36 ,3, 97, 19),將得出數列B = (2, 4, 1, 3),因為第2個優先順序最小,接著是第4個,然後第1個,最後是第3個。
稱這個過程為PERMUTE-BY-SORTING:
第3行選取一個在1到n3之間的隨機數。使用範圍1到n3,是為了讓P中的所有優先順序儘可能是唯一的。
2、原址排列給定陣列
產生隨機排列的一個更好方法是原地排列給定的數列。程式RANDOMIZE-IN-PLACE在O(n) 時間內完成。在第t次迭代時,元素A[i]是從元素A[i]到A[n] 中隨機選取的。第t次迭代之後,A[i]保持不變。
概率分析和指示器隨機變數的進一步使用:
生日悖論:
問題:一個屋子裡人數必須要達到多少人,才能使其中兩人生日相同的機會達到50%?
概率分析:
至少有兩個人生日相同的概率 = 1 - 所有人生日都不相同的概率。
其中Ai是指所有j<i,i與j生日不同的事件,則有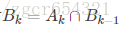
其中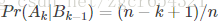
n=365時,k>=23。
指示器隨機變數:
定義指示器隨機變數Xij,有
當k(k−1)≥2n時,生日相同的兩人對的期望數至少是1。
球與箱子(禮券收集者問題):
問題:b個箱子,在平均意義下必須要投多少個球,才能每個箱子至少都投進一球(球落在每個箱子等可能的)。 第i階段包括從第i-1次命中到第i次命中之間的投球。設ni表示第i階段的投球次數,所以b次命中所需的投球此引數為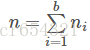
所以有
特徵序列:
問題:假設拋投一枚標準的硬幣n次,最長連續正面的序列的期望長度有多長?答案是Θ(lgn)
如,對n=1000次硬幣拋擲,出現一系列最少為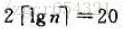
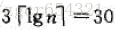
線上僱傭問題:
問題:公司應聘員工,當有更好的申請者出現則僱傭新人解僱舊人,如何在最小化面試次數、僱傭成本和最大化僱傭應聘者的質量取得平衡。
策略:選擇一個正整數k<n,面試然後拒絕前k個應聘者,再僱傭其後比前面最高分數還高的第一個應聘者。 如果結果是最好的應聘者在前k個面試的之中,那麼我們將僱用第n個應聘者。這個策略形式化地表示在如下所示的過程ON-LINEMAXIMUM(k,n)中。