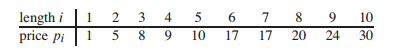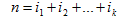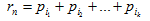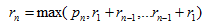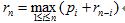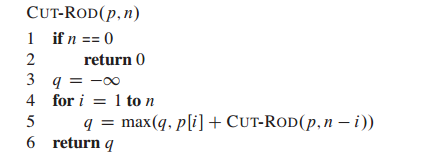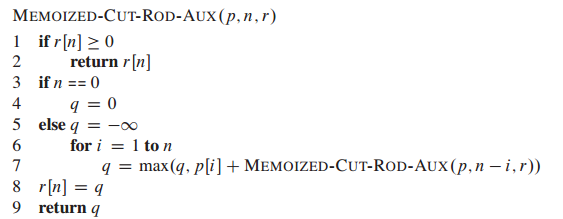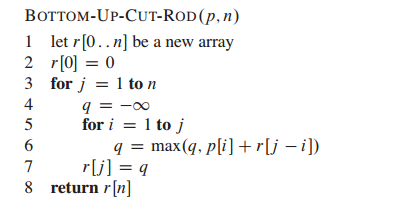演算法導論 第十五章:動態規劃之棒的切割(Rod Cutting)
阿新 • • 發佈:2018-12-27
和分治法一樣,動態規劃(Dynamic programming)是通過組合子問題的解而解決整個問題的。
其不同點在於:
1)分治法是將問題劃分成一些獨立的子問題,遞迴求解各個子問題,然後合併子問題的解而得到原問題的解
2)動態規劃使用於子問題不獨立的情況,也就是各個子問題包含公共的部分。若採用分治法,會有重複的求解公共部分,而動態規劃演算法對每個子問題只求解一次,然後搶劫過儲存在一張表中,從而避免重複的運算。
動態規劃具有如下特徵:
1)最優子結構
2)重疊子問題
動態規劃演算法設計可以分為如下步驟:
1)描述最優解的結構
2)遞迴定義最優解的值
3)按自底向上的方式計算最優解的值
3)由計算出的結果構造一個最優解
棒切割(Rod Cutting)問題:
一段長為n的棒,若長為i,其價格為Price(i) 其中i=1,2,...,n (價格表如下), 如何切割可以使得收益r(n)最大?
若最優解將棒分成k段,1 ≤ k ≤ n,則可以分解為:
收益為表示為:
更一般地,我們可以從更短切割的收益中重構最優收益:
簡化上式可得:
最優解決方法:
1)遞迴(Recursive)
虛擬碼如下:
執行時間為:T(n)=2^n
2)帶備忘錄的自頂向下方法(Top-down with memoization)
虛擬碼如下:
3)自底向上方法(Bottom-up method)
上面三種方法可以求得最大收益,但是不能給出具體切割方法,為此我們需要重構最優解,虛擬碼如下:
完整程式碼如下:
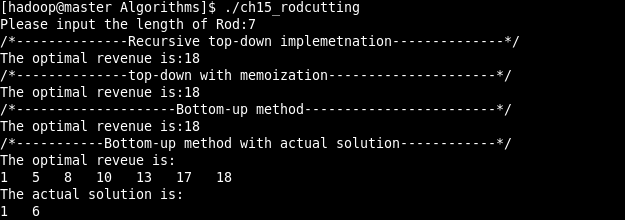
執行結果:#include<iostream> #include<cstdlib> #include<climits> using namespace std; int Recursive_CutRod(int *p,int n) { if(n==0) return 0; int r=INT_MIN; for(int i=1;i<=n;i++) r=max(r,p[i]+Recursive_CutRod(p,n-i)); return r; } int Memoized_CutRod_Aux(int *p,int n,int *r) { int q; if(r[n]>=0) return r[n]; if(n==0) q=0; else { q=INT_MIN; for(int i=1;i<=n;i++) q=max(q,p[i]+Memoized_CutRod_Aux(p,n-i,r)); } r[n]=q; return q; } int Memoized_CutRod(int *p,int n) { int *r=new int[n+1]; for(int i=0;i<=n;i++) r[i]=INT_MIN; return Memoized_CutRod_Aux(p,n,r); } int *BottomUp_CutRod(int *p,int n) { int q; int *r=new int[n+1]; r[0]=0; for(int j=1;j<=n;j++) { q=INT_MIN; for(int i=1;i<=j;i++) q=max(q,p[i]+r[j-i]); r[j]=q; } return r; } void Ex_BottomUp_CutRod(int *p,int n,int *r,int *s) { r[0]=0; for(int j=1;j<=n;j++) { int q=INT_MIN; for(int i=1;i<=j;i++) if(q<p[i]+r[j-i]){ q=p[i]+r[j-i]; s[j]=i; } r[j]=q; } } void Print_OpValue(int *r,int n) { for(int i=1;i<=n;i++) cout<<r[i]<<" "; cout<<endl; } void Print_Solution(int *s,int n) { while(n>0) { cout<<s[n]<<" "; n=n-s[n]; } cout<<endl; } int main() { int price[]={1,5,8,9,10,17,17,20,24,30}; //int n=sizeof(price)/sizeof(int); int n; cout<<"Please input the length of Rod:"; cin>>n; int *p=new int[n+1]; p[0]=n; for(int i=0;i<n;i++) p[i+1]=price[i]; cout<<"/*--------------Recursive top-down implemetnation--------------*/"<<endl; int res1=Recursive_CutRod(p,n); cout<<"The optimal revenue is:"<<res1<<endl; cout<<"/*--------------top-down with memoization---------------------*/"<<endl; int res2=Memoized_CutRod(p,n); cout<<"The optimal revenue is:"<<res2<<endl; cout<<"/*--------------------Bottom-up method------------------------*/"<<endl; int *res3=new int[n+1]; res3=BottomUp_CutRod(p,n); cout<<"The optimal revenue is:"<<res3[n]<<endl; cout<<"/*-----------Bottom-up method with actual solution------------*/"<<endl; int *res4=new int[n+1]; int *s=new int[n+1]; Ex_BottomUp_CutRod(p,n,res4,s); cout<<"The optimal reveue is:"<<endl; Print_OpValue(res4,n); cout<<"The actual solution is:"<<endl; Print_Solution(s,n); delete []p; return 0; }
【注:若有錯誤,請指正~~~】