【資料庫複習】函式依賴
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow
也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
如果我們要設計關係型資料庫的表模式,則很有可能會出現冗餘,為了避免這種情況,我們需要一些規則,這些規則稱為依賴。
函式依賴簡單地說就是屬性集A推匯出屬性集B,比如
![]()
給定這些規則之後,如果某個關係能夠滿足給定的函式依賴,則稱關係R滿足函式依賴F;
在下面我們會介紹一系列的正規化以及分解演算法;
函式依賴的分解合併規則
![]()
與
![]()
是等價的(可以互相轉化的),第一個式子替換第二個式子稱為合併規則,第二個式子替換第一個式子稱為分解規則;
平凡函式依賴:如果A-->B,A是B的超集,則稱此函式依賴為平凡的。
平凡依賴規則:如果A-->B,則可以將其變為A-->(B-A∩B),這樣可以消除冗餘;
鍵的函式依賴定義:
(1)如果存在某個屬性集,能夠蘊含全部的屬性;
(2)這個屬性集的任意真子集都不能蘊含全部屬性;
則稱這個屬性集為鍵;
函式依賴習題
平凡依賴規則
舉例:name,age --->name,course, 根據平凡依賴規則,可以簡化為 name,age -->course.
異常
如果一個關係的模式沒有設計好,則會出現異常。異常的型別為:
(1)冗餘:一個屬性的值多次出現,比如:
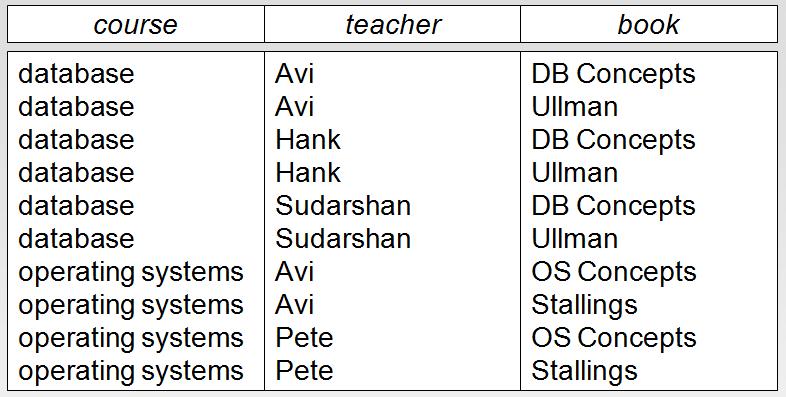
(2)更新異常:上圖的關係就存在更新異常,因為如果需要更新database這門課為database concept,則需要將左邊的database全部更新為database concept;
(3)刪除異常:上圖的關係存在刪除異常,因為將Avi、Hank、Sudarshan老師刪除,則會出現database這門課消失了,但實際上資料庫這門課永遠不會消失,而只是老師辭職了。
屬性閉包演算法

舉例:

閉包的應用
1.給定函式依賴集F1,是否可以推斷出函式依賴f:A-->B?
只需要求出{A}+是否包含B,如果包含,則說明F1能夠推斷出f,否則不能;
舉例:

2.判斷某個屬性集是否為鍵?
如果要證明屬性集是超鍵,則只需要計算此屬性集的閉包,看閉包中是否包含全部的屬性;
但是如果需要證明屬性集是候選鍵,則第一步需要證明是超鍵,第二步需要證明從屬性集中任意去掉一個屬性,此屬性集就不是超鍵;
3.給出一些術語.
給定一個函式依賴集A;
A的基本集:和A等價的函式依賴集;
A的最小化基本集:滿足(1)函式依賴的右邊只有單個屬性(2)刪除任意一個函式依賴都不將是基本集(3)從函式依賴的左邊刪除任意一個屬性,則不將是基本集;

4.投影函式依賴
給定一個關係和滿足的函式依賴F,求對部分屬性投影后,哪些函式依賴滿足。
比如:原本屬性為A,B,C的關係,投影到A,B後,還有哪些函式依賴成立?
簡單地說就是:
(1)首先計算單屬性的閉包,比如{A}的閉包為{B,C},如果我們的投影為{A,B},則需要包含A-->B,而不包含A-->C;(如果存在某個屬性集能夠蘊含所有屬性,則我們就不需要再求此屬性集的閉包)
(2)接著計算雙屬性,三屬性,四屬性.....;
(3)在求出的基本集中最小化;
--如果投影后的某個函式依賴能夠通過投影后的其他函式依賴推出,則刪除;
比如:{A-->C,A-->B,B-->C},刪除A-->C,因為此函式依賴能夠通過其他函式依賴推導;
--如果某個函式依賴A-->B,刪除A中某個屬性後仍然在投影的函式依賴中成立,則刪除;
比如:投影后的函式依賴為{AC-->B,A-->B},則把{AC-->B}刪除,因為如果刪除C即A-->B 能夠從投影的函式依賴中推出;
舉例:

5.判斷無損分解
如果R1∩R2是R1或R2的超碼,則R上的分解(R1,R2)是無損分解。
Armstrong公理

下面我們會說到BCNF分解和3NF分解,而分解也是有評判標準的:
(1)消除異常;
(2)無損連線:分解後再連線是否和原來的關係一致;
用chase檢驗法則;
(3)保持依賴:FD的投影在分解後的關係上成立,但是連線後的關係不滿足原始FD;
BCNF滿足(1)和(2),3NF滿足(1)(2)(3)
Chase檢驗法則
判斷分解後再自然連線是否還是原始的關係;
思想:自然連線後的每個元組都屬於原始關係;
如果將關係投影到Si後再進行自然連線,就會得到一個所有分量都不帶下標的元組,這個元組不在R中,則連線為無損的;
舉例:

保持依賴
思想:FD投影在分解的關係中成立,但是自然連線後不能滿足原始的FD
舉例:

BCNF
當關系滿足如果R中非平凡的函式依賴的左邊都是超鍵,則此關係R屬於BCNF;
性質:任何一個二元關係都滿足BCNF
證明:如果函式依賴集中存在A-->B,則我們可以說A-->AB,因此A一定是超鍵;
BCNF分解
注:BCNF分解是無損分解
while(找到違反BCNF的函式依賴){
找出違反BCNF的函式依賴A-->B,先計算A的閉包,且用A的閉包(除去A)替換B,並將其分解為{A+}和{AU(R-(A+)}; //比如A-->B ,而{A}+={A,B,C},則用A-->BC替換A-->B;
求出分解後的關係滿足的投影FD集合;
再看分解後的關係的FD集合是否滿足BCNF,如果不滿足,則繼續分解。
}
舉例:

3NF
注:3NF是能夠無損連線且保持依賴;
放鬆了BCNF的要求,多出的一個條件為:如果A-->B,則B-A為候選鍵的一部分(即使在不同的候選鍵中),則滿足3NF;
這裡我們對上句中的紅色標註部分進行解釋,看一個例子:
比如:存在函式依賴A-->BC,{AB}{AC}分別為候選鍵,而BC-A={BC},B屬於候選鍵{AB},C屬於候選鍵{AC},但是A-->BC仍然滿足3NF;
主屬性:一個屬性屬於某個候選鍵;
比如:{AC}為候選鍵,則A為主屬性,C也為主屬性;
3NF分解演算法

舉例:
1NF
每個屬性都保持原子性;
2NF
滿足1NF,且每一個非主屬性都完全函式依賴於R的主碼;
多值依賴
引入多值依賴的原因

從上圖中可以知道,此關係的候選鍵為(name,street,city,title,year),因此不存在任何非平凡的函式依賴,因此遵守BCNF,但是我們可以很容易看出,(street、city)和(title、year)是獨立的;放在一個關係中是冗餘的;
因此多值依賴的產生就是源於此;我們可以將上圖的關係根據4NF分解演算法分解關係;
多值依賴(MVD)定義
A1A2....An-->-->B1B2....Bm,則說明
(1)給定A1A2...An的值,B1B2...Bm屬性獨立於(U-A-B)屬性;
(2)給定R中的兩個元組a、b,他們的A屬性相同,則必然存在第三個元組c,使得c[A]=a[A]=b[A],c[B]=a[B],c[U-A-B]=b[U-A-B];
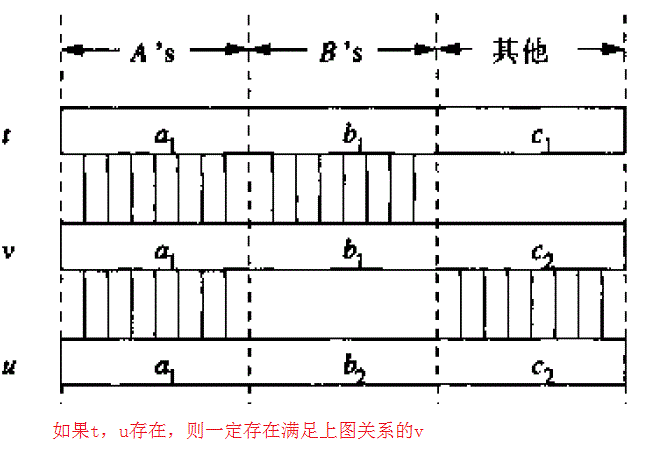
多值依賴性質
(0)多值依賴其實就是FD的升級,即如果A-->B成立,則A-->-->B也成立;
(1)平凡MVD:如果B是A的子集,則A-->-->B成立;
(2)附加平凡MVD:如果關係R(A,B),則A-->-->B成立;
(3)傳遞MVD:如果A-->-->B,B-->-->C,則A-->-->C成立;
(4)MVD不滿足分解規則:
(5)如果A-->-->B,則A-->-->(R-A-B)成立;

4NF
應用於MVD,而不是一般的FD;條件和BCNF差不多;
定義:如果存在非平凡的A-->-->B,且A一定是超鍵,則為4NF;
4NF分解演算法
1.找違反4NF的MVD;
2.按照A-->-->B 分解為{AB} {R-A-B};
3.計算投影FD;
4.繼續找違反的MVD,分解.....;

總結:
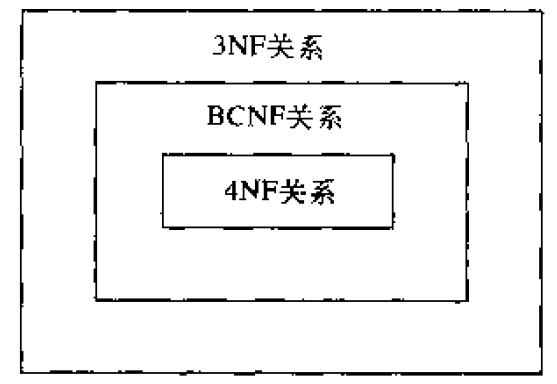
給我老師的人工智慧教程打call!http://blog.csdn.net/jiangjunshow

