給定一個二維陣列，每格為0/1值，1代表無法通過。求從左上到右下的不同路徑數。只能往右/下走。

Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

該題較62題多了個障礙的概念。方法相似，只要將障礙處的dp設為0即可（帶障礙說明其後續的路徑必然不會經過這裡），依然可知dp式子：dp [i] [j] = dp [i-1] [j] + dp [i] [j-1]，但是需要考慮幾種情況：

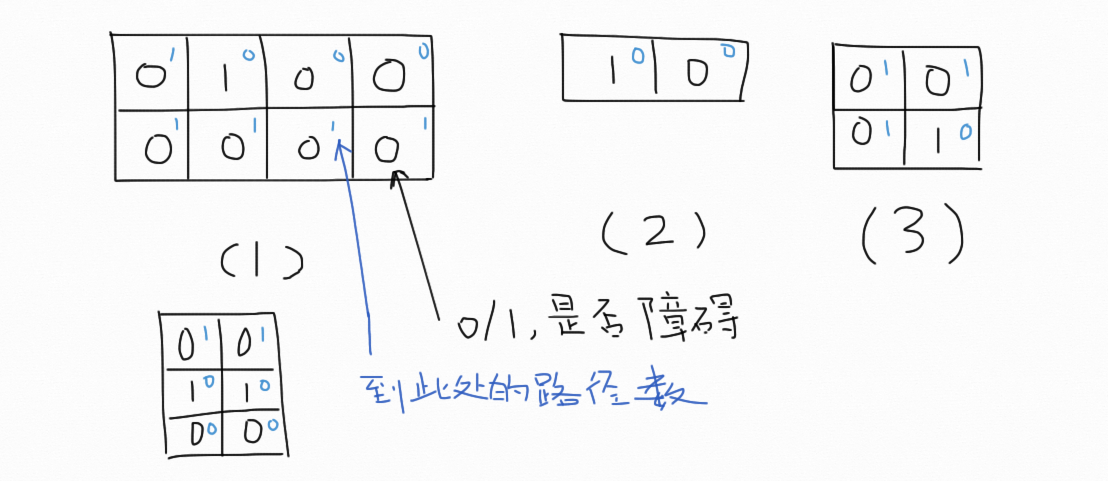
情況（1），在第一行或者第一列中出現了障礙。此時易知，第一行自障礙開始到後面，路徑數都為0（因為此路不通，見(1)的第一行）。第一列同理。

情況（2）（3）則是起點/終點本身無法通過，結果為0。

基於上面的情況，兩步走：

（1）初始值的設定：第一行與第一列，若不為障礙，則設為1，若為障礙，則設為0

先將整個路徑數矩陣dp置為0，然後對第一行/列進行初始化。若不為障礙，則設為1，若為障礙，則設為0，且跳出迴圈，這樣後面的幾個dp值即為初始值0。

        vector<vector<int>> dp (m, vector<int>(n, 0));  // 構造二維陣列儲存每一處的dp值
        for(int i=0; i<m; i++) {                // 為第一列初始化
            if(obstacleGrid[i][0] == 1) {       // 若當前格值為1，則dp值為0，並且之後的值為初始值0
                    // dp[i][0] = 0;        // 初始值即為0，此行可註釋掉
                    break;                // 跳出後，此後的元素則為初始值0
                }
            dp[i][0] = 1;
        }
        for(int i=0; i<n; i++) {            // 第一行，同第一列
            if(obstacleGrid[0][i] == 1) { 
                    // dp[0][i] = 0;
                    break;
                }
            dp[0][i] = 1;
 

        }

（2）dp公式：dp [i] [j] = dp [i-1] [j] + dp [i] [j-1]，進行求解。

        for(int i=1; i<m; i++) {            
            for(int j=1; j<n; j++) {
                if(obstacleGrid[i][j] == 1) {       // 若當前格值為1，則dp值為0
                    dp[i][j] = 0;
                    continue;
                }
                dp[i][j] = dp[i-1][j] + dp[i][j-1];   // 每一處與左側即上側相關。
            }
        }

（3）返回最後一個即為到達右下角的路徑數。

總程式碼：

    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid.size() == 0)
            return 0;
        int m = obstacleGrid.size();    // 行數
        int n = obstacleGrid[0].size(); // 列數
        if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1)  // 起點/終點為1，無法通過，則路徑數為0
            return 0;
        vector<vector<int>> dp (m, vector<int>(n, 0));  // 構造二維陣列儲存每一處的dp值
        for(int i=0; i<m; i++) {                // 為第一列初始化
            if(obstacleGrid[i][0] == 1) {       // 若當前格值為1，則dp值為0，並且之後的值為初始值0
                    // dp[i][0] = 0;        // 初始值即為0，此行可註釋掉
                    break;
                }
            dp[i][0] = 1;
        }
        for(int i=0; i<n; i++) {            // 第一行，同第一列
            if(obstacleGrid[0][i] == 1) { 
                    // dp[0][i] = 0;
                    break;
                }
            dp[0][i] = 1;
        }

        
        for(int i=1; i<m; i++) {            
            for(int j=1; j<n; j++) {
                if(obstacleGrid[i][j] == 1) {       // 若當前格值為1，則dp值為0
                    dp[i][j] = 0;
                    continue;
                }
                dp[i][j] = dp[i-1][j] + dp[i][j-1];   // 每一處與左側即上側相關。
            }
        }
        return dp[m-1][n-1];
    }

優化記憶體使用空間，使用一維陣列即可。

（1）設定初始值：先為第一行進行初始化，若為障礙，則dp值為0，且後續都為0。

（2）DP公式：dp[j] = dp[j-1] + dp[j]。行從第一行開始，列元素從第0個開始。所以要考慮第一列上，若上一個元素為0時的情況。

總程式碼：

    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid.size() == 0)
            return 0;
        int m = obstacleGrid.size();    // 行數
        int n = obstacleGrid[0].size(); // 列數
        if(obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1)  // 起點/終點為1，無法通過，則路徑數為0
            return 0;
        vector<int> dp (n, 0);               // 構造一維陣列儲存dp值
        for(int i=0; i<n; i++) {                // 為第一行初始化
            if(obstacleGrid[0][i] == 1) {       // 若當前格值為1，則dp值為0，並且之後的值為初始值0
                    // dp[i][0] = 0;        // 初始值即為0，此行可註釋掉
                    break;
                }
            dp[i] = 1;
        }

        for(int i=1; i<m; i++) {            
            for(int j=0; j<n; j++) {
                if(obstacleGrid[i][j] == 1) {       // 若當前格值為1，則dp值為0
                    dp[j] = 0;
                    continue;
                }
                if(j == 0) {        // 對於第一列的元素
                    if(dp[j] == 0)  // 若上側為0，則當前也為0
                        continue;
                    dp[j] = 1;
                }
                dp[j] = dp[j-1] + dp[j];   // 每一處與左側即上側相關。
            }
        }
        return dp[n-1];
    }