Tensorflow:1.6.0

優化器（reference:https://blog.csdn.net/weixin_40170902/article/details/80092628）

           I:  tf.train.GradientDescentOptimizer  Tensorflow中實現梯度下降演算法的優化器。

           梯度下降：（1）標準梯度下降GD（2）批量梯度下降BGD（3）隨機梯度下降SGD

           (1)標準梯度下降：學習訓練的模型引數為W，代價函式為J(W)，則代價函式關於模型引數的偏導數即相關梯度為dJ(W)，學習率為eta,梯度下降法更新引數公式：

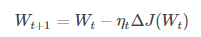
          模型引數的調整沿著梯度方向不斷減小的方向最小化代價函式。基本策略：在有限視野內尋找最快下山路徑，每邁出一步參考當前位置最陡的梯度方向，從而決定下一步。

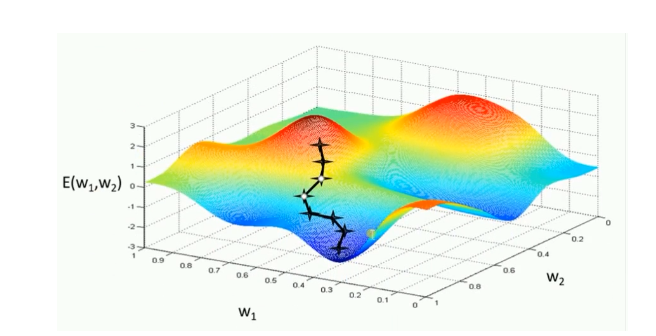
          評價：GD的兩個缺點

                  （1）訓練速度慢：每進行一步都要計算調整下一步方向，在大型資料中，每個樣本都更新一次引數，且每次迭代要遍歷所有樣本，需要很長時間進行訓練和達到收斂。

                  （2）易陷入區域性最優解：在有限的範圍內尋找路徑，當陷入相對較平的區域，誤認為最低點（區域性最優即鞍點），梯度為0，不進行引數更新。

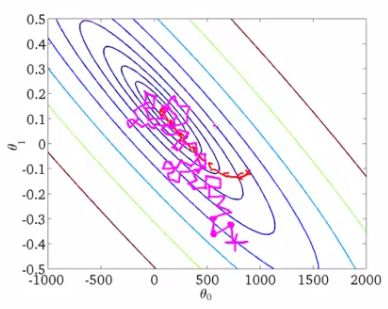
          （2）批量梯度下降BGD：學習訓練樣本的總數為n,每次樣本i形式為（Xi,Yi），模型引數為W，代價函式為J(W)，每個樣本i的代價函式關於W的梯度為dJi（Wt,Xi,Yi），學習率eta_t,跟新引數表示式為：     

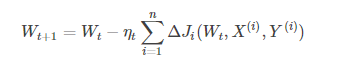          模型引數的更新與全部輸入樣本的代價函式和有關。每次權重的更新發生在批量輸入樣本之後，大大加快訓練速度。

          評價：BGD比GD訓練時間短，而且每次下降的方向都很正確。

#-*- coding: utf-8 -*-
#BGD python 實現
import random
#用y = Θ1*x1 + Θ2*x2來擬合下面的輸入和輸出
#input1  1   2   5   4
#input2  4   5   1   2
#output  19  26  19  20
input_x = [[1,4], [2,5], [5,1], [4,2]]  #輸入
y = [19,26,19,20]   #輸出
theta = [1,1]       #θ引數初始化
loss = 10           #loss先定義一個數，為了進入迴圈迭代
step_size = 0.01    #步長
eps =0.0001         #精度要求
max_iters = 10000   #最大迭代次數
error =0            #損失值
iter_count = 0      #當前迭代次數
 
err1=[0,0,0,0]      #求Θ1梯度的中間變數1
err2=[0,0,0,0]      #求Θ2梯度的中間變數2
 
while( loss > eps and iter_count < max_iters):   #迭代條件
    loss = 0
    err1sum = 0
    err2sum = 0
    for i in range (4):     #每次迭代所有的樣本都進行訓練
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]  #預測值
        err1[i]=(pred_y-y[i])*input_x[i][0]
        err1sum=err1sum+err1[i]
        err2[i]=(pred_y-y[i])*input_x[i][1]
        err2sum=err2sum+err2[i]
    theta[0] = theta[0] - step_size * err1sum/4  #對應5式
    theta[1] = theta[1] - step_size * err2sum/4  #對應5式
    for i in range (4):
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1]   #預測值
        error = (1/(2*4))*(pred_y - y[i])**2  #損失值
        loss = loss + error  #總損失值
    iter_count += 1
    print ("iters_count", iter_count)
print ('theta: ',theta )
print ('final loss: ', loss)
print ('iters: ', iter_count)

           （3）隨機梯度下降法（SGD）：從一批訓練樣本n中隨機選取一個樣本i，模型引數為W，代價函式為J(W)，梯度為dJ(W)，學習率為eta,則使用SGD進行更新引數公式為：

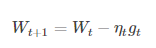
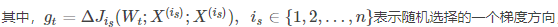
                  SGD不需要每一步都計算梯度，但最終能達到低點，只是過程會比較崎嶇。

          評價：優點：計算梯度快，對於小噪聲，SGD可以很好收斂。對於大型資料，訓練很快，從資料中取大量的樣本算一個梯度，更新一下引數。

                     缺點：在隨機選擇梯度時會引入噪聲，權值更新方向可能出現錯誤。SGD未能克服全域性最優。 

#-*- coding: utf-8 -*-
#SGD-python實現
import random
#用y = Θ1*x1 + Θ2*x2來擬合下面的輸入和輸出
#input1  1   2   5   4
#input2  4   5   1   2
#output  19  26  19  20
input_x = [[1,4], [2,5], [5,1], [4,2]]  #輸入
y = [19,26,19,20]   #輸出
theta = [1,1]       #θ引數初始化
loss = 10           #loss先定義一個數，為了進入迴圈迭代
step_size = 0.01    #步長
eps =0.0001         #精度要求
max_iters = 10000   #最大迭代次數
error =0            #損失值
iter_count = 0      #當前迭代次數
 
while( loss > eps and iter_count < max_iters):    #迭代條件
    loss = 0
    i = random.randint(0,3)  #每次迭代在input_x中隨機選取一組樣本進行權重的更新
    pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1] #預測值
    theta[0] = theta[0] - step_size * (pred_y - y[i]) * input_x[i][0]
    theta[1] = theta[1] - step_size * (pred_y - y[i]) * input_x[i][1]
    for i in range (3):
        pred_y = theta[0]*input_x[i][0]+theta[1]*input_x[i][1] #預測值
        error = 0.5*(pred_y - y[i])**2
        loss = loss + error
    iter_count += 1
    print ('iters_count', iter_count)
print ('theta: ',theta )
print ('final loss: ', loss)
print ('iters: ', iter_count)

          II tf.train.MomentumOptimizer tensorflow中實現動量優化演算法的優化器

           動量優化演算法在梯度下降法的基礎上進行改變，具有加速梯度下降的作用。類別：（1）標準動量優化方法Momentum,(2)NAG動量優化方法（NAG在Tensorflow中與Momentum合併在同一函式tf.train.MomentumOptimizer中，可以通過引數配置啟用。）

         （1）Momentum:引入一個累計歷史梯度資訊動量加速SGD。優化公式如下：

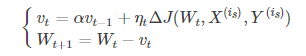
             alpha代表動力大小，一般取為0.9（表示最大速度10倍於SGD）。動量解決SGD的兩個問題：（1）SGD引入的噪聲（2）Hessian矩陣病態（SGD收斂過程的梯度相比正常來回擺動幅度較大）

            當前權值的改變受上一次改變的影響，類似加上了慣性。

         （2）NAG：牛頓加速梯度演算法是Momentum變種，更新公式如下：

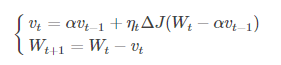
            NAG的計算在模型引數施加當前速度之後，可以理解為在Momentum 中引入了一個校正因子。

            在Momentum中，小球會盲目的跟從下坡的梯度，易發生錯誤。因此，需要提前知道下降的方向，同時，在快到目標點時速度會有所下降，以不至於超出。

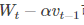     可以表示小球下一個大概的位置，從而知道下一個位置的梯度，然後使用當前位置來更新引數。NGD對凸批量梯度的收斂效果較大，而對NAG的效果作用不大。

           III自適應學習率優化演算法：傳統的優化演算法將學習率設定為常數或者根據訓練次數調節學習率。忽略了學習率其他變化的可能性。（1）AdaGrad(2)RMSProp（3）Adam(4)AdaDelta

           (1)AdaGrad演算法：（tf.train.AdgradOptimizer）

            獨立適應所有模型引數的學習率，縮放每個引數反比於其所有梯度歷史平均值總和的平方根。具有代價函式最大梯度的引數相應的有快速下降的學習率，而小梯度的引數在學習率上有相對較小的下降。

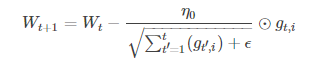
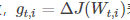g_t,i代表t時刻，指定類別i，代價函式關於W的梯度。對於較高類別的資料，Adagrad給與越來越小的學習率，對於較少的類別資料，給予較大的學習率。Adagrad適用於資料稀疏或者分佈不平衡的資料集。

        評價：優點：無需人為調節學習率，可以自動調節。缺點；隨著迭代次數增多，學習率越來越小，最終趨於0。

           (2）RMSProp演算法(tf.train.RMSPropOptimizer)

            修改了AdaGrad的梯度累積為指數加權的移動平均，使在非凸下效果更好。

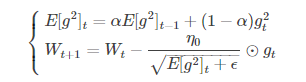
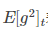代表前t次的梯度平方的均值。RMSProp的分母取了加權平均，避免學習率越來越低，同時可以自適應調節學習率。

          （3）AdaDelta演算法(tf.train.AdadeltaOptimizer)：AdaGrad與RMSProp都需要指定全域性學習率，AdaDelta結合兩種演算法每次引數的更新步長

           評價：在訓練的前中期，表現效果較好，加速效果可以，訓練速度更快。在後期，模型會反覆地在區域性最小值附近抖動。

          （4）Adam演算法(tf.train.AdamOptimizer)：動量直接併入了梯度一階矩（指數加權）的估計。相比於，RMSProp缺少修正因子導致二階矩估計在訓練初期有較高的偏置，Adam包括偏置修正，從原始點初始化的一階矩（動量項）和（非中心的）二階矩估計。

           評價：Adam對超引數的選擇相當魯棒。

不同優化器比較

         下降速度上，三個自適應學習優化器  AdaGrad,RMSProp與AdaDelta的下降速度明顯快於SGD，而Adagrad與RMSProp速度相差不大快於AdaDelta。兩個動量優化器Momentum ,NAG初期下降較慢，後期逐漸提速，NAG後期超過Adagrad與RMSProt。

        在有鞍點的情況下，自適應學習率優化器沒有進入，Momentum與NAG進入後離開並迅速下降。而SGD進入未逃離鞍點。

       速度：快->慢： Momenum ，NAG -> AdaGrad,AdaDelta,RMSProp ->SGD

       收斂： 動量優化器有走岔路，三個自適應優化器中Adagrad初期走了岔路，但後期調整，與另外兩個相比，走的路要長，但在快接近目標時，RMSProp抖動明顯。SGD走的過程最短，而且方向比較正確。