神經網路最基本的元素與計算流程：

基本的組網原則：

神經網路監督學習的基本步驟：

• 初始化權值係數
• 提取一個樣本輸入NN，比較網路輸出與正確輸出的誤差
• 調整權值係數，以減少上面誤差——調整的方法對應不同的學習規則
• 重複二三步，直到所有的樣本遍歷完畢或者誤差在可以容忍的範圍內

Delta規則：（一種更新權值係數的規則）

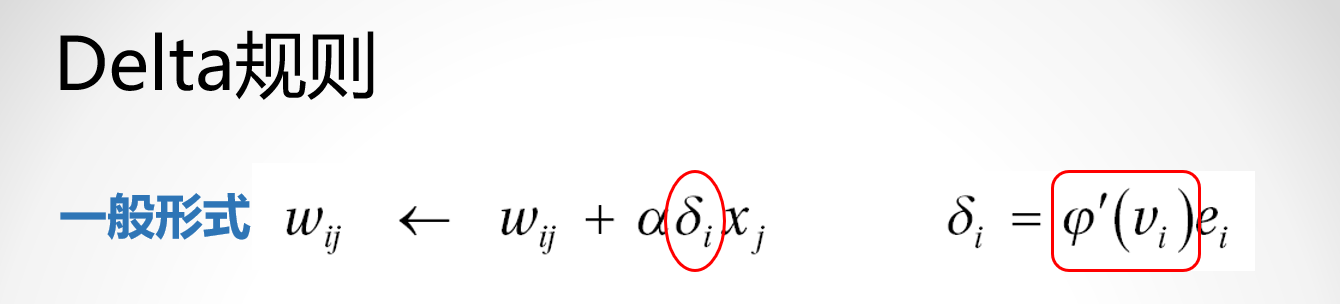
• 基於sigmoid函式的Delta規則：優勢，便於用於分類問題——啟用函式選擇

• 幾種常見權值更新策略：

• 三種更新策略下的程式碼演示

function W = DeltaSGD(W,X,D)
    alpha 
 
= 0.9;
    N = 4;
    for i = 1:N
        x = X(i,:)';
        d = D(i);
        v = W*x;
        y = sigmoid(v);
        e = d - y;
        dy = y*(1-y)*e;
        dW = alpha*dy*x';
        W = dW + W;
    end
end

function W = DeltaBatch(W,X,D)
    alpha = 0.9;
    N = 4;
    dWSum = zeros(1
 
,3);
    for i = 1:N
        x = X(i,:)'; 
        d = D(i);
        v = W*x;
        y = sigmoid(v);
        e = d - y;
        dy = y*(1-y)*e;
        dW = alpha*dy*x';
        dWSum = dWSum + dW;
    end
    dWavg = dWSum/N;
    W = W + dWavg;    
end

function W = DeltaMiniBatch(W,X,D)
    alpha 
 
= 0.9;
    N = 4;
    M = 2;
    for j = 1:(N/M)
        dWSum = zeros(1,3);
        for q = 1:M
            i = j*(M-1) + q;  
            x = X(i,:)';  
            d = D(i);
            v = W*x;
            y = sigmoid(v);
            e = d - y;
            dy = y*(1-y)*e;
            dW = alpha*dy*x';
            dWSum = dWSum + dW;
        end
        dWavg = dWSum/M;
        W = W + dWavg; 
    end
end

function y = sigmoid(x)
    y = 1/(1+exp(-x));
end

function D = DeltaTest()   
    clear all;%清除所有變數
    close all;%關閉所有開啟檔案

    X = [0 0 1;0 1 1;1 0 1;1 1 1];% 輸入樣本
    D = [0 0 1 1];%對應樣本的答案

    % 初始化誤差平方和向量
    E1 = zeros(1000,1);
    E2 = zeros(1000,1);
    E3 = zeros(1000,1);

    % 統一初始化權值係數
    W1 = 2*rand(1,3) - 1;
    W2 = W1;
    W3 = W1;

    % 使用三種方法訓練1000輪 同時每一輪計算一次誤差平方
    for epoch = 1:1000
        %各自完成一輪訓練
        W1 = DeltaSGD(W1,X,D);
        W2 = DeltaBatch(W2,X,D);
        W3 = DeltaMiniBatch(W3,X,D);

        % 計算這一輪結束後的誤差平方
        N= 4;
        for i = 1:N
            %利用誤差計算方法計算誤差
            % E1
            x = X(i,:)';
            d = D(i);
            v1 = W1*x;
            y1 = sigmoid(v1);
            E1(epoch) = E1(epoch) + (d - y1)^2;

            % E2
            v2 = W2*x;
            y2 = sigmoid(v2);
            E2(epoch) = E2(epoch) + (d - y2)^2;

            % E3
            v3 = W3*x;
            y3 = sigmoid(v3);
            E3(epoch) = E3(epoch) + (d - y3)^2;
        end

    end
    for i = 1:4
        x = X(i,:)';d = D(i);
        v = W1*x;
        y = sigmoid(v)
    end
    % 繪製三種演算法策略的差異圖
    plot(E1,'r');hold on
    plot(E2,'b:');
    plot(E3,'k-');
    xlabel('Epoch');
    ylabel('Sum of Squares of Training Error');
    legend('SGD',"Batch",'MiniBatch');
end