文章目錄

• 答案
• 解析
• 選擇題
• 不定項
• 問題求解
• 讀程式
• 完善程式

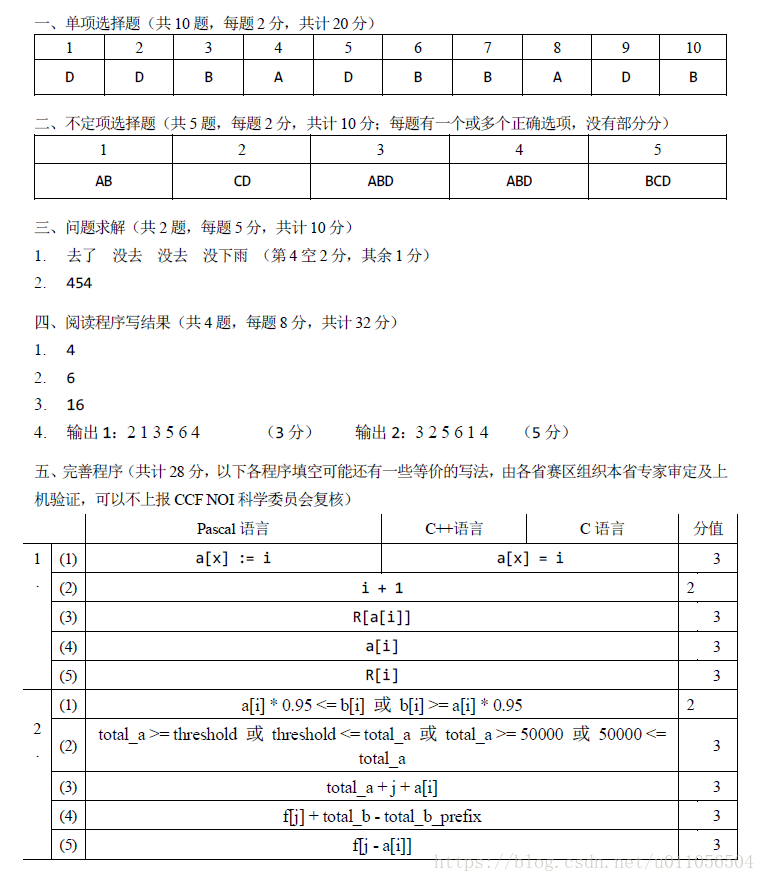
答案

解析

解析全是我的個人想法（胡扯），有大佬發現錯漏的請麻煩指出。

選擇題

不是說好15題1.5分每題的嗎？
第一題直接算就好了吧，D是619，其他都是617

第二題我猜的，C/C++/Pascal感覺差不多是一類，於是就選Python
貼一個百度連結，自己看吧

第三題說什麼好呢，不過應該可以記得冬令營的時候雅禮門口大大的35th。然而這題我做錯了。

第四題將h=1和h=2並隨便去一個k帶入就會發現只有A是正確的。當然感受一下或者類似二叉樹的理解一下也能理解出來A是對的。

第五題顯然T(n)就是從1加到n，這個顯然是 $n^2$級別的。

第六題沒話說，該怎樣怎樣。

第七題有人要我寫一下詳細的過程（感覺我這個做法很蠢，應該有更高明的做法）：
假設可以把這條線段分成n段，每段的長度是 $\frac{1}{}$

第八題我錯了，我選的是C，正確答案是A（看錯題了）。
直接帶個3或者4進去暴力做一下就能選出A。
當然直接從意義上去考慮推也行，自行百度吧。

第九題是不是又要推式子……（我的做法又好蠢）
紅球每個人都會抽一個。
藍球設每個人抽S個：
n趨於正無窮。
$S={0\over 2^1}+{1\over 2^2}+{2\over 2^3}+...+{n-1\over 2^n}$
${S\over 2}={0\over 2^2}+{1\over 2^3}+{2\over 2^4}+...+{n-2\over 2^n}+{n-1\over 2^{n+1}}$