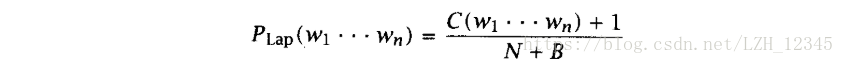一、n-gram模型概念

n-gram模型也稱為n-1階馬爾科夫模型，它有一個有限歷史假設：當前詞的出現概率僅僅與前面n-1個詞相關，可以表示為：

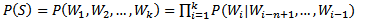
    當n取1、2、3時，n-gram模型分別稱為unigram、bigram和trigram語言模型。n-gram模型的引數就是條件概率P(Wi|Wi-n+1,...,Wi-1)。假設詞表的大小為100,000，那麼n-gram模型的引數數量為100,000n。n越大，模型越準確，也越複雜，需要的計算量越大。最常用的是bigram，其次是unigram和trigram，n取≥4的情況較少。

二、n-gram模型的引數估計

模型的引數估計也稱為模型的訓練，n-gram模型的引數的估計表示式如下：

一般採用最大似然估計（Maximum Likelihood Estimation，MLE）的方法對模型的引數進行估計：

舉個例子來說明一下，IBM Brown利用366M英語語料訓練trigram，結果在測試語料中，有14.7%的trigram和2.2%的bigram在訓練中沒有出現；根據博士期間所在的實驗室統計結果，利用500萬字人民日報訓練bigram模型，用150萬字人民日報作為測試語料，結果有23.12%的bigram沒有出現。這種問題也被稱為資料稀疏（Data  Sparseness），解決資料稀疏問題可以通過資料平滑（Data Smoothing）技術來解決。

三、平滑演算法

資料平滑是對頻率為0的n元對進行估計，典型的平滑演算法有加法平滑、Good-Turing平滑、Katz平滑、插值平滑等。

3.1 加法平滑

3.1.1  Laplace法則（加1平滑）

通過給每個n元組都加1，實現將一小部分概率轉移到未知事件上，公式如下：

3.1.2  Lidstone 法則

3.2  Good-Turing估計

3.3 Katz回退演算法

3.4. 線性插值

四、arpa檔案的各部分引數詳解