內容提要

• 引言
• MP特徵選擇思想
• MP特徵選擇演算法
• MP特徵選擇分析
• 實驗結果
• 分析總結

引言

  一般選擇文字的片語作為分類器輸入向量的特徵語義單元，而作為單詞或詞語的片語，在任何一種語言中都有數萬或數十萬個。另外，對於Web文字檢索應用來說，網際網路每天可能都會產生各種各樣的新詞彙。這樣文字分類問題就面臨著特徵向量的維數災難問題。有許多理由要求必須將特徵的數量減少到儘可能的小，其中時間和空間複雜度就是很重要的理由。另一方面，雖然兩個特徵可能具有很好的分類資訊，但是當把它們合併成一個特徵時，由於相關性，分類資訊可能丟失。設計分類器不僅要保證分類正確率，還要保證其分類效能。特徵選擇的任務就是：在給定的片語中，選擇具有重要分類資訊而又能減少特徵的片語作為分類文字的特徵。特徵選擇的過程也是特徵壓縮的過程，如果選擇的特徵不具有分類識別能力，那麼將會設計出得到分類效果很差的分類器。另一方面，如果選擇的特徵能夠很好的保留分類資訊，除去那些幾乎不能識別類別的片語，將在很大程度上簡化分類器的設計。

MP特徵選擇思想

  對於刪除標點符號和停用的片語表示的文字，其中的片語具有不同的類別識別能力。本文提出一種基於矩陣投影(Matrix Projection，MP)運算的特徵選擇方法。矩陣投影特徵選擇方法是基於概率模型，綜合考慮片語的文件頻率以及片語在單個類別下的平均詞頻進行特徵選擇。這裡的文件頻率不是整個訓練資料集的文件頻率，而是一個片語在摸個類別下的文件頻率，即該片語在一個類別下出現的文字數量比上該類別文字總數。詞頻為一篇文字中某詞出現的次數比上該文字的總詞數。平均詞頻是一個詞在該類別下每一篇文字中的詞頻的算術平均。特徵提取的過程：對已標註的訓練語料，統計片語在類別中的文件頻率 ,以及特徵項在類別中每一個文件的詞頻 。通過投影函式計算片語在類別中的矩陣投影結果。根據運算結果的大小進行特徵選擇，最終選取那些結果值比較大的片語作為分類的特徵。

MP特徵選擇演算法

  下面通過定義矩陣投影運算逐步引出MP特徵選擇過程。首先給出矩陣投影的一般定義如下。
  定義 ：矩陣投影：設 A 是一個mxn 的矩陣，即 A_mXn=(a_ij)_mXn，矩陣中各元素間相互獨立。投影運算過程如圖1所示:

圖1 矩陣投影運算過程

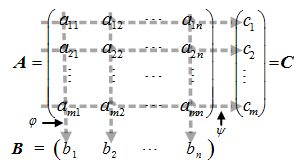
矩陣 A 通過投影運算得到 1Xn 的矩陣 B 和 的矩陣 C :

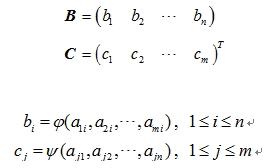
矩陣 B 和矩陣 C 稱為矩陣 A 的投影。其中矩陣B是矩陣A的垂直投影， φ(a_1i,a_2i,…,a_mi) 叫做垂直投影函式；矩陣 C 是矩陣 A 的水平投影， ψ(a_j1,a_j2,…,a_jn) 叫做水平投影函式。
  上述運算得到的投影具有如下性質。
  性質

：矩陣 A 中的每一行與每一列元素組成的向量都是不相關的。考慮垂直投影，矩陣 B 與矩陣 A 中的每一行元素組成的向量是相關的。通過垂直投影函式φ(a_1i,a_2i,…,a_mi) 建立了矩陣 A 的每一列元素的相關性。水平投影具有類似性質，通過水平投影函式 ψ(a_j1,a_j2,…,a_jn) 建立了矩陣 A 的每行元素的相關性。
  投影運算是本文提出的一種特徵選擇矩陣壓縮演算法。通過垂直投影，將矩陣的一列元素(同一個片語在不同文件中的詞頻)攜帶的片語相關的頻率資訊壓縮到投影向量的一個元素中，建立一類文件向量空間中片語之間的聯絡。水平投影的意義是將一篇文件中的不同片語的資訊壓縮到行向量的一個元素中。本文主要應用垂直投影運算進行特徵選擇。
  本文描述的文字分類特徵選擇演算法就是利用上述矩陣的垂直投影運算建立類別c_i 中各文件片語之間的關聯性，構建投影特徵向量。通過計算投影矩陣中作為元素的片語的投影運算結果大小，決定片語的去留，進行特徵的選擇。考慮已標註訓練資料集類別c_i 下，各文件的片語詞頻的向量空間表示形式如下式所示:

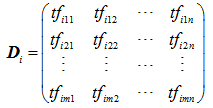
  其中： tf_ijk 表示片語t_k 在類別c_i 中某個文件j中的詞頻；
       1≤i≤p，p 表示訓練集類別的數量；
       1≤j≤m，m 表示訓練集類別c_i 中文字的數量；
      1≤k≤n，n 表示訓練集類別c_i 中文字含有片語的總數量；
  矩陣 D_i 中每一行表示一篇文件，每一列表示一個片語在不同文件中的詞頻。矩陣 D_i 通過垂直投影函式 φ ，運算得到矩陣 V_i = (v_i1,v_i2,…,v_in)，其中 v_ik=φ(tf_i1k,tf_i2k,…,tf_imk) ，我們稱其為投影值。 V_i 是 1Xn 的矩陣，即 n 維向量。
  投影值的計算是考慮片語在資料集中單一類別中的文件頻率和詞頻率的平均值。垂直投影函式 φ 形式化表示如式:

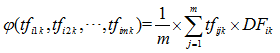
計算 φ(tf_i1k,tf_i2k,…,tf_imk) 文件頻率 DF_ik 是類別 c_i 中片語 t_k 的文件頻率，表示形式如下式所示：

其中：

將下述兩式帶入 φ 函式得到最終求解投影值如式所示：

  計算出所有片語的投影值 v_ik，就可以從投影值所表示的向量 V_i = (v_i1,v_i2,…,v_in) 中進行特徵選擇。特徵選擇選取那些投影值 v_ik 最大的N項片語作為分類特徵。

MP特徵選擇分析

  為了形象的描述MP特徵選擇與卡方校驗、資訊增益、文件頻率和互資訊特徵選擇結果的不同，本文做一個小實驗進行說明。
  實驗資料集為TanCorpV1.0中抽取的兩個類別，分別是“汽車”和“電腦”，每個類別下選取100篇文件。通中文過分詞之後，選取其中有兩個漢字組成的詞作為特徵選擇的備選片語，其中共有3322個不同的片語。分別採用上述五種特徵選擇方法進行特徵選擇，都選擇100個片語作為特徵。特徵選擇的結果如表1和圖2所示。在圖或表中u 表示“汽車”類，v表示“電腦”類。

表1 五種特徵選擇各類別特徵分佈表

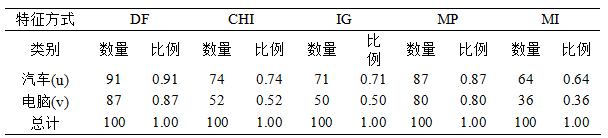
  表1中數量代表選出的100個特徵在相應類別下面出現的個數，比例為所佔的特徵比例，即選出的相應類別下選出的特徵站總特徵的比例。例如文件頻率(DF)選擇的100個特徵中，其中有91個在“汽車”類(u)中出現，佔總特徵的比例為0.91；87個特徵在“電腦”類(v)中出現，佔總特徵的比例為0.87。

圖2 五種方法選擇出的特徵隨詞頻分佈圖

  圖2橫軸表示片語的編號，將3322個詞分別按照出現的次數從1開始編號到3322。例如出現最多的詞“公司”，在200篇文字中共出現了97次，因此“公司”被編號為1，以此類推。編號前5的詞其餘四個分別是“病毒”出現83次、“中國”出現82次、“手機”出現71次、“交通”出現62次。詞的序號越大詞頻越低，也就是出現的次數越少，其中僅出現1次的詞就有1532項。縱軸分別表示五種特徵選擇選出的兩個類別下的特徵，符號即代表相應特徵的出現。以DF說明，DF-u對應的是DF特徵選擇選出的詞出現的情況，某詞出現就在片語序號對應位置用符號標示出來。我們只關注圖中特徵的整體分佈，不去關注具體的某一個特徵。
  從表1中可以看出DF選擇的特徵在類別之間最沒有差別，兩個類別中重複詞數高達78個。MI選擇的特徵在類別之間最有差別，兩個類之間沒有重複出現的詞。CHI和IG選擇的特徵差異性也較大，重複的詞分別只有26個和21個。MP選擇的特徵差異性也較小，重複詞數為67個。
  從圖2中可以觀察到,DF選擇的都是高頻詞。CHI和IG選擇的特徵分佈比較廣，並且在低頻詞類別之間的特徵幾乎沒有重複的，也就是區分度較好；並且二者選擇的特徵很相近。MI現在的特徵在中頻段分佈比較均勻，但是相對低頻的詞被選為特徵的較多，這也驗證了互資訊“依賴低頻詞”的弊端。MP選擇的特徵不僅差異性比DF好，而且更接近高頻詞，這樣分類更容易命中詞，不像MI，很容易造成難命中低頻詞問題，造成分類效果不理想。
  MP特徵選擇演算法，不考慮類別之間的詞的差異，只考慮單個類別中出現的最普遍的詞。我們的假設：在不同類別內部同時出現的高頻詞都提供相同的分類資訊，或低效類別區分能力，不影響分類。

實驗結果

1. 四種特徵選擇方法在kNN演算法上的分類精度如圖3所示：

圖3 20_Newsgroups上四種特徵選擇下的kNN演算法分類精度

2. 四種特徵選擇方法在貝葉斯(MNNB)演算法上的分類精度如圖4所示：

圖4 TanCorpV1.0上四種特徵選擇下的MNNB演算法分類精度

3. 四種特徵選擇方法在SVM演算法上的分類精度如圖5所示：

圖5 SogouC20000上四種特徵選擇下的SVM演算法分類精度

分析總結

  通過上述實驗結果可見，MP特徵選擇演算法應用於各種分類演算法都能取得比較好的分類效果。MP方法比DF方法優勢明顯，並且略優於或等於CHI與IG特徵選擇方法的分類效果。

參考文獻：
[1] Sebastiani，F. Machine learning in automated text categorization [J]. ACM Comput. Surv. 34(1): 1-47.
[2] 郝秀蘭，陶曉鵬，王述雲，徐和祥，胡運發.基於特徵選擇及Condensing技術的文字取樣[J].模式識別與人工智慧，22（5)：709-717.
[3] Jain，A.K.，Zongker，D. Feature selection: Evaluation, application, and small sample performance [J]. IEEE Trans. on Pattern Analysis and Machine Intelligence，19(2)：153−158.
[4] 朱靖波，王會珍，張希娟.面向文字分類的混淆類判別技術[J].軟體學報，2008，19(3):630-639.