20172314 2018-2019-1《程式設計與資料結構》第八週學習總結
教材學習內容總結
堆
- 堆:是一顆完全二叉樹,每一個結點都小於等於左右孩子(最小堆),或大於等於左右孩子(最大堆)他的每一個子樹也是最小堆或最大堆。
- 堆的操作
- addElement操作(堆的插入)
- 插入新結點時,是作為葉子結點插入的,且一定要保持樹的完整性。如果最下層不滿,插入到左邊的下一個空位,如果最底層是滿的,插入到新一層的左邊第一個位置。
- 如果插入的數相對樹而言較小,則需要在插入後進行重排序

- removeMin方法(堆的刪除)
- 由於最小元素儲存在根處,為了維持樹的完整性,那麼只有一個能替換根的合法元素,且它是儲存在樹中最末一片葉子上的元素(將是樹中h層上最右邊的葉子)。
- 將替換元素移到根部後,必須對該堆進行重排序。
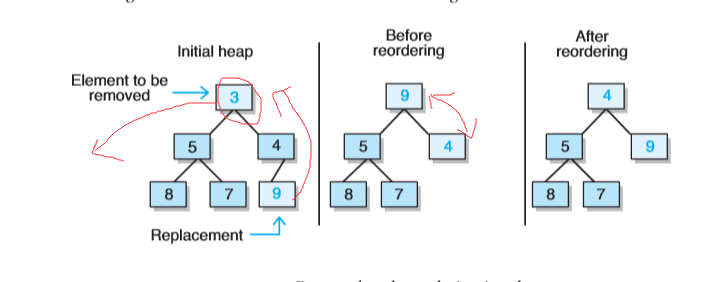
- findMin操作
- 這個方法需要返回在最小堆中最小元素的引用,由於最小堆中最小元素在根處,所以只需返回根部元素即可。
使用堆:優先順序佇列
- 具有更高優先順序的專案在先。
- 具有相同優先順序的專案使用先進先出的方法來確定其排序。
- 雖然最小堆不是一個佇列,但它提供了一個高效的優先順序佇列實現。
用連結串列實現堆
- 由於要求插入元素後能夠向上遍歷樹,所以堆結點中必須儲存指向雙親的指標。
- 由於BinaryTreeNode類沒有雙親指標,所以要建立一個HeapNode類開始連結串列實現。
- addElement操作
- 在適當位置新增一個新元素
- 對堆進行重排序以維持其排序屬性
- 將lastNode指標重新設定為指向新的最末結點
- 在這個方法中用到了getNextParentAdd方法(返回指向某結點的引用,該結點為插入結點的雙親),還有一個heapifyAdd方法,(完成對堆的任何重排序,從新葉子開始向上處理至根處)
- addElement操作有三步
- 首先要確定插入結點的雙親(從堆的右下結點往上遍歷到根,再往下遍歷到左下結點,時間複雜度為2*logn)
- 其次是插入新結點(只涉及簡單的賦值語句,時間複雜度為O(1))
- 最後是從被插入葉子處到根處的路徑重排序,來保證堆的性質不被破壞(路徑長度為logn,最多需要logn次比較)
- 因此addElement操作的複雜度為2*logn+1+logn,即為O(logn)
- removeMin操作
- 用最末結點處的元素替換根處元素
- 對堆進行重排序
- 返回初始的根元素
- addElement操作
用陣列實現堆
- 陣列相比於連結串列,優點是不需要遍歷來查詢最末一片葉子或下一個插入結點的雙親,直接檢視陣列的最末一個元素即可。
- 在陣列中,樹根存放在0處,對於每一個結點n,n的左孩子位於陣列2n+1處,n的右孩子位於陣列的2(n+1)處。同樣,反過來查詢時,對於任何除了根之外的結點,n的雙親位於(n-1)/2位置處。
- addElement操作
- 在恰當位置處新增新結點
- 對堆進行重排序以維持其屬性
- 將count遞增1
- 只需要一個heapifyAdd方法進行重排序,不需要重新確定新結點雙親位置。此方法的時間複雜度是O(logn)
- removeMin操作
- 用最末元素替換根元素
- 對堆進行重排序
- 返回初始根元素
- 由於末結點儲存在陣列的count-1位置處,所以不需要確定最新末結點的方法,此方法複雜度為O(logn)
- findMin操作
僅僅返回根處元素即可,就是陣列的位置0處,複雜度為O(1)
使用堆:堆排序
- 堆排序的過程(由兩部分構成,新增和刪除)
- 將列表的每一元素新增到堆中
- 一次一個將他們從根刪除,再次存放到陣列中
- 最小堆時得到的排序結果是升序,最大堆時得到的排序結果是降序
- 對於每一個結點來說,新增和刪除操作的複雜度都是O(logn),所以對於有n個結點的堆來說,複雜度是O(nlogn)
- 堆排序的複雜度具體分析
- 堆化過程一般是用父節點和他的孩子節點進行比較,取最大的孩子節點和其進行交換;但是要注意這應該是個逆序的,先排序好子樹的順序,然後再一步步往上,到排序根節點上。然後又相反(因為根節點也可能是很小的)的,從根節點往子樹上排序。最後才能把所有元素排序好。對於每個非葉子的結點,最多進行兩次比較操作(與兩個孩子)因此複雜度為2*n
- 排序過程就是把根元素從堆中刪除,刪除每個元素複雜度為logn,對所有元素來說,複雜度為nlogn。
- 所以是2*n + nlogn,複雜度是O(nlogn)

教材學習中的問題和解決過程
- 問題一:getNextParentAdd方法的程式碼理解
問題一解決:
* 第一種情況
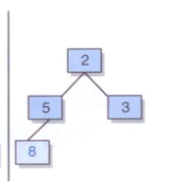
首先考慮while迴圈,result為8,他是左孩子,所以不進入while迴圈,接著往下,他不是根結點,他不是父結點的右孩子,所以result為父結點5,即返回的插入結點的雙親。
* 第二種情況
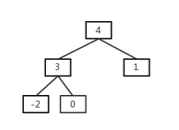
result為0,雙親結點的左孩子為-2,所以進入while迴圈,result為3,接下來進入if語句,他不是根結點,而且父結點的右孩子(1)不為空,所以返回的插入結點的雙親結點是1
* 第三種情況
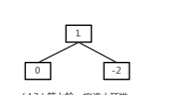
while迴圈中,result(2)不是左孩子,所以result為雙親結點1,往下,他是根結點,而且左子樹不為空,result為左孩子0.這種情況就相當於滿樹時插入到新一層的左邊位置。private HeapNode<T> getNextParentAdd() { HeapNode<T> result = lastNode;// 當前的空白結點 while ((result != root) && (result.getParent().getLeft() != result))//如果當前不是一個滿堆,他不是左孩子 result = result.getParent(); if (result != root) { // /不是一個滿堆 if (result.getParent().getRight() == null)//右邊是空位 result = result.getParent(); else {//右邊不空 result = (HeapNode<T>) result.getParent().getRight(); // 不斷的向下尋找最後的父結點 while (result.getLeft() != null) result = (HeapNode<T>) result.getLeft(); } } else {// 當前堆是一個滿堆 while (result.getLeft() != null) result = (HeapNode<T>) result.getLeft(); } return result; }- 問題二:heapifyAdd方法的程式碼理解
問題二解決:舉個例子,
private void heapifyAdd() { T temp; HeapNode<T> next = lastNode; temp = next.getElement(); while ((next != root) && (((Comparable) temp) .compareTo(next.getParent().getElement()) < 0)) { next.setElement(next.getParent().getElement()); next = next.parent; } next.setElement(temp); }
如圖在樹中插入結點2,那麼next指向2,temp=2,這時next不是根結點,並且2(temp)比4(next.getParent().getElement())小,所以現在next的值設定為4(即原來2的那個位置變成4),next指向原來next的父親結點(即原來的4位置),然後將next的值設為temp即2(原來4的位置變為2),這樣就將2和4換位,實現了重排序。- 問題三:堆排序的過程
問題三解決:首先把待排序的元素在二叉樹位置上排列,然後調整為大頂堆或小頂堆,接下來進行排序,以小頂堆為例,根結點為最小,所以拿掉根,然後對堆進行調整,使其符合小頂堆的要求,然後新的堆頂又是最小的,將其拿掉,如此迴圈...藍墨雲關於這個的測試題,重新梳理一下如圖,大頂堆的過程與其類似,但注意在程式碼實現中,小頂堆排序結果為升序,大頂堆排序結果為降序
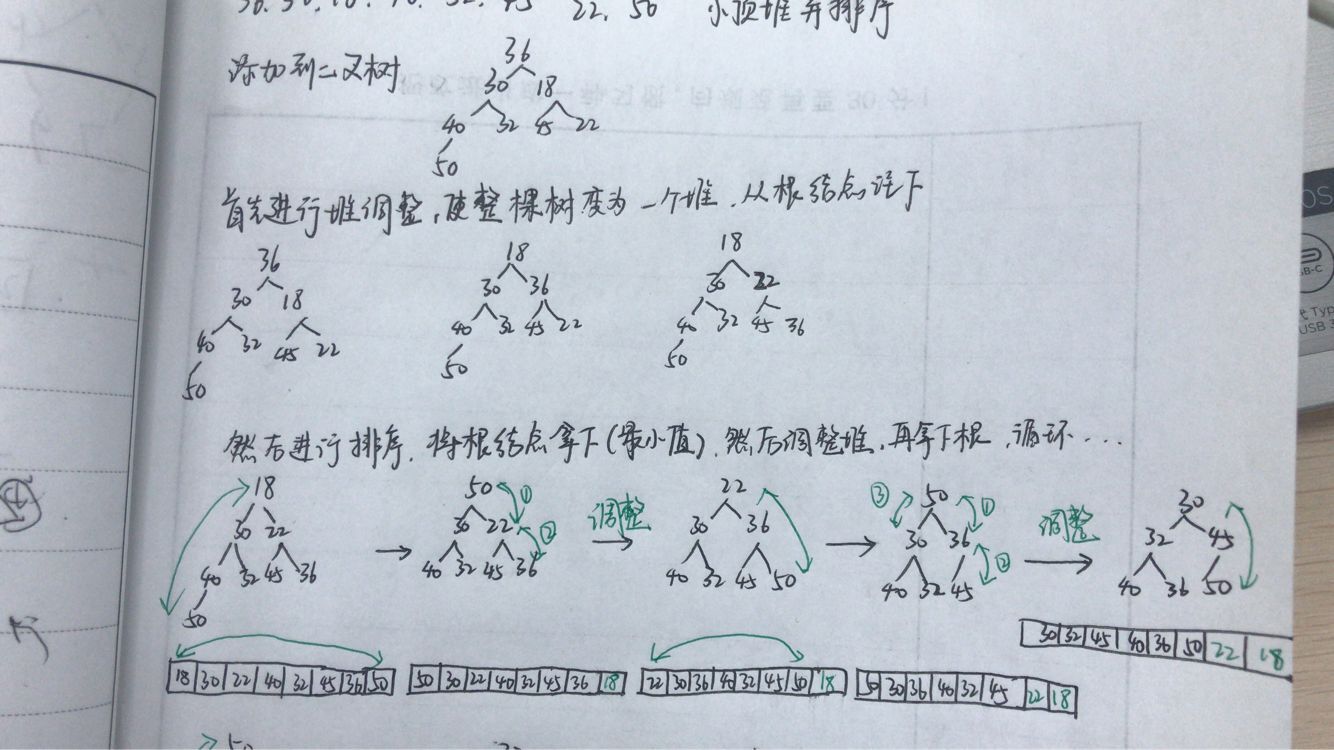
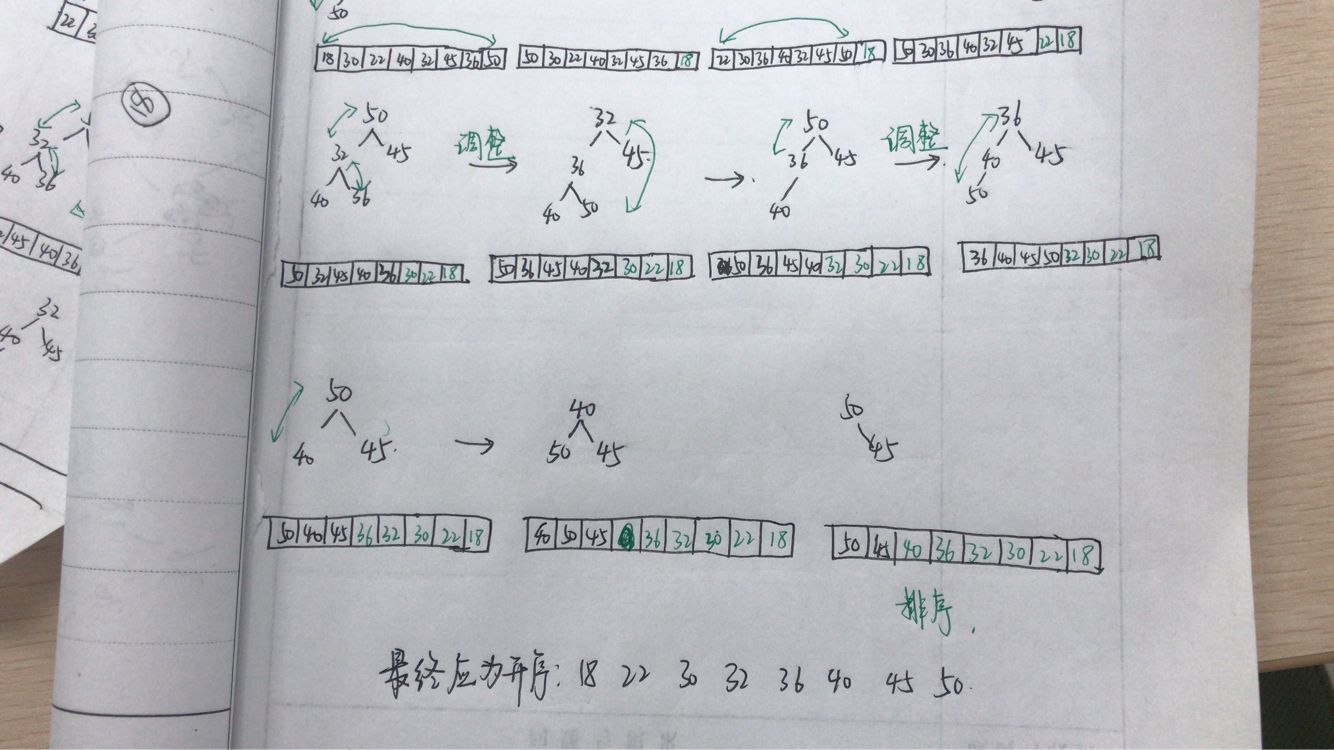
- 問題四:對於優先順序佇列的理解
- 問題四解決:佇列是一種特徵為FIFO的資料結構,每次從佇列中取出的是最早加入佇列中的元素。但是,許多應用需要另一種佇列,每次從佇列中取出的應是具有最高優先權的元素,這種佇列就是優先順序佇列。優先順序佇列的特點:
- 優先順序佇列是0個或多個元素的集合,每個元素都有一個優先權或值。
- 當給每個元素分配一個數字來標記其優先順序時,可設較小的數字具有較高的優先順序,這樣更方便地在一個集合中訪問優先順序最高的元素,並對其進行查詢和刪除操作。
- 在最小優先順序佇列(min Priority Queue)中,查詢操作用來搜尋優先順序最小的元素,刪除操作用來刪除該元素。在最大優先順序佇列(max Priority Queue)中,查詢操作用來搜尋優先順序最大的元素,刪除操作用來刪除該元素。
- 每個元素的優先順序根據問題的要求而定。當從優先順序佇列中刪除一個元素時,可能出現多個元素具有相同的優先權。在這種情況下,把這些具有相同優先權的元素按先進先出處理。
程式碼除錯中的問題和解決過程
問題一:在做藍墨雲測試構造大頂堆並排序時,對於過程的輸出結果是每次將最大數從堆頂拿下時的結果,並不是顯示每次排序時的陣列情況。
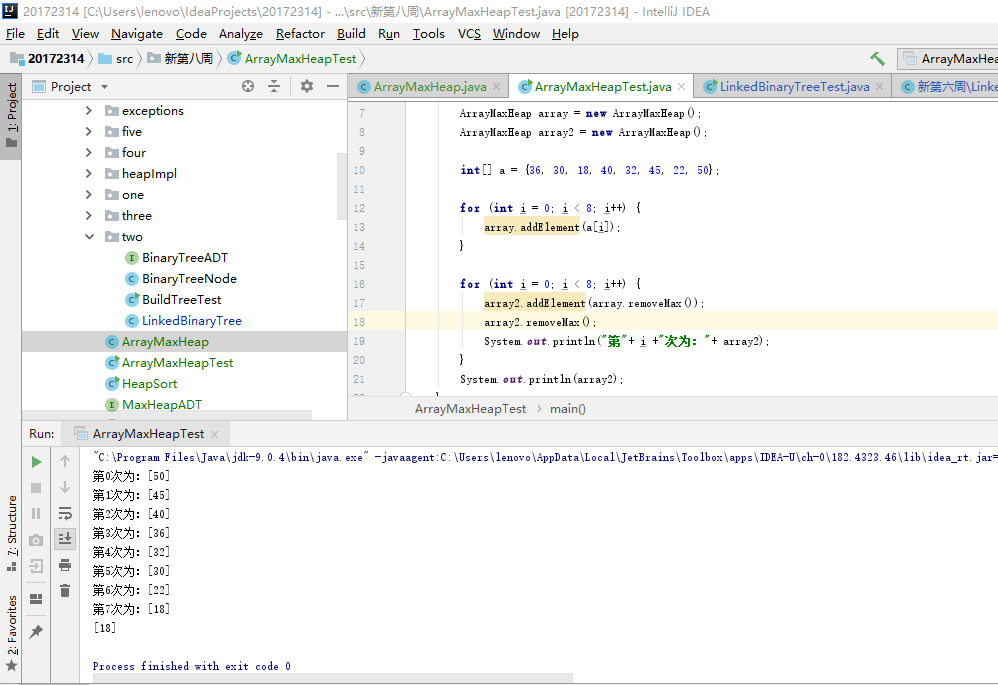
問題一解決:主要錯誤之處在於測試類,如圖中顯示,我的過程記錄是
for(int i=0;i<8;i++){ array2.addElement(array.removeMax); array2.removeMax(); System.out.println("第"+i+"次為:"+ array2); }首先,在迴圈中array中每次拿掉的最大數新增到array2中,然後輸出的是array2中的最大數,那麼就相當於每次把array中的最大數輸出,array2沒有什麼作用。應該為
這樣就把array2的作用發揮出來了,array2中存放array中依次彈出的最大數,在array2中降序排列,然後每次輸出array陣列,顯示現在陣列情況,排序的結果就可以用類似上面的for迴圈依次將array2中的數輸出。for (int i = 0; i <a.length; i++) { array2[i]=array.removeMax(); System.out.println("第"+ i +"次為:"+ array); }- 問題二:在做PP12.1時,對於優先順序佇列的輸出情況理解有問題。
問題二解決:測試類通過在迴圈中使用
queue.removeNext()方法,是由於PriorityQueue類中removeNext方法繼承了ArrayHeap類中的removeMin方法,而在ArrayHeap類中,removeMin又使用了方法heapModifyRemove,其中else if (((Comparable)tree[left]).compareTo(tree[right]) < 0) next = left當left比right小時,返回左,我最開始不理解的是在優先順序佇列中,當優先順序相同時
if (arrivalOrder >obj.getArrivalOrder())//優先順序相同時,先進先出 result = 1;應返回左邊的arrivalOrder,但在heapModifyRemove中來說,卻返回compareTo右邊的,所以我覺得矛盾,進行多次測試後我發現輸出的結果沒有錯。又仔細看程式碼之後發現,優先順序相同時,返回1的情況是arrivalOrder較大,那麼就代表它是後進的,並不是跟優先順序一樣大的先,arrivalOrder越大代表晚進,應該後出,所以正好反一下。
問題三:實現ArrayHeap類時,發現輸出結果總是多一個數
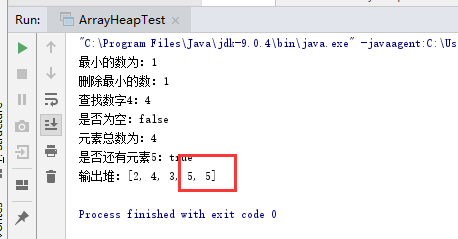
問題三解決:參考了譚鑫同學的部落格,裡面提到了解決辦法,如圖
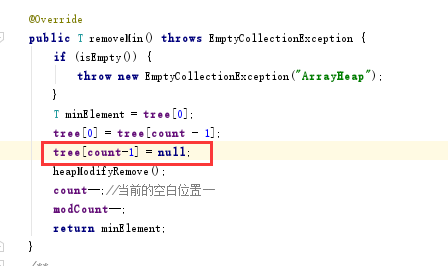
新增語句之後解決問題,原因是在將根結點拿掉並用末葉子結點替換後並沒有將葉結點刪除,所以導致出現兩次,新增語句tree[count-1] = null;之後,將其值設定為空,相當於刪除。
程式碼託管
上週考試錯題總結
錯題一:
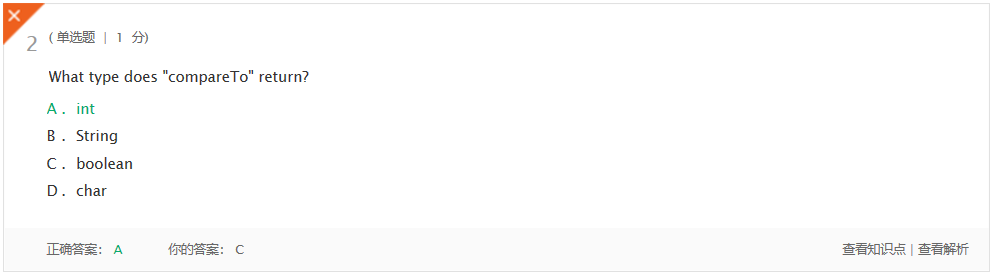
錯題一解決:CompareTo方法返回值是int型的,如果前者比後者大的話返回1,小的話返回-1,相等返回0.
結對及互評
- 20172305譚鑫:譚鑫的部落格中提到的”問題1:實現優先順序佇列的二叉堆、d堆、左式堆、斜堆、二項堆都是什麼意思?和最小堆、最大堆有什麼區別?”是我沒有學習過的,學習到了左式堆,二項堆,斜堆等堆。同時參考他的部落格解決了一個程式碼問題,非常有價值。
- 20172323王禹涵:王禹涵的部落格對程式碼的解釋很詳盡,排版精美,很舒適。
其他
這一章感覺原理很容易理解,邏輯簡單,但用程式碼實現不好理解,但是書上程式碼的可用性很高,然後實驗方面也花費較長時間,總結出來就是要儘早去掌握核心程式碼再開展學習。
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | |
|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 |
| 第一週 | 0/0 | 1/1 | 8/8 |
| 第二週 | 1163/1163 | 1/2 | 15/23 |
| 第三週 | 774/1937 | 1/3 | 12/50 |
| 第四周 | 3596/5569 | 2/5 | 12/62 |
| 第五週 | 3329/8898 | 2/7 | 12/74 |
| 第六週 | 4541/13439 | 3/10 | 12/86 |
| 第七週 | 1740/15179 | 1/11 | 12/97 |
| 第八週 | 5947/21126 | 1/12 | 12/109 |
