20172308 《程式設計與資料結構》第八週學習總結
教材學習內容總結
第 十二 章 優先佇列與堆
一、堆:具有兩個附加屬性的一顆二叉樹
- 它是一顆完全樹
- 對每一結點,它小於或等於其左右孩子(或大於等於其左右孩子)
最小堆:對每一結點,它小於或等於其左右孩子
最大堆:對每一結點,它大於或等於其左右孩子
最小堆將其最小元素儲存在二叉樹的根處,且其根的兩個孩子同樣也是最小堆
最大堆將其最大元素儲存在二叉樹的根處,且其根的兩個孩子同樣也是最大堆
堆是二叉樹的擴充套件,繼承了二叉樹的所有操作
- addElement操作
- addElcment方法將給定的元素新增到堆中的恰當位置處,且維持該堆的完全性屬性和有序屬性
- 如果給定元素不是 Comparable的,則該方法將丟擲一個 ClasscastException異常。
- 完全屬性是指:如果一棵二又樹是平衡的,即所有葉子都位於h或h-1層,其中h為log2 n,且n是樹中的元素數目,以及所有h層中的葉子都位於該樹的左邊,那麼該樹就被認為是完全的
- 增加元素的兩種可能性(如圖):
因為一個堆就是一棵完全樹,所以對於插入的新結點而言只存在一個正確的位置:
要麼是h層左邊的下一個空位置(即最後一層未滿,將插入到最左邊的位置)
要麼是h+1層左邊的第1個位置(如果h層已滿)
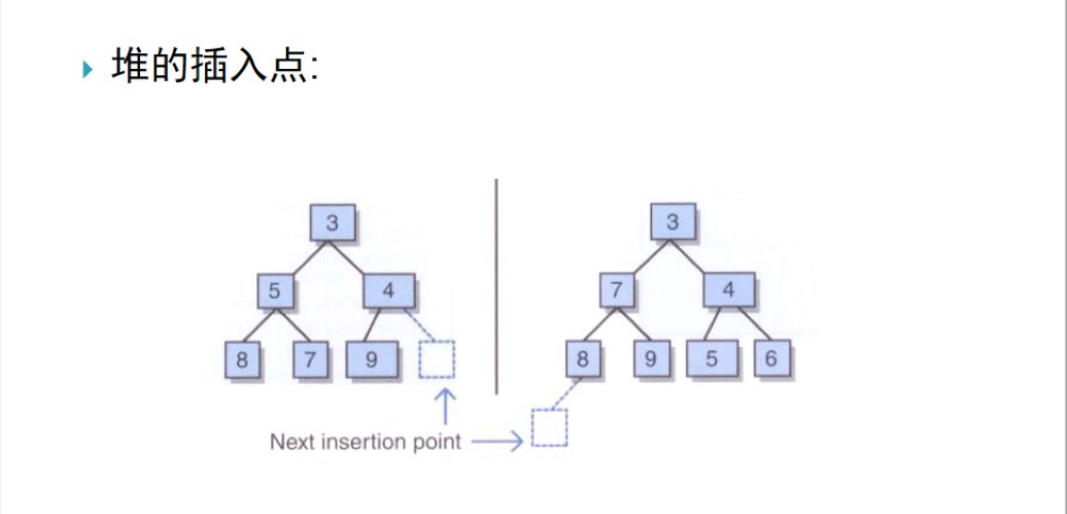
當新結點插入到正確位置之後,就要考慮到排序屬性(即將堆調整為大頂堆或小頂堆)
當調整的型別是小頂堆時,做法如下(下圖為調整過程):
只需將該新值和其雙親值進行比較,如果該新結點小於其雙親則將它們互換,我們沿著樹向上繼續這一過程,直至該新值要麼是大於其雙親要麼是位於該堆的根處
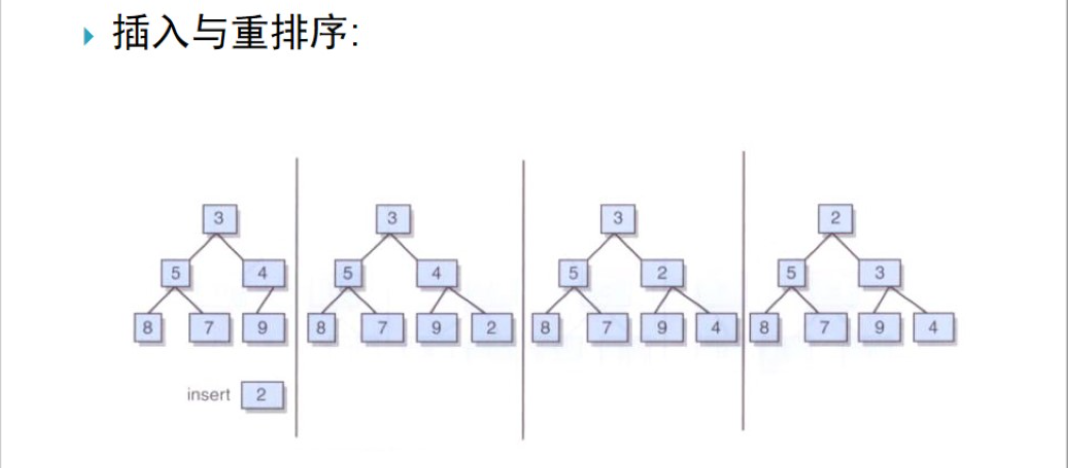
通常,在堆實現中,會對樹中的最末一片葉子進行跟蹤記錄
- removeMin操作
- removeMin方法將刪除最小堆中的最小元素並返回它
- 最小元素是儲存在最小堆的根處的,所以我們需要返回儲存在根處的元素並用堆中的另一元素替換它
- 與addElement操作一樣,是要維持該樹的完全性,那麼只有一個能替換根的合法元素,且它是儲存在樹中最末一片葉子上的元素
- 該最末一片葉子將是樹中h層上最右邊的葉子
- 替換之後,還要對堆進行調整操作,即變成最小堆(維持有序屬性)
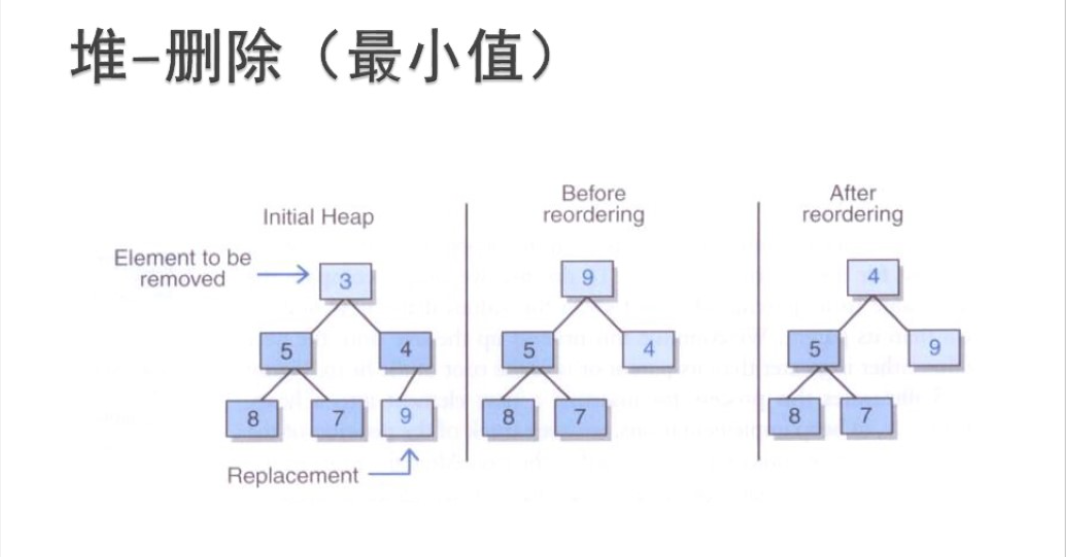
- findMin操作:返回一個指向該最小堆中最小元素的引用(該元素總是被儲存在樹根處,所以直接返回儲存在根處的元素即可)
二、使用堆:優先順序佇列
- 優先順序佇列就是遵循兩個排序規則的集合:
第一,具有更高優先順序的專案在先
第二,具有相同優先順序的專案使用先進先出方法來確定其排序 - 優先順序佇列具有多種應用(比如,作業系統中的任務排程,網路中的通訊排程,甚至是汽車維修處的作業排程)
- 可以使用某一佇列列表(其中每一佇列都表示了給定優先順序的專案)來實現一個優先順序佇列
- (這一問題的另一解決方案是使用一個最小堆)
按照優先順序對堆排序完成了第一次排序(高優先順序的專案在先)。但是,我們必須對具有相同優先順序專案的先進先出排序進行操縱:
解決方案是建立一個 PriorityQueueNode物件,它儲存的是將被放置在佇列中的元素,該元素的優先順序,以及元素放進佇列的順序
然後,我們只需為 PriorityNode類定義個 compareTo方法,以便先對優先順序進行比較,然後在優先順序一樣的時候再對階進行比較
三、用連結串列實現堆
- 堆的連結串列實現要求在插入元素後能夠向上遍歷該樹,所以堆中的結點必須儲存指向其雙親的指標
- BinaryTreeNode類沒有雙親指標,所以建立一個HeapNode類連結串列實現(對BinaryTreeNode進行擴充套件並新增一個雙親指標)
- addElement操作
addElement必須完成三個任務:
* 在恰當位置處新增一個新元素
* 對堆進行重排序以維持其排序屬性
* 將lastNode指標重新設定為指向新的最末結點- removeMin操作
removeMin方法必須完成三個任務:
* 用儲存在最末結點處的元素替換儲存在根處的元素
* 對堆進行重排序(如有必要)
* 返回初始的根元素連結串列實現的removeMin方法必須刪除根元素,並用來自最末結點的元素替換它
- findMin操作
findMin方法僅僅返回一個指向儲存在堆根處元素的引用(因此複雜度O(1) )
四、用陣列實現堆
優點:
堆的陣列實現提供了一種比連結串列實現更為簡潔的選擇。
在連結串列實現中,我們需要上下將歷樹以確定樹的最末一片葉子或下一個插入結點的雙親(連結串列實現中的許多複雜問題都與此有關)
這些困難在陣列實現中就不存在了,因為通過檢視儲存在陣列中的最末一個元素,我們就能夠確定出該樹中的最末結點與連結串列實現堆的不同之處:
樹的根位於位置0,對於每一結點n,n的左孩子將位於陣列的2n+1位置處,n的右孩子將位於陣列的2(n+1)位置處(反過來同樣也是對的)
對於任何除了根之外的結點n,n的雙親位於(n-1)/2位置處,因為我們能夠計算雙親和孩子的位置,所以與連結串列實現不同的是,陣列實現不需要建立一個 Heap Node類- addElement操作
陣列實現的addElement方法必須完成3項任務:
在恰當位置處新增新結點
對堆進行重排序以維持其排序屬性
將count遞增1跟陣列實現一樣,該方法必須首先檢查空間的可用,需要時要進行擴容
陣列實現的addElement操作與連結串列的相同(都為O(logn)),但陣列實現的效率更高
- removeMin操作
removeMin方法必須完成三項任務:
用儲存在最末元素處的元素替換儲存在根處的元素
必要時對堆進行重排序
返回初始的根元素連結串列實現和陣列實現的removeMin操作的複雜度都為O(logn)
- findMin操作
與連結串列實現的一樣,findMin方法僅僅是返回一個引用,該引用指向儲存在堆的根處或陣列的0位置處的元素,其複雜度為O(1)
五、使用堆:堆排序
使用堆來對某個數字列表進行排序:
將列表的每一元素新增到堆中,然後次一個地將它們從根中刪除,
在最小堆的情形下,排序結果將是該列表以升序排列;
在最大堆的情形下,排序結果將是該列表以降序排列堆排序的複雜度分析:
由於新增和刪除操作的複雜度都為O(log n),因此可以得出堆排序的複雜度也是O(log n),但是,這些操作的複雜度為O(log n)指的是在含有n個元素的列表中新增和刪除一個元素。
對任一給定的結點,插入到堆的複雜度都是O(log n),因此n個結點的複雜度將是 O(n log n),
刪除一個結點的複雜度為O(log n),因此對n個結點的複雜度為 O(n log n)
對於堆的排序演算法,我們需要執行addElement和 removeElement兩個操作n次,即列表中每個元素一次。因此,最終的複雜度為2 x n x logn,即 O(n log n)
教材學習中的問題和解決過程
問題1:陣列實現的addElement操作與連結串列的相同(都為O(logn)),但陣列實現的效率更高
問題1解析:
首先,先從陣列和連結串列本身來看:
一個常見的程式設計問題: 遍歷同樣大小的陣列和連結串列, 哪個比較快?
如果按照教科書上的演算法分析方法,你會得出結論,這2者一樣快, 因為時間複雜度都是 O(n)
但是在實踐中, 這2者卻有極大的差異:
通過下面的分析你會發現, 其實陣列比連結串列要快很多
首先介紹一個概念:memory hierarchy (儲存層次結構),電腦中存在多種不同的儲存器,如下表

各級別的儲存器速度差異非常大,CPU暫存器速度是記憶體速度的100倍! 這就是為什麼CPU產商發明了CPU快取。 而這個CPU快取,就是陣列和連結串列的區別的關鍵所在。
CPU快取會把一片連續的記憶體空間讀入, 因為陣列結構是連續的記憶體地址,所以陣列全部或者部分元素被連續存在CPU快取裡面, 平均讀取每個元素的時間只要3個CPU時鐘週期。
而連結串列的節點是分散在堆空間裡面的,這時候CPU快取幫不上忙,只能是去讀取記憶體,平均讀取時間需要100個CPU時鐘週期。
這樣算下來,陣列訪問的速度比連結串列快33倍!這裡只是介紹概念,具體的數字因CPU而異)
【參考資料】
從cpu和記憶體來理解為什麼陣列比連結串列查詢快
問題2:用堆來實現優先順序佇列的程式碼分析,書上只簡單介紹了,沒有具體說說程式碼的實現,簡單分析一下
問題2解析:
- 優先順序佇列是在佇列的基礎上增加限制的,所以在理解了優先順序佇列的程式碼後,PP12.1就很好做了
- 課本通過兩個類完成了堆實現的優先順序佇列
第一個PrioritizedObject類:
PrioritizedObject物件表示優先佇列中的一個節點,包含一個可比較的物件、到達順序和優先順序值
程式碼如下:
public T getElement()
{
return element;//返回節點值
}
public int getPriority()
{
return priority;//返回節點優先順序
}
public int getArrivalOrder()
{
return arrivalOrder;//返回到節點的距離順序
}
PrioritizedObject最重要的方法是優先順序的比較:
程式碼如下:
public int compareTo(PrioritizedObject obj) //如果此物件的優先順序高於給定物件,則返回1,否則返回-1
{
int result;
if (priority > obj.getPriority())
result = 1;
else if (priority < obj.getPriority())
result = -1;
else if (arrivalOrder > obj.getArrivalOrder())
result = 1;
else
result = -1;
return result;
}先比較元素的優先順序,高的先輸出;
如果優先順序一樣,再根據先進先出的方式把距離節點近的先輸出
---------------------------------------------------------------------------------------------------------------------------------
第二個就是PriorityQueue類:
首先是新增操作:
public void addElement(T object, int priority)
{
PrioritizedObject<T> obj = new PrioritizedObject<T>(object, priority);
super.addElement(obj);
}宣告PrioritizedObject變數之後,即確定了新增元素及其優先順序
這裡就直接呼叫了堆的addElement方法,完成新增功能
然後是刪除操作:直接呼叫堆的刪除最小值的方法,因為最小的元素是在堆頂處的,即佇列的頭部
public T removeNext() //從優先順序佇列中刪除下一個最高優先順序元素並返回對它的引用
{
PrioritizedObject<T> obj = (PrioritizedObject<T>)super.removeMin();
return obj.getElement();
}程式碼執行中的問題及解決過程
問題1:課後程式設計PP12.1,用堆來實現佇列,剛看完課本,都是用連結串列啊,陣列啊來實現堆的,這題要用堆來實現佇列,是要用連結串列或陣列實現的堆來實現佇列?能用佇列來實現堆嗎?課本上也有堆的一個應用:實現優先順序佇列,額,優先順序佇列和佇列有什麼不一樣嗎?
問題1解決過程:
- 首先解決一下最後一個問題:優先順序佇列和佇列
課本的定義:優先順序佇列遵循兩個排序規則的集合:具有更高優先順序的專案在先,具有相同優先順序的專案使用先進先出方法來確定其排序
百度的資料:
普通的佇列是一種先進先出的資料結構,元素在佇列尾追加,而從佇列頭刪除
在優先佇列中,元素被賦予優先順序:當訪問元素時,具有最高優先順序的元素最先刪除,優先佇列具有最高階先出
感覺很奇怪,但是仔細想了一下:
佇列只要滿足隊尾加元素,隊頭刪除元素就行了,對佇列中的元素順序沒有要求,只要在下次刪除元素前,按照優先順序把元素排好就行了把
(就像醫院排隊掛號一樣:要考慮到軍人這一優先順序的存在,要先於其他人輸出)
這一題就不用考慮到優先這一條件了
然後第二個問題,能用佇列來實現堆嗎?
這個問題。。。先留在這裡。。。哈哈哈哈哈。。。我再想想現在用堆來實現佇列
正如上面教材問題裡總結的:
在明白了優先順序佇列的實現思路後,只要把其類裡的形參Priority刪掉即可,即去掉優先順序比較的這一操作
測試結果如下:

【參考資料】
百度百科
優先順序佇列和佇列有什麼區別?
本週錯題
本週無錯題
程式碼託管
結對及互評
- 部落格中值得學習的或問題:
- 侯澤洋同學的部落格排版工整,介面很美觀,並且本週還對部落格排版、字型做了調整,很用心
- 問題總結做得很全面:對課本上不懂的程式碼會做透徹的分析,即便可以直接拿過來用而不用管他的含義
- 對教材中的細小問題都能夠關注,並且主動去百度學習
- 程式碼中值得學習的或問題:
- 對於程式設計的編寫總能找到角度去解決
- 本週結對學習情況
- 20172302
- 結對學習內容
- 第十二章內容:優先佇列與堆
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一週 | 0/0 | 1/1 | 4/4 | |
| 第二週 | 560/560 | 1/2 | 6/10 | |
| 第三週 | 415/975 | 1/3 | 6/16 | |
| 第四周 | 1055/2030 | 1/4 | 14/30 | |
| 第五週 | 1051/3083 | 1/5 | 8/38 | |
| 第六週 | 785/3868 | 1/6 | 16/54 | |
| 第七週 | 733/4601 | 1/7 | 20/74 | |
| 第八週 | 2108/6709 | 1/8 | 20/74 |
