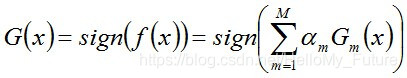1.Adaboost的原理

Adaboost是一種迭代演算法，針對同一個訓練集中的不同分類器，然後把這些弱分類器集合起來，構成一個更強的最終分類器。(Adaptive boosting)自適應增強演算法，擅長處理分類問題、標籤問題和迴歸問題，用於資料分類問題較為多見。對於分類器而言，它是基於測試過程中錯誤反饋調節的分類器的分類效果。

2.演算法的流程

演算法實際上是一個簡單的弱分類演算法的提升過程，通過不斷的訓練，從而提高資料的分類能力。具體來說，整個演算法的流程可以分為3步：

1.初始化訓練集的權值分佈，若訓練集中有N個樣本，則每個樣本的權值為 1/N;

2.在訓練的過程中，如果某個樣本被正確分類，那麼在下一輪的訓練中，這個樣本的權值就會減小，相反，若某個樣本沒有被正確分類，那麼在下一輪這個樣本的權值就會增加，所有權值變更過的樣本在下一輪中又會重新訓練，不斷的進行迭代下去。

3.最後是將各個訓練的弱分類器組合成強分類器，根據弱分類器的誤差來判斷權值，若弱分類器的誤差率較大，那麼在最終的強分類器中，它的權值就會較小，反之，誤差率較小的，那麼權值就會較大。

具體流程：

給定一個訓練資料集T={(x1,y1),(x2,y2),...(xN,yN)},其中的例項 x∈X，而例項空間X∈R，y屬於標記集合{-1,+1},

步驟1：初始化訓練資料的權值分佈，每一個初始化訓練樣本的權值為 1/N

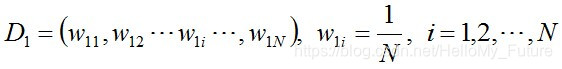
步驟2：不斷的進行迭代，用m = 1,2,...,n，來表示迭代了多少輪

使用具有權值分佈Dm的訓練資料集，得到基本分類器(一般選誤差率最低的閾值來作為基本分類器)

計算Gm(x)在資料訓練集上的分類誤差率 

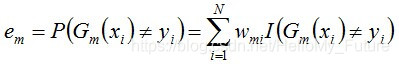
那麼，Gm(x)的分類誤差率em就是被Gm(x)誤分類樣本的權值之和。

接下來計算Gm(x)的係數，此係數am直接代表著這個分類器在最終分類器中的權重

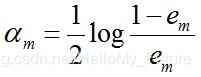
這個公式一般也可以寫成am=1/2ln( (1-em)/em),表示自然底數為e,可以得到當em ≤ 1/2時，am ≥ 0，am隨著·em的減小而增大，即誤差率越小的分類器在最終分類器中權重越大。

更新訓練集中的所有權值分佈，然後進行下一輪迭代中。

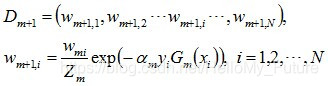
 可以得到基本分類器Gm(x)被錯誤分類的樣本權值增大，而正確分類的權值減小，比較側重於較難分的樣本上。

進行規範化，組成規範化因子Zm,使之成為一個概率分佈

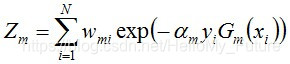
 組合各個分類器：

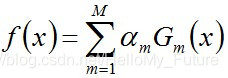
從而得到最終分類器：