資料結構

struct node{
    int val;
    node *lchild,*rchild;
};

先序非遞迴遍歷

 1)  訪問結點p，並將結點P入棧;
 2)  判斷結點P的左孩子是否為空，若為空，則取棧頂結點並進行出棧操作，
      並將棧頂結點的右孩子置為當前的結點P，迴圈->1;若不為空，則將P的左孩子置為當前的結點P;
 3) 直到P為NULL並且棧為空，則遍歷結束。

void PreOrder(node *root){
    if(!root) return ;
    node *p=root;
    stack<node *> s;
    while(p || !s.empty()){
        while(p){
            visit(p);
            s.push(p);
            p=p->lchild ; 
        }
        if(!s.empty()){
            p=s.top() ;
            s.pop() ;
            p=p->rchild;
        }
    }
}
 

中序非遞迴遍歷

1)  先掃描(並非訪問）根的所有左結點並將他們一一入棧，
2）然後出棧一個結點*p(顯然*p沒有左孩子或者左孩子結點均已經訪問)
     則訪問它，然後掃描該結點右孩子，將其入棧，再掃描右孩子的所有左結點並一一入棧，如此繼續，直至棧空 

void InOrder(node *root){
    if(!root) return;
    node *p=root;
    stack<node *> s;
    while(p || !s.empty()){ //棧不為空或p不為空
        while(p){
            s.push(p);      //根指標入棧，並遍歷左子樹
            p=p->lchild ;  
        }
        if(!s.empty()){
            p=s.top() ;    //根指標退棧，訪問根節點，遍歷右子樹
            s.pop() ;
            visit(p);
            p=p->rchild;
        }
    }
 

後續非遞迴遍歷

後續非遞迴遍歷二叉樹的順序是先變遍歷左子樹，再遍歷右子樹，最後遍歷根結點。因此一個結點被訪問的前提是無右子樹或者右子樹已經被訪問，使用輔助指標LastVisit，指向最近訪問過的結點，用pCur指向當前結點。

void PostOrder(node *root){
	if(!root) return ;
	stack<node *> s;
	node *pCur=root,*LastVisit=NULL;
	while(pCur){  //左子樹全入棧
		s.push(pCur);
		pCur=pCur->lchild ; 
	}
	while(!s.empty()){
		pCur=s.top() ;
		s.pop();
		if(pCur->lchild ==NULL || pCur->rchild ==LastVisit){ //無右子樹或根節點已被訪問
			visit(pCur);
			LastVisit=pCur;
		}
		else{
			s.push(pCur);
			pCur=pCur->rchild ;
			while(pCur){
				s.push(pCur);
				pCur=pCur->lchild ; 
			} 
		}//else
	}//while
}
 

層次遍歷

藉助佇列來實現

1）二叉樹的根節點入隊，然後出隊並訪問
     如果他有左子樹，左子樹根節點入隊，如果有右子樹，右子樹根節點入隊，然後出隊，訪問出隊結點
2）如此反覆，直至佇列為空

void BFS(node *root){
	if(!root) return ;
	node *p=root;
	queue<node *>q;
	q.push(root);
	while(!q.empty()){
		p=q.front() ;
		q.pop();
		visit(p);
		if(p->lchild!=NULL) q.push(p->lchild );
		if(p->rchild!=NULL) q.push(p->rchild );  
	} 
} 

完整程式碼：
 

#include<iostream>
#include<queue>
#include<stack>
using namespace std;

struct node{
	int val;
	node *lchild,*rchild;
};

void visit(node *root){
	cout<<root->val <<" "; 
}
 
void PreOrder(node *root){
	if(!root) return ;
	node *p=root;
	stack<node *> s;
	while(p || !s.empty()){
		while(p){
			visit(p);
			s.push(p);
			p=p->lchild ; 
		}
		if(!s.empty()){
			p=s.top() ;
			s.pop() ;
			p=p->rchild;
		}
	}
	
}

void InOrder(node *root){
	if(!root) return;
	node *p=root;
	stack<node *> s;
	while(p || !s.empty()){
		while(p){
			s.push(p);
			p=p->lchild ; 
		}
		if(!s.empty()){
			p=s.top() ;
			s.pop() ;
			visit(p);
			p=p->rchild;
		}
	}
}

void PostOrder(node *root){
	if(!root) return ;
	stack<node *> s;
	node *pCur=root,*LastVisit=NULL;
	while(pCur){
		s.push(pCur);
		pCur=pCur->lchild ; 
	}
	while(!s.empty()){
		pCur=s.top() ;
		s.pop();
		if(pCur->lchild ==NULL || pCur->rchild ==LastVisit){
			visit(pCur);
			LastVisit=pCur;
		}
		else{
			s.push(pCur);
			pCur=pCur->rchild ;
			while(pCur){
				s.push(pCur);
				pCur=pCur->lchild ; 
			} 
		}//else
	}//while
}

void BFS(node *root){
	if(!root) return ;
	node *p=root;
	queue<node *>q;
	q.push(root);
	while(!q.empty()){
		p=q.front() ;
		q.pop();
		visit(p);
		if(p->lchild!=NULL) q.push(p->lchild );
		if(p->rchild!=NULL) q.push(p->rchild );  
	} 
} 

int main(){
	node *root=new node;
	root->val=1; 
	root->lchild=new node; 
        root->rchild=new node; 
        root->lchild->val=2; 
        root->rchild->val=3;
        root->lchild->lchild=new node;
	root->lchild->rchild=new node;
	root->lchild->lchild->val =4;
	root->lchild->rchild->val =5;
	root->lchild->lchild->lchild=NULL;
	root->lchild->lchild->rchild=NULL;
	root->lchild->rchild->lchild=NULL;
	root->lchild->rchild->rchild=NULL;
	root->rchild->lchild=NULL;
	root->rchild->rchild=NULL; 
	cout<<" 先序非遞迴遍歷: " ;
	PreOrder(root);
	cout<<endl;
	cout<<" 中序非遞迴遍歷: ";
	InOrder(root);
	cout<<endl;
	cout<<" 後序非遞迴遍歷: ";
	PostOrder(root);
	cout<<endl;
	cout<<" 層次遍歷:       ";
	BFS(root);
	cout<<endl;
}

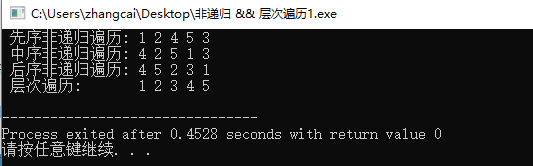
測試資料：