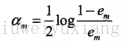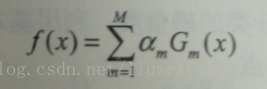整合學習(Ensemble Learning),Bagging、Boosting、Stacking
1 整合學習概述
1.1 概述
在一些資料探勘競賽中,後期我們需要對多個模型進行融合以提高效果時,常常會用Bagging,Boosting,Stacking等這幾個框架演算法,他們不是一種演算法,而是一種整合模型的框架。
整合學習在機器學習演算法中具有較高的準去率,不足之處就是模型的訓練過程可能比較複雜,效率不是很高。目前接觸較多的整合學習主要有2種:基於Boosting的和基於Bagging,前者的代表演算法有Adaboost、GBDT、XGBOOST、後者的代表演算法主要是隨機森林。
1.2 主要思想
整合學習的主要思想是利用一定的手段學習出多個分類器,而且這多個分類器要求是弱分類器,然後將多個分類器進行組合公共預測。核心思想就是如何訓練處多個弱分類器以及如何將這些弱分類器進行組合。
1.3 弱分類器選擇
一般採用弱分類器的原因在於將誤差進行均衡,因為一旦某個分類器太強了就會造成後面的結果受其影響太大,嚴重的會導致後面的分類器無法進行分類。常用的弱分類器可以採用誤差率小於0.5的,比如說邏輯迴歸、SVM、神經網路。
1.4 分類器的生成
可以採用隨機選取資料進行分類器的訓練,也可以採用不斷的調整錯誤分類的訓練資料的權重生成新的分類器。
1.5 多個弱分類區如何組合
基本分類器之間的整合方式,一般有簡單多數投票、權重投票,貝葉斯投票,基於D-S證據理論的整合,基於不同的特徵子集的整合。
下面就來分別詳細講述Bagging,Boosting,Stcking這三個框架演算法。這裡我們只做原理上的講解,不做數學上推導。
2 Bagging
2.1 基本思想
Bagging是對多個弱學習器獨立進行學習的方法。bagging方法bootstrap aggregating的縮寫。
Bootstrap是指從n個訓練樣本中隨機選取n個,允許重複,生成與原始的訓練樣本集有些許差異的樣本集的方法。
Aggregation:聚集、整合。
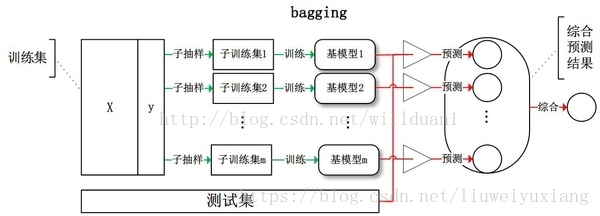
給定一個大小為n的訓練集 D,Bagging演算法從中均勻、有放回地選出 m個大小為 n’ 的子集Di,作為新的訓練集。在這 m個訓練集上使用分類、迴歸等演算法,則可得到 m個模型,再通過取平均值、取多數票等方法綜合產生預測結果,即可得到Bagging的結果。
Bagging思想的代表演算法是隨機森林,下面就以隨機森林為代表進行講解。
2.2 隨機森林演算法概述
隨機森林演算法是上世紀八十年代Breiman等人提出來的,其基本思想就是構造很多棵決策樹,形成一個森林,然後用這些決策樹共同決策輸出類別是什麼。隨機森林演算法及在構建單一決策樹的基礎上的,同時是單一決策樹演算法的延伸和改進。在整個隨機森林演算法的過程中,有兩個隨機過程,第一個就是輸入資料是隨機的從整體的訓練資料中選取一部分作為一棵決策樹的構建,而且是有放回的選取;第二個就是每棵決策樹的構建所需的特徵是從整體的特徵集隨機的選取的,這兩個隨機過程使得隨機森林很大程度上避免了過擬合現象的出現。
2.3 隨機森林演算法具體的過程:
1、從訓練資料中選取n個數據作為訓練資料輸入,一般情況下n是遠小於整體的訓練資料N的,這樣就會造成有一部分資料是無法被去到的,這部分資料稱為袋外資料,可以使用袋外資料做誤差估計。
2、選取了輸入的訓練資料的之後,需要構建決策樹,具體方法是每一個分裂結點從整體的特徵集M中選取m個特徵構建,一般情況下m遠小於M。
3、在構造每棵決策樹的過程中,按照選取最小的基尼指數進行分裂節點的選取進行決策樹的構建。決策樹的其他結點都採取相同的分裂規則進行構建,直到該節點的所有訓練樣例都屬於同一類或者達到樹的最大深度。
4、 重複第2步和第3步多次,每一次輸入資料對應一顆決策樹,這樣就得到了隨機森林,可以用來對預測資料進行決策。
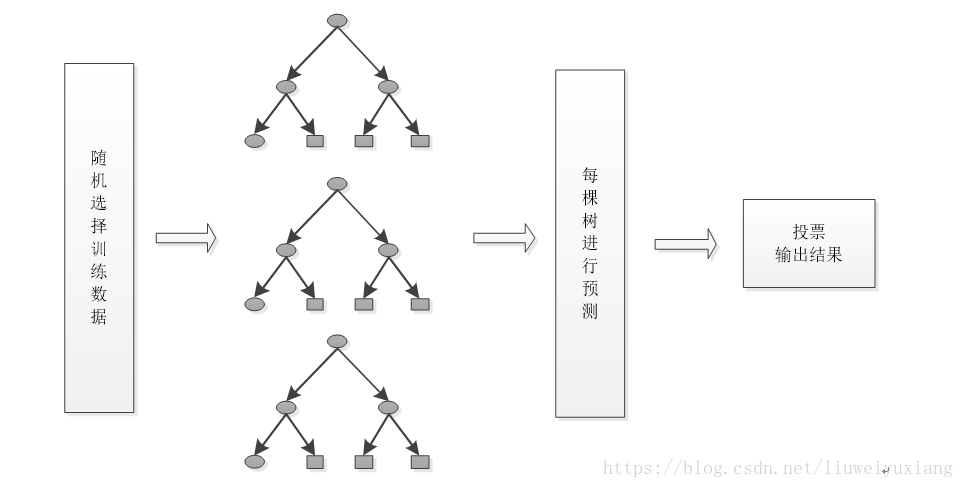
5、 輸入的訓練資料選擇好了,多棵決策樹也構建好了,對待預測資料進行預測,比如說輸入一個待預測資料,然後多棵決策樹同時進行決策,最後採用多數投票的方式進行類別的決策。
2.4 隨機森林演算法圖示
2.5 隨機森林演算法的注意點:
1、 在構建決策樹的過程中是不需要剪枝的。
2、 整個森林的樹的數量和每棵樹的特徵需要人為進行設定。
3、 構建決策樹的時候分裂節點的選擇是依據最小基尼係數的。
2.6 隨機森林有很多的優點:
a. 在資料集上表現良好,兩個隨機性的引入,使得隨機森林不容易陷入過擬合。
b. 在當前的很多資料集上,相對其他演算法有著很大的優勢,兩個隨機性的引入,使得隨機森林具有很好的抗噪聲能力。
c. 它能夠處理很高維度(feature很多)的資料,並且不用做特徵選擇,對資料集的適應能力強:既能處理離散型資料,也能處理連續型資料,資料集無需規範化。
d. 在建立隨機森林的時候,對generlization error使用的是無偏估計。
e. 訓練速度快,可以得到變數重要性排序。
f. 在訓練過程中,能夠檢測到feature間的互相影響。
g 容易做成並行化方法。
h. 實現比較簡單。
3 Boosting
Boosting是對多個弱學習器依次進行學習的方法。Boosting有很多種,比如AdaBoost(Adaptive Boosting), Gradient Boosting等,這裡以AdaBoost為典型講解一下。
Boosting也是集合了多個決策樹,但是Boosting的每棵樹是順序生成的,每一棵樹都依賴於前一顆樹。順序執行會導致執行速度慢。
3.1 AdaBoosting基本思想
首先介紹下AdaBoost的思想,而不去闡述Boosting決策樹的構建構建方法和數學公式推導。
AdaBoost,運用了迭代的思想。每一輪都加入一個新訓練一個預測函式,直到達到一個設定的足夠小的誤差率,或者達到最大的樹的數目。
①開始的時候每一個訓練樣本都被賦予一個初始權重,用所有樣本訓練第一個預測函式。計算該預測函式的誤差,然後利用該誤差計算訓練的預測函式的權重係數(該預測函式在最終的預測函式中的權重,此處忽略公式)。接著利用誤差更新樣本權重(此處忽略公式)。如果樣本被錯誤預測,權重會增加;如果樣本被正確預測,權重會減少。通過權重的變化,使下輪的訓練器對錯誤樣本的判斷效果更好。
②以後每輪訓練一個預測函式。根據最後得出的預測函式的誤差計算新訓練的預測函式在最終預測中的權重,然後更新樣本的權重。權重更新之後,所有樣本用於下輪的訓練。
③如此迭代,直到誤差小於某個值或者達到最大樹數。
這裡涉及到兩個權重,每輪新訓練的預測函式在最終預測函式中所佔的權重和樣本下一輪訓練中的權重。這兩個權重都是關於 每輪訓練的預測函式產生的誤差 的函式。
3.2 Adaboost的演算法流程:
假設訓練資料集為T={(X1,Y1),(X2,Y2),(X3,Y3),(X4,Y4),(X5,Y5)} 其中Yi={-1,1}
1、初始化訓練資料的分佈
訓練資料的權重分佈為D={W11,W12,W13,W14,W15},其中W1i=1/N。即平均分配。
2、選擇基本分類器
這裡選擇最簡單的線性分類器y=aX+b ,分類器選定之後,最小化分類誤差可以求得引數。
3、計算分類器的係數和更新資料權重
誤差率也可以求出來為e1.同時可以求出這個分類器的係數。基本的Adaboost給出的係數計算公式為
上面求出的
就是這個分類器在最終的分類器中的權重。然後更新訓練資料的權重分佈。如果樣本被錯誤預測,權重會增加;如果樣本被正確預測,權重會減少。
總而言之:Boosting每次迭代迴圈都是利用所有的訓練樣本,每次迭代都會訓練出一個分類器,根據這個分類器的誤差率計算出該分類器的在最終的分類器中的權重,並且更新訓練樣本的權重。這就使得每次迭代訓練出的分類器都依賴上一次的分類器,序列速度慢。
3.3 Boosting最終的組合弱分類器方式:
通過加法模型將弱分類器進行線性組合,比如AdaBoost通過加權多數表決的方式,即增大錯誤率小的分類器的權值,同時減小錯誤率較大的分類器的權值。
4 Stacking
以Adaboost為代表的Boosting和以RandomForest為代表的Bagging,它們在整合學習中屬於同源整合(homogenous ensembles)方法。Stacking 也就是Stacked Generalization(SG),翻譯為堆疊泛化的方法(屬於異源整合(heterogenous ensembles)的典型代表)。
4.1 堆疊泛化(Stacked Generalization)的概念
作為一個在kaggle比賽中高分選手常用的技術,SG在部分情況下,甚至可以讓錯誤率相比當前最好的方法進一步降低30%之多。
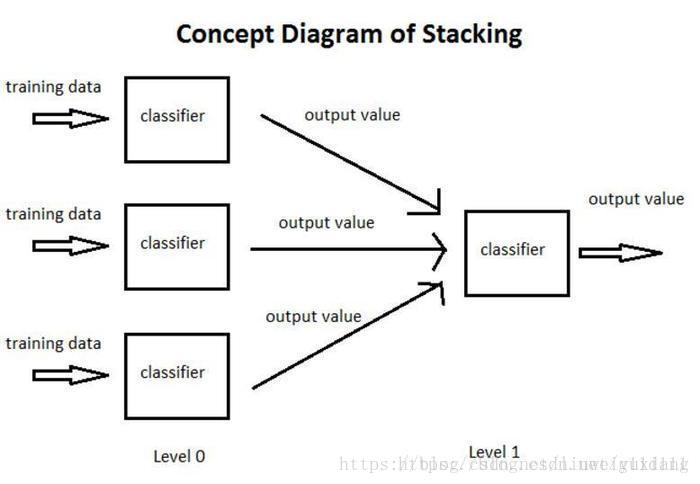
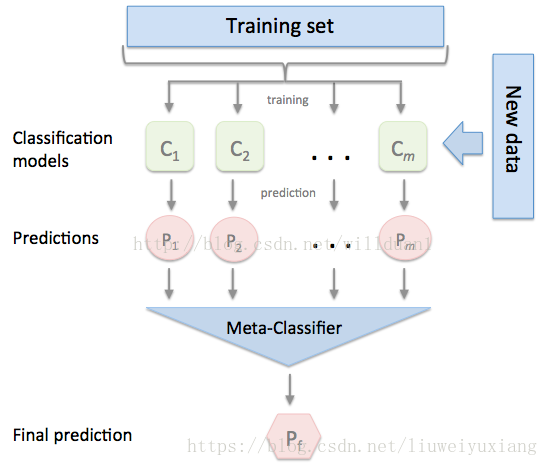
以下圖為例,簡單介紹一個什麼是SG:
① 將訓練集分為3部分,分別用於讓3個基分類器(Base-leaner)進行學習和擬合
② 將3個基分類器預測得到的結果作為下一層分類器(Meta-learner)的輸入
③ 將下一層分類器得到的結果作為最終的預測結果
這個模型的特點就是通過使用第一階段(level 0)的預測作為下一層預測的特徵,比起相互獨立的預測模型能夠有**更強的非線性表述能力,降低泛化誤差。**它的目標是同時降低機器學習模型的Bias-Variance。
總而言之,堆疊泛化就是整合學習(Ensemble learning)中Aggregation方法進一步泛化的結果, 是通過Meta-Learner來取代Bagging和Boosting的Voting/Averaging來綜合降低Bias和Variance的方法。 譬如: Voting可以通過kNN來實現, weighted voting可以通過softmax(Logistic Regression), 而Averaging可以通過線性迴歸來實現。
4.2 Stacking 整合思想
將訓練好的所有基模型對整個訓練集進行預測,第j個基模型對第i個訓練樣本的預測值將作為新的訓練集中第i個樣本的第j個特徵值,最後基於新的訓練集進行訓練。同理,預測的過程也要先經過所有基模型的預測形成新的測試集,最後再對測試集進行預測:
4.3 mlxtend庫的Stacking 三種整合方式實現
下面我們介紹一款功能強大的stacking利器,mlxtend庫,它可以很快地完成對sklearn模型地stacking。
主要有以下幾種使用方法吧:
I. 最基本的使用方法,即使用前面分類器產生的特徵輸出作為最後總的meta-classifier的輸入資料
from sklearn import datasets
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
import numpy as np
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
meta_classifier=lr)
print('3-fold cross validation:\n')
for clf, label in zip([clf1, clf2, clf3, sclf],
['KNN',
'Random Forest',
'Naive Bayes',
'StackingClassifier']):
scores = model_selection.cross_val_score(clf, X, y,
cv=3, scoring='accuracy')
print("Accuracy: %0.2f (+/- %0.2f) [%s]"
% (scores.mean(), scores.std(), label))
II. 另一種使用第一層基本分類器產生的類別概率值作為meta-classfier的輸入
這種情況下需要將StackingClassifier的引數設定為 use_probas=True。如果將引數設定為 average_probas=True,那麼這些基分類器對每一個類別產生的概率值會被平均,否則會拼接。
例如有兩個基分類器產生的概率輸出為:
classifier 1: [0.2, 0.5, 0.3]
classifier 2: [0.3, 0.4, 0.4]
1) average = True :
產生的meta-feature 為:[0.25, 0.45, 0.35]
2) average = False:
產生的meta-feature為:[0.2, 0.5, 0.3, 0.3, 0.4, 0.4]
from sklearn import datasets
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingClassifier
import numpy as np
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3],
use_probas=True,
average_probas=False,
meta_classifier=lr)
print('3-fold cross validation:\n')
for clf, label in zip([clf1, clf2, clf3, sclf],
['KNN',
'Random Forest',
'Naive Bayes',
'StackingClassifier']):
scores = model_selection.cross_val_score(clf, X, y,
cv=3, scoring='accuracy')
print("Accuracy: %0.2f (+/- %0.2f) [%s]"
% (scores.mean(), scores.std(), label))
III. 另外一種方法是對訓練基中的特徵維度進行操作的
這次不是給每一個基分類器全部的特徵,而是給不同的基分類器分不同的特徵,即比如基分類器1訓練前半部分特徵,基分類器2訓練後半部分特徵(可以通過sklearn 的pipelines 實現)。最終通過StackingClassifier組合起來。
from sklearn.datasets import load_iris
from mlxtend.classifier import StackingClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
iris = load_iris()
X = iris.data
y = iris.target
pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)),
LogisticRegression())
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)),
LogisticRegression())
sclf = StackingClassifier(classifiers=[pipe1, pipe2],
meta_classifier=LogisticRegression())
sclf.fit(X, y)
4.4 StackingClassifier 使用API及引數解析:
StackingClassifier(classifiers, meta_classifier, use_probas=False, average_probas=False, verbose=0, use_features_in_secondary=False)
引數:
classifiers : 基分類器,陣列形式,[cl1, cl2, cl3]. 每個基分類器的屬性被儲存在類屬性 self.clfs_.
meta_classifier : 目標分類器,即將前面分類器合起來的分類器
use_probas : bool (default: False) ,如果設定為True, 那麼目標分類器的輸入就是前面分類輸出的類別概率值而不是類別標籤
average_probas : bool (default: False),用來設定上一個引數當使用概率值輸出的時候是否使用平均值。
verbose : int, optional (default=0)。用來控制使用過程中的日誌輸出,當 verbose = 0時,什麼也不輸出, verbose = 1,輸出迴歸器的序號和名字。verbose = 2,輸出詳細的引數資訊。verbose > 2, 自動將verbose設定為小於2的,verbose -2.
use_features_in_secondary : bool (default: False). 如果設定為True,那麼最終的目標分類器就被基分類器產生的資料和最初的資料集同時訓練。如果設定為False,最終的分類器只會使用基分類器產生的資料訓練。
屬性:
clfs_ : 每個基分類器的屬性,list, shape 為 [n_classifiers]。
meta_clf_ : 最終目標分類器的屬性
方法:
fit(X, y)
fit_transform(X, y=None, fit_params)
get_params(deep=True),如果是使用sklearn的GridSearch方法,那麼返回分類器的各項引數。
predict(X)
predict_proba(X)
score(X, y, sample_weight=None), 對於給定資料集和給定label,返回評價accuracy
set_params(params),設定分類器的引數,params的設定方法和sklearn的格式一樣
5 一個例子說明整合學習為什麼可以提高準確率
上面提到了同源整合經典方法中的Voting和Averaging,這裡以分類任務為例,對Voting進行說明,那麼什麼是Voting呢?
Voting,顧名思義,就是投票的意思,假設我們的測試集有10個樣本,正確的情況應該都是1:
我們有3個正確率為70%的二分類器記為A,B,C。你可以將這些分類器視為偽隨機數產生器,即以70%的概率產生”1”,30%的概率產生”0”。
下面我們可以根據從眾原理(少數服從多數),來解釋採用整合學習的方法是如何讓正確率從70%提高到將近79%的。
All three are correct 0.7 * 0.7 * 0.7 = 0.3429
Two are correct 0.7 * 0.7 * 0.3 + 0.7 * 0.3 * 0.7 + 0.3 * 0.7 * 0.7 = 0.4409
Two are wrong 0.3 * 0.3 * 0.7 + 0.3 * 0.7 * 0.3 + 0.7 * 0.3 * 0.3 = 0.189
All three are wrong 0.3 * 0.3 * 0.3 = 0.027
我們看到,除了都預測為正的34,29%外,還有44.09%的概率(2正1負,根據上面的原則,認為結果為正)認為結果為正。大部分投票整合會使最終的準確率變成78%左右(0.3429 + 0.4409 = 0.7838)。
注意,這裡面的每個基分類器的權值都認為是一樣的。