整合學習概述(Bagging,RF,GBDT,Adaboost)
博主在之前的部落格當中介紹過利用決策樹處理迴歸和分類的問題(基於CART的迴歸和分類任務),決策樹解釋性好但是模型方差較大,且容易過擬合。在本篇部落格中,博主打算對常用的整合學習進行介紹,主要注重模型的思想和解決的問題。
1 整合學習概述
1.1 主流演算法
整合學習(Ensemble Learning) 在機器學習演算法中具有較高的準去率,不足之處就是模型的訓練過程可能比較複雜,效率不是很高。目前整合學習主要有2種:基於 Boosting 的和基於 Bagging,前者的代表演算法有 Adaboost、GBDT、XGBOOST 等、後者的代表演算法主要是隨機森林(Random Forest)
1.2 主要思想
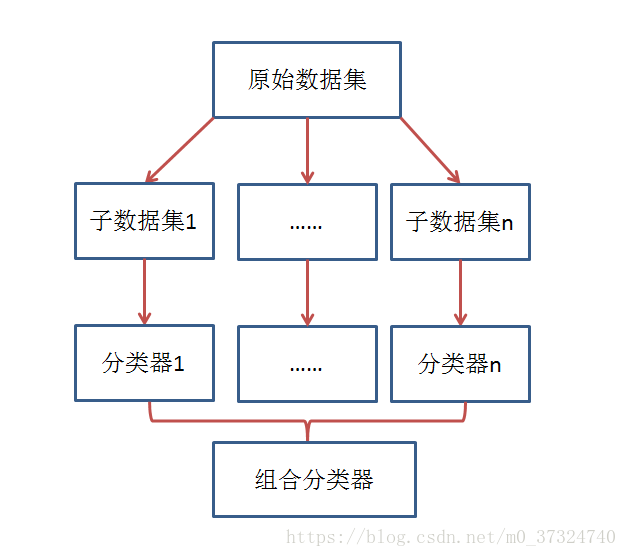
整合學習的主要思想訓練多個弱分類器,然後將多個分類器進行組合預測。核心思想就是如何訓練處多個弱分類器以及如何將這些弱分類器進行組合。實現的思路如下圖所示:
組合分類器效能通常是優於單個分類器的,但是需要滿足兩個條件:
- 基分類器之間應該相互獨立(至少相關性不高)
- 基分類器應該好於隨機猜測分類器(在二分類中應該高於0.5的準確率)
但是基分類器是為了解決同一個問題而訓練出來的,顯然彼此間很難獨立,因此根據基分類器的生成方式整合學習又可以分為兩大類:
- 基分類器之間有較強的依賴關係,序列生成序列,如 Boosting
- 基分類器之間的依賴關係不強,並行生成序列,如 Bagging
2 各類演算法
2.1 Bagging 演算法
Bagging(裝袋)又稱為自助聚集(bootstrap aggregating),它得到不同資料集的方式是均勻的概率從訓練集中重複的抽樣,一般來說自助樣本的包含設63%的原始訓練資料。
Bagging 通過降低基分類器的方差改善了泛化誤差。
需要注意的是,如果基分類器實不穩定的,bagging有助於減少訓練資料的隨機波動導致的誤差,如果基分類器實問題定的,即對訓練資料集中的微小變化是魯棒的,則組合分類器的誤差主要有基分類器偏移所引起的,這種情況下,bagging可能不會對基分類器有明顯的改進效果,甚至可能降低分類器的效能。
2.1.1 Random Forest
隨機森林是 Bagging 的擴充套件,實質是專門為決策樹分類器設計的一種組合方法,在分類問題中採用投票表決;在迴歸問題中採用的是取平均值。隨機森林有兩個隨機過程:
- 隨機有放回的取樣,和 Bagging 一樣
- 隨機從 m 個特徵中選擇 n 個特徵用於決策樹的訓練 (通常 n=
)
隨機森林相比於決策樹沒有剪枝的過程,然而正因為兩個隨機的過程,對樹的操作實現了去相關。其效能要高於決策樹。
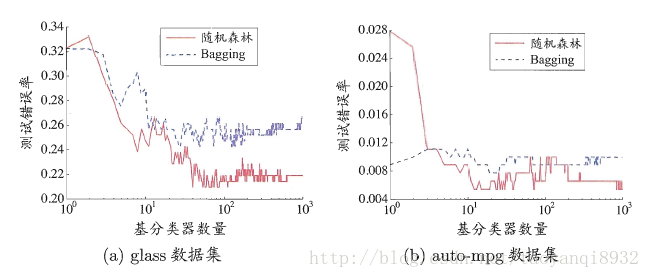
在基分類器較少的時候效能可能不如 Bagging 方法(畢竟隨機森林加入了特徵干擾), 然而隨著樹的增加,其效果會好於 Bagging,如下圖:
2.2 boosting 演算法
Gradient Boosting(梯度提升)是一種整合弱學習模型的機器學習方法。又叫 MART(Multiple Additive Regression Tree),是一種迭代的決策樹演算法,該演算法由多棵決策樹(確切的說是迴歸樹)組成,所有樹的結論累加起來做最終答案。
2.2.1 GBDT (Gradient Boosting Decision Tree)
GBDT,又叫 MART(Multiple Additive Regression Tree),是一種迭代的決策樹演算法,該演算法由多棵決策樹(確切的說是迴歸樹)組成,所有樹的結論累加起來做最終答案。GBDT的核心就在於,每一棵樹學的是之前所有樹結論和的殘差,這個殘差就是一個加預測值後能得真實值的累加量。
下面用個簡單的例子說明。
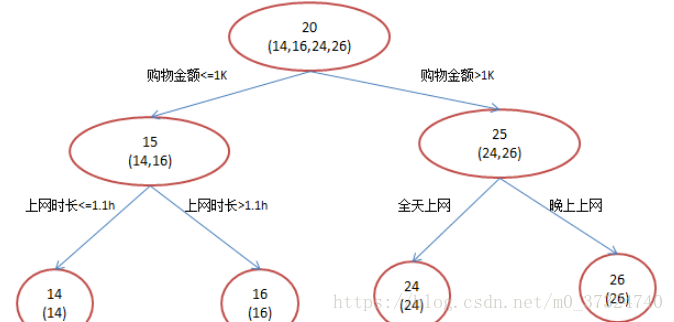
訓練集是4個人,A,B,C,D年齡分別是14,16,24,26。樣本中有購物金額、上網時長、經常到百度知道提問等特徵。現在用決策樹模型和 GBDT模型。
- 決策樹模型
訓練過程如下圖:
- GBDT 模型
訓練過程如下圖:

A: 14歲高一學生,購物較少,經常問學長問題;預測年齡A = 15 – 1 = 14
B: 16歲高三學生;購物較少,經常被學弟問問題;預測年齡B = 15 + 1 = 16
C: 24歲應屆畢業生;購物較多,經常問師兄問題;預測年齡C = 25 – 1 = 24
D: 26歲工作兩年員工;購物較多,經常被師弟問問題;預測年齡D = 25 + 1 = 26
看到這裡,你可能會有下面的問題:
- 哪裡體現梯度?
以誤差作為衡量標準,殘差向量(-1, 1, -1, 1)都是它的全域性最優方向,這就是Gradient。
- 既然最後的結果是一樣的,為什麼用 GBDT模型?
為了防止過擬合。決策樹模型為了達到100%精度使用了3個feature(上網時長、時段、網購金額),其中分枝“上網時長>1.1h” 很顯然已經過擬合了,這個資料集上A,B也許恰好A每天上網1.09h, B上網1.05小時,但用上網時間是不是>1.1小時來判斷所有人的年齡很顯然是有悖常識的。
- 既然用殘差作為負梯度是一個特例,那麼通用的演算法步驟是如何的?
首先進行如下說明,當損失函式時平方損失和指數損失函式時,每一步的優化很簡單,如平方損失函式學習殘差迴歸樹。

但對於一般的損失函式,往往每一步優化沒那麼容易,如上圖中的絕對值損失函式和Huber損失函式。針對這一問題,Freidman提出了梯度提升演算法:利用最速下降的近似方法,即利用損失函式的負梯度在當前模型的值,作為迴歸問題中提升樹演算法的殘差的近似值,擬合一個迴歸樹。
具體演算法遵循以下的步驟:
1、初始化,估計使損失函式極小化的常數值,它是隻有一個根節點的樹,即ganma是一個常數值。
2、重複以下步驟:
(a)計算損失函式的負梯度在當前模型的值,將它作為殘差的估計
(b)估計迴歸樹葉節點區域,以擬合殘差的近似值
(c)利用線性搜尋估計葉節點區域的值,使損失函式極小化
(d)更新迴歸樹
3、得到輸出的最終模型 f(x)
2.2.2 Adaboost(Adaptive boosting )
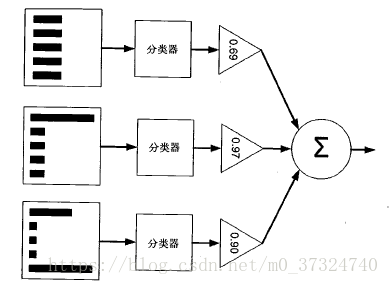
Adaboost是一種迭代演算法,其核心思想是針對同一個訓練集訓練不同的分類器(弱分類器),然後把這些弱分類器集合起來,構成一個更強的最終分類器(強分類器)。其原理如下圖:
Adaboost 演算法示意圖(左邊的是資料集,直方圖的不同寬度表示每個樣例上的不同權重
在經過一個分類器之後,加權的預測結果會通過三角形中的數值進行加權,在後一步的
圓形框中求和,得到最後的結果)
演算法過程遵循以下的步驟(主要在於每個分類器中樣本權重的更新和每個分類器中樣本權重的更新):
- 對於每個分類器,賦予分類器中樣本 i 的權重為 Di (初始權重等值)
- 第一次在訓練的時候得到每個分類器的分類錯誤率:
- 第二次訓練的時候,更新每個分類器的權重α,
,更新每個分類器中樣本的權重Di(如果樣本正確分類,則樣本的權重更新為:
;如果樣本錯誤分類,則樣本的權重更新為:
),正確分裂的樣本權重降低,錯誤分類的樣本權重增大
- 重複步驟3,直到分類器的錯誤率為0或者達到設定值
3 各自特點
Bagging 模型降低方差, Boosting 模型降低偏差。
事實上,就機器學習演算法來說,其泛化誤差可以分解為兩部分,偏差(bias)和方差(variance),如下公式:
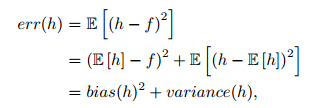
偏差指的是演算法的期望預測與真實預測之間的偏差程度,反應了模型本身的擬合能力;方差度量了同等大小的訓練集的變動導致學習效能的變化,刻畫了資料擾動所導致的影響。
當模型越複雜時,擬合的程度就越高,模型的訓練偏差就越小。但此時如果換一組資料可能模型的變化就會很大,即模型的方差很大。所以模型過於複雜的時候會導致過擬合。當模型越簡單時,即使我們再換一組資料,最後得出的學習器和之前的學習器的差別就不那麼大,模型的方差很小。還是因為模型簡單,所以偏差會很大,如下圖:

對於Bagging演算法來說,由於我們會並行地訓練很多不同的分類器的目的就是降低這個方差(variance) ,因為採用了相互獨立的基分類器多了以後,h的值自然就會靠近
。所以對於每個基分類器來說,目標就是如何降低這個偏差(bias),所以我們會採用深度很深甚至不剪枝的決策樹(隨機森林模型不需要剪枝)。
對於Boosting來說,每一步我們都會在上一輪的基礎上更加擬合原資料,所以可以保證偏差(bias),所以對於每個基分類器來說,問題就在於如何選擇variance更小的分類器,即更簡單的分類器,所以我們選擇了深度很淺的決策樹。
參考資料:
https://www.jianshu.com/p/005a4e6ac775
https://www.zhihu.com/question/45487317/answer/99153174
《統計學習導論——基於R的應用》
《機器學習實戰 》
《機器學習》周志華