2018-10-18 08:38:17

---

 

原題連結：

P2449 [SDOI2005]矩形

題目描述

現在我們在一個平面上畫了n個矩形。每一個矩形的兩邊都與座標軸相平行，且矩形定點的座標均為整數。

現我們定義滿足如下性質的圖形為一個塊：

1.每一個矩形都是一個塊；

2.如果兩個塊有一段公共的部分，那麼這兩個塊就會形成一個新的塊，否則這兩個塊就是不同的。

示例：

圖1中的矩形形成了兩個不同的塊。圖2中的矩形形成了一個塊。

任務：

請寫一個程式：

1.從文字檔案PRO.IN中讀入各個矩形的頂點座標；

2.找出這些矩形中不同的塊的數目；

3.把結果輸出到文字檔案PRO.OUT中。

輸入輸出格式

輸入格式：

 

文字檔案PRO.IN的第一行包括一個整數n，1<=n<=7000，為矩形的數目。以下的n行為矩形頂點的座標。

每一個矩形都是用四個整數來描述的：左下角的x座標、左下角的y座標、右上角的x座標和右上角的y座標。

所有的座標都是不大於10000的非負整數。

 

輸出格式：

 

在文字檔案PRO.OUT中輸出唯一的一個整數——這些矩形所形成的不同的塊的數目。

 

輸入輸出樣例

輸入樣例#1： 

9
0 3 2 6
4 5 5 7
4 2 6 4
2 0 3 2
5 3 6 4
3 2 5 3
1 4 4 7
0 0 1 4
0 0 4 1

輸出樣例#1：

2

---

♦題目大意：
輸入n個矩形，若兩個矩形重合則將這兩個矩形合併在一起，最後問一共有幾塊區域？
注意：兩個矩形邊與邊重合能合成一塊，而兩個矩形點與點重合則不行！
 

♦思路：
顯然，一個並查集不就搞定了嗎？
可是！這道題的難點並不是並查集本身吧，更多的是怎麼判斷這兩個矩形重合！
一開始，我的思路是將a矩形內的點全部標記一下，再列舉b矩形，看b矩形中有a矩形標記
過的幾個點，若點大於1，則表示重合。雖然，這個方法是可行的，但是看資料範圍，矩形
的座標是不大於10000的非負整數，啊，顯然就炸掉了！那怎麼辦呢？我我又很懶，那懶人
有懶方法，嗯，就從反向考慮吧！
如果b矩形的4個點的橫座標都大於a矩形的下點橫座標/都小於a矩形的上點橫座標..（依
舊很懶，如圖，紅色為a矩形，綠色為b矩形）

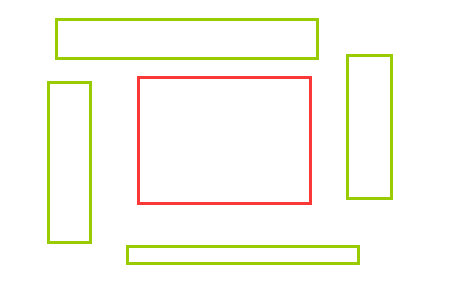
這4種情況則是不重合，那麼怎麼判斷只有一個點重合的情況呢？其實只要特判一下就好了！

這樣，這道題就AC了！

---

#include<bits/stdc++.h>
using namespace std;

int n;
struct Squ{int x,y,xx,yy;}squ[7000+10];
int fa[7000+10]; 
int ans[7000+10],oo;
int fi,fj;
int c;

int jud(int d,int dd)
  {
     int xf1=squ[d].x,yf1=squ[d].y,xf2=squ[d].xx,yf2=squ[d].yy;
     int xl1=squ[dd].x,yl1=squ[dd].y,xl2=squ[dd].xx,yl2=squ[dd].yy;
     if((xl1<xf1&&xl2<xf1)||(xl1>xf2&&xl2>xf2)||(yl1<yf1&&yl2<yf1)||(yl1>yf2&&yl2>yf2)) return 0;
     if((xl1==xf2&&yl1==yf2)||(xl1==xf2&&yl2==yf1)||(xl2==xf1&&yl1==yf2)||(xl2==xf1&&yl2==yf1)) return 0;
     return 1;
  }

int find(int x)
  {
      if(fa[x]==x) return x;
      return fa[x]=find(fa[x]);
  }

int main()
  {
      scanf("%d",&n);
      for(int i=1;i<=n;i++)
        scanf("%d%d%d%d",&squ[i].x,&squ[i].y,&squ[i].xx,&squ[i].yy);
      for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=2;i<=n;i++)
        for(int j=1;j<=i-1;j++)
          {
              c=jud(j,i);
            if(c==1)
                {
                    fi=find(i);
                    fj=find(j);
                    if(fi!=fj) fa[fi]=fj;
              }
        }
    for(int i=1;i<=n;i++)
      {
          fa[i]=find(i);
        ans[fa[i]]++;
      }
    for(int i=1;i<=n;i++)
      if(ans[i]>0) oo++;
    //for(int i=1;i<=n;i++)
      //printf("%d",fa[i]);
    printf("%d",oo);
    return 0;  
  }