網路流--最大流dinic講解
這幾年聯賽總考一些出其不意的知識點。博主發現網路流能解決的東西很多,所以這兩天抽空學習了最大流dinic演算法。
看著這個冠冕堂皇的名詞,何為網路流?我先百度一下定義
https://baike.baidu.com/item/%E7%BD%91%E7%BB%9C%E6%B5%81/2987528?fr=aladdin
網路流(network-flows)是一種類比水流的解決問題方法,與線性規劃密切相關。網路流的理論和應用在不斷髮展,出現了具有增益的流、多終端流、多商品流以及網路流的分解與合成等新課題。網路流的應用已遍及通訊、運輸、電力、工程規劃、任務分派、裝置更新以及計算機輔助設計等眾多領域。
什麼鬼???
捕捉關鍵資訊,發現一個詞“水流”。把它理解在圖中,就是在一條路徑中最小的那個邊權啦!

如果源點為6,終點為7的話水流1次就變成下面這個圖。
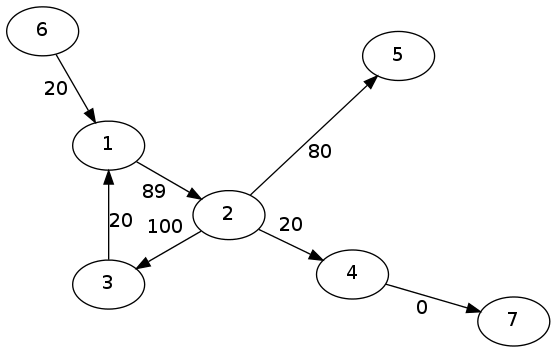
流一次6->1->2->4->7,流過10單位的水流。
但接下來原點並不能到達匯點,故最大流是10.
有的同學說:“dfs沒問題!”,別急,看下一個圖。
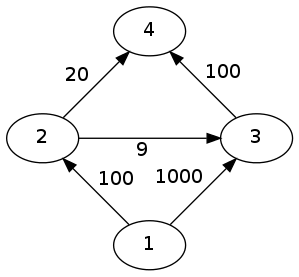
求從1到4的最大流量。
我們萬一走到了這條路徑1->2->3->4
變成這樣
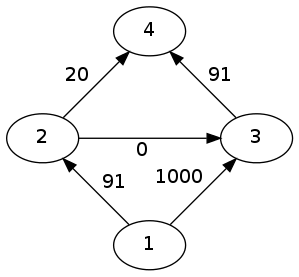
再次增廣 ......
時間要炸了,這可怎麼辦啊?
進入今天的正題 dinic
為了解決我們上面遇到的低效方法,dinic演算法引入了一個東西,叫做分層圖。就是對於每一個點,我們根據從源點開始的bfs序列,為每一個點分配一個深度,然後我們進行若干遍dfs尋找增廣路,每一次由u推出v必須保證v的深度必須是u的深度+1。
有用嗎?
當然。
根據上面的圖,從1到4
dep[1]=0,dep[2]=dep[3]=1,dep[4]=2
這樣dfs每搜一次就更新一下當前流量,但如果走錯了怎麼辦?
沒關係,連一條反向邊就OK了。
反向邊一開始的tot要製成1,這樣tot^1就能找到反向邊的編號啦!
分析時間複雜度,最壞情況下為O(n2m),但是遠遠要優於它,因為次數是單調遞減的。n<=1000的問題基本都可以解決。
另外說一下:網路流的難點是建模(真的好難),並不是實現過程。最大流BFS+DFS,費用流再用個SPFA,僅此而已。
來道USACO模版題
https://neooj.com:8082/oldoj/problem.php?id=1817
Drainage Ditches 草地排水
Description
在農夫約翰的農場上,每逢下雨,貝茜最喜歡的三葉草地就積聚了一潭水.這意味著草地被水淹沒了,並且小草要繼續生長還要花相當長一段時間.因此,農夫約翰修建了一套排水系統來使貝茜的草地免除被大水淹沒的煩惱(不用擔心,雨水會流向附近的一條小溪).作為一名一流的技師,農夫約翰
已經在每條排水溝的一端安上了控制器,這樣他可以控制流入排水溝的水流量.
農夫約翰知道每一條排水溝每分鐘可以流過的水量,和排水系統的準確佈局(起點為水潭而終點為小溪的一張網).需要注意的是,有些時候從一處到另一處不只有一條排水溝.
根據這些資訊,計算從水潭排水到小溪的最大流量.對於給出的每條排水溝,雨水只能沿著一個方向流動,注意可能會出現雨水環形流動的情形.
Input
第1 行: 兩個用空格分開的整數N (0 <= N <= 200) 和 M (2 <= M <= 200).N 是農夫約翰已經挖好的排水溝的數量,M 是排水溝交叉點的數量.交點1 是水潭,交點M 是小溪.
第二行到第N+1 行: 每行有三個整數,Si, Ei, 和 Ci.Si 和 Ei (1 <= Si, Ei <= M) 指明排水溝兩端的交點,雨水從Si 流向Ei.Ci (0 <= Ci <= 10,000,000)是這條排水溝的最大容量.
Output
輸出一個整數,即排水的最大流量.
Sample Input
5 4 1 2 40 1 4 20 2 4 20 2 3 30 3 4 10Sample Output
50 說白了就是求整個圖中的最大流。 貼程式碼了#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
#define N 1000
int n,m;
int idx=1;
int head[N];
int to[N];
int val[N];
int nex[N];
int a,b,c;
int ans;
int dep[N];
int s;
void addedge(int a,int b,int c)
{
nex[++idx]=head[a];
head[a]=idx;
to[idx]=b;
val[idx]=c;
}
bool bfs()
{
queue <int> q;
q.push(1);
memset(dep,-1,sizeof(dep));
dep[1]=0;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=head[x];i;i=nex[i])
{
if((val[i])&&dep[to[i]]==-1)
{
dep[to[i]]=dep[x]+1;
q.push(to[i]);
if(to[i]==n)
return true;
}
}
}
return false;
}
int dinic(int x,int flow)
{
int nowflow=flow;
if(x==n)
return nowflow;
for(int i=head[x];i;i=nex[i])
{
if(val[i]>0&&dep[to[i]]==dep[x]+1)
{
int now=dinic(to[i],min(val[i],nowflow));
if(now==0)
dep[to[i]]=-1;
nowflow-=now;
val[i]-=now;
val[i^1]+=now;
if(nowflow==0)
break;
}
}
return flow-nowflow;
}
int main()
{
scanf("%d%d",&m,&n);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a,&b,&c);
addedge(a,b,c);
addedge(b,a,0);
}
while(bfs())
ans+=dinic(1,1<<30);
printf("%d",ans);
}
