反向傳播演算法（Backpropagation algorithm即BP演算法）

看了好幾篇相關文章，終於大致搞清楚了反向傳播時候隱藏層的誤差求導到底是怎麼算的，，，為了防止遺忘還是記一下。

每一個神經元就像一個蘋果一樣，用net表示左一半（和它前面一層相關），out表示右一半（和後一層相關）。這兩半之間的關係，就是啟用函式作用在net上，到右邊就是out了。

用實際的例子來理解正向傳播比較清楚，反向傳播也是根據鏈式求導不斷導導導直到出來和本層輸入和輸出相關的公式。我都快暈了。。。為方便記憶用2*2*2的三層神經網路說明。

變數說明：i為輸入，h為隱藏層，o為輸出層，b為偏置（我的理解是就是加一個常數項，但是後面只更新權重，並沒去更新這個常數，不知道為啥，有待繼續學習...）

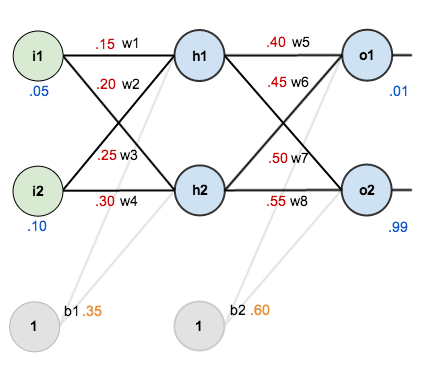
前向傳播就是按照：

比如：輸入層到隱藏層h:

,為啟用函式，這裡假設為sigmoid函式。對於不同的層，加上對應的腳註就好了。然後一直乘上各自權重再加上偏值，一直到最後一層。

主要記錄一下反向傳播求導：

有兩個輸出神經元的話，設第一個神經元輸出誤差損失為E1，第二個為E2。公式就是

一開始不知道為啥要求導，這和誤差損失有啥關係，後來看了文末的文章知道了，對誰求導就是看一下它對誤差損失帶來多大的影響。對所有權重都要求導，看看權重的影響。最後不斷更新權重，這就是誤差反向傳播的目的吧大概。

但是從公式可以看出，誤差損失和權重向量並沒有直接關係，這可咋辦，，，所以就用到了鏈式求導法則，不斷湊合本層所求的神經元相連線的各種函式，直到湊出來和權重有關。但是也不是瞎湊的。。。

因為和誤差損失直接相關的是輸出層函式，所以要從輸出層開始計算權重帶來的誤差損失然後逐漸往輸入方向求（即反向傳播）。所有誤差損失計算總誤差對權重求導，化簡後

後面求導為零。

因為和E1相關的權重只有w5和w6。所以只有第三項不一樣。

和E2相關的權重有w7和w8。

假設上面四個式子前面兩項為一個函式形式簡化表達：

至於為啥要簡化，，，自己一步一步推導之後發現後面很有用，求權重導數的時候很有規律。。。

直接寫結果：

然後後面那一項也有規律，，，

然後求w1-w4權重帶來的影響：

同樣求導：

這個地方有個小坑，因為把求導鏈式寫出之後，發現這是啥啊，這個誤差損失離w1這麼遠這怎麼算啊，還有這個裡面的誤差損失也不一樣，我看了文末的文獻之後才明白，原來這裡的誤差損失是總的損失，是E1和E2兩個輸出誤差損失共同作用的結果。

（1）

（2）

那麼問題又來了，這E1和E2和隱藏層隔得這麼遠這怎麼算對它的偏導啊，你讓我算輸出層的還行，隱藏層咋算。。。

所以這就是鏈式求導法則的妙處啊。。。就往最後一層輸出層的腳標使勁湊就行了。。。鏈式求導那一層的net對應那一層的out，同一個蘋果左右兩半下角標要一樣。o1對應h1，o2對應h2。並且和E1，E2對應。

突然發現前面兩項有點眼熟，就是a1和a2。上式化簡代入（1）和（2）中

有點對稱的感覺。

最後根據權重更新公式：

一直迭代，直到滿足目標為止。

import numpy as np
# "pd" 偏導
#b為偏值
#w為權重
#i為輸入資料
#target為目標資料
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def sigmoidDerivationx(y):
    return y * (1 - y)

if __name__ == "__main__":
	#初始化
	b = [0.35, 0.60]#偏值
	w = [0.15, 0.2, 0.25, 0.3, 0.4, 0.45, 0.5, 0.55]#權重
	i1 = 0.05
	i2 = 0.10
	target1 = 0.01
	target2 = 0.99
	alpha = 0.5 #學習速率
	numIter = 10000 #迭代次數
	for i in range(numIter):
		neth1 = i1*w[0] + i2*w[1] + b[0]#正向傳播
		neth2 = i1*w[2] + i2*w[3] + b[0]
		outh1 = sigmoid(neth1)
		outh2 = sigmoid(neth2)
		neto1 = outh1 * w[4] + outh2 * w[5]
		neto2 = outh1 * w[6] + outh2 * w[7]
		outo1 = sigmoid(neto1)
		outo2 = sigmoid(neto2)
		print("Interation:{} target1 is {},output1 is{};target2 is {},output2 is {}".format(i,target1,outo1,target2,outo2))
		#反向傳播更新權重w5-w8
		E1 = (target1 - outo1)**2/2
		E2 = (target2 - outo2)**2/2
		pdE1outo1 = - (target1 - outo1)
		pdE2outo2 = - (target2 - outo2)
		pdouto1neto1 = sigmoidDerivationx(outo1)#就是y(1-y)
		pdouto2neto2 = sigmoidDerivationx(outo2)
		pdneto1w5 = outh1
		pdneto1w6 = outh2
		pdneto2w7 = outh1
		pdneto2w8 = outh2
		a1 = pdE1outo1 * pdouto1neto1 #為簡化運算將鏈式求導前兩項簡化為a函式
		a2 = pdE2outo2 * pdouto2neto2
		pdE1w5 = a1 * pdneto1w5
		pdE1w6 = a1 * pdneto1w6
		pdE2w7 = a2 * pdneto2w7
		pdE2w8 = a2 * pdneto2w8
		#更新w1-w4權重
		pdouth1neth1 = sigmoidDerivationx(outh1)#此時為outh1(1-outh1)
		pdouth2neth2 = sigmoidDerivationx(outh2)
		pdEw1 = (a1*w[5-1] + a2*w[7-1])*pdouth1neth1*i1
		pdEw2 = (a1*w[5-1] + a2*w[7-1])*pdouth1neth1*i2
		pdEw3 = (a2*w[6-1] + a2*w[8-1])*pdouth2neth2*i1
		pdEw4 = (a2*w[6-1] + a2*w[8-1])*pdouth2neth2*i2
		w[0] = w[0] - alpha * pdEw1
		w[1] = w[1] - alpha * pdEw2
		w[2] = w[2] - alpha * pdEw3
		w[3] = w[3] - alpha * pdEw4
		w[4] = w[4] - alpha * pdE1w5
		w[5] = w[5] - alpha * pdE1w6
		w[6] = w[6] - alpha * pdE2w7
		w[7] = w[7] - alpha * pdE2w8
print("Finally output1 is {}; output2 is {}".format(outo1,outo2))
for j in range(8):
	print("{} is : {}.".format("w{}".format(j+1),w[j]))

參考來源：

https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/

英文搬運

https://www.cnblogs.com/charlotte77/p/5629865.html

中文搬運