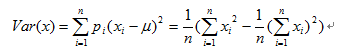影象處理之積分圖應用二(快速邊緣保留濾波演算法)
阿新 • • 發佈：2018-11-11
影象處理之積分圖應用二(快速邊緣保留濾波演算法)
一：基本原理
傳統的影象邊緣保留濾波演算法-如高斯雙邊模糊、Mean-Shift模糊等計算複雜、效率比較低，雖然有各種手段優化或者快速計算方法，當時演算法相對一般碼農來說理解起來比較費勁，不是一個的選擇，而通過積分影象實現區域性均方差的邊緣保留模糊演算法，計算簡單而且可以做到計算量跟半徑無關、跟上面提到兩種邊緣保留濾波(EPF)演算法效率高很多。首先區域性均方差濾波中計算區域性均值的公式如下：
當邊緣很弱的時候係數K趨近於0、該點的矯正之後的畫素值就接近平均值。而當邊緣很強的時候係數K趨近於1、該點的模糊之後的畫素值就接近等於輸入畫素值。上述計算中最中意的是視窗內畫素的均值與方差，計算均值可以根據積分影象很容易得到，而計算方差根據一系列的數學推導可以得到如下：
就是說可以根據積分影象通過常量次數的計算得到區域性的均值與方差，讓這種情況下的濾波變成一個常量時間完成的操作與視窗半徑大小無關。
二：演算法流程
1. 根據輸入的影象計算得到積分影象，參見《影象處理之積分影象演算法》
2. 根據輸入的半徑大小計算視窗內畫素均值與方差、計算得到每個畫素新的畫素值
3. 迴圈每個個畫素，重複第2步計算，得到最終的區域性均方差濾波影象
三：程式碼實現
-
package com.gloomyfish.ii.demo;
-
-
import java.awt.image.BufferedImage;
-
-
/**
-
* fast edge preserve filter algorithm base on integral image
-
* @author
-
* @E-mail:[email protected]
-
*
-
*/
-
public
class FastEPFilter extends AbstractImageOptionFilter {
-
// 視窗半徑大小
-
private
int xr;
-
private
int yr;
-
private
float sigma;
-
public FastEPFilter() {
-
}
-
-
public void setWinsize(int radius) {
-
this.xr = radius;
-
this.yr = radius;
-
}
-
-
public float getSigma() {
-
return sigma;
-
}
-
-
public void setSigma(float sigma) {
-
this.sigma = sigma;
-
}
-
-
@Override
-
public BufferedImage process(BufferedImage image) {
-
long time = System.currentTimeMillis();
-
int width = image.getWidth();
-
int height = image.getHeight();
-
// get image data
-
int[] pixels =
new
int[width * height];
-
int[] outPixels =
new
int[width * height];
-
getRGB(image,
0,
0, width, height, pixels);
-
int size = (xr *
2 +
1) * (yr *
2 +
1);
-
int r =
0, g =
0, b =
0;
-
float sigma2 = sigma*sigma;
-
-
// per-calculate integral image
-
byte[] R =
new
byte[width*height];
-
byte[] G =
new
byte[width*height];
-
byte[] B =
new
byte[width*height];
-
getRGB(width, height, pixels, R, G, B);
-
IntIntegralImage rii =
new IntIntegralImage();
-
rii.setImage(R);
-
rii.process(width, height);
-
IntIntegralImage gii =
new IntIntegralImage();
-
gii.setImage(G);
-
gii.process(width, height);
-
IntIntegralImage bii =
new IntIntegralImage();
-
bii.setImage(B);
-
bii.process(width, height);
-
int index =
0;
-
-
for (
int row = yr; row < height - yr; row++) {
-
for (
int col = xr; col < width - xr; col++) {
-
index = row * width + col;
-
r = ((pixels[index] >>
16) &
0xff);
-
g = (pixels[index] >>
8) &
0xff;
-
b = (pixels[index] &
0xff);
-
-
int sr = rii.getBlockSum(col, row, (yr *
2 +
1), (xr *
2 +
1));
-
int sg = gii.getBlockSum(col, row, (yr *
2 +
1), (xr *
2 +
1));
-
int sb = bii.getBlockSum(col, row, (yr *
2 +
1), (xr *
2 +
1));
-
-
float vr = rii.getBlockSquareSum(col, row, (yr *
2 +
1), (xr *
2 +
1));
-
float vg = gii.getBlockSquareSum(col, row, (yr *
2 +
1), (xr *
2 +
1));
-
float vb = bii.getBlockSquareSum(col, row, (yr *
2 +
1), (xr *
2 +
1));
-
-
// 計算均值
-
float mr = sr / size;
-
float mg = sg / size;
-
float mb = sb / size;
-
-
// 計算方差
-
float dr = (vr - (sr*sr)/size)/size;
-
float dg = (vg - (sg*sg)/size)/size;
-
float db = (vb - (sb*sb)/size)/size;
-
-
// 計算係數K
-
float kr = dr / (dr+sigma2);
-
float kg = dg / (dg+sigma2);
-
float kb = db / (db+sigma2);
-
-
// 得到濾波後的畫素值
-
r = (
int)((
1-kr)*mr + kr*r);
-
g = (
int)((
1-kg)*mg + kg*g);
-
b = (
int)((
1-kb)*mb + kb*b);
-
-
outPixels[row * width + col] = (
0xff <<
24) | (clamp(r) <<
16) | (clamp(g) <<
8) | clamp(b);
-
}
-
}
-
System.out.println(
"FastEPFilter ->> time duration : " + (System.currentTimeMillis() - time));
-
BufferedImage dest =
new BufferedImage(width, height, BufferedImage.TYPE_INT_ARGB);
-
setRGB(dest,
0,
0, width, height, outPixels);
-
return dest;
-
}
-
-
/** Returns the red, green and blue planes as 3 byte arrays. */
-
public void getRGB(int width, int height, int[] pixels, byte[] R, byte[] G, byte[] B) {
-
int c, r, g, b;
-
for (
int i=
0; i < width*height; i++) {
-
c = pixels[i];
-
r = (c&
0xff0000)>>
16;
-
g = (c&
0xff00)>>
8;
-
b = c&
0xff;
-
R[i] = (
byte)r;
-
G[i] = (
byte)g;
-
B[i] = (
byte)b;
-
}
-
}
-
-
}
四：執行效果
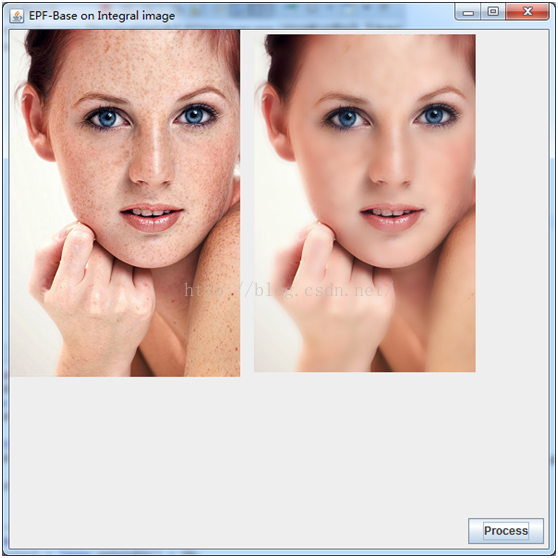
半徑設定為5，即視窗大小為5的時候，調整引數sigma的值即可得到此效果
其實很多磨皮的演算法都是基於這個演算法實現的，這個才是我想說的重點，
只有耐心看到此處才可以得到正確的答案。
五：參考：
http://imagej.net/Integral_Image_Filters#Variance
http://www.activovision.com/octavi/doku.php?id=integral_images