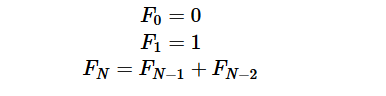1. 斐波那契數列

費波那契數列（義大利語：Successione di Fibonacci），又譯為費波拿契數、斐波那契數列、費氏數列。
在數學上，費波那契數列是以遞迴的方法來定義：

當n趨近於無窮大時，後一項與前一項的比值趨近於1.618，因此也叫黃金比例數列。

斐波那契寫書時以兔子繁殖問題為例子，因此也叫兔子繁殖數列。

2.斐波那契Java實現

package atOffer_09;

import java.util.Scanner;

public class Fibonacci {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		
		Scanner sc = new Scanner(System.in);
		int num = sc.nextInt();
		System.out.println(fibonacci(num));
		sc.close();

	}
	
	private static int fibonacci(int num) {
		int[] result = new int[] {0,1};
		if(num < 2)
			return result[num];
		int fibonacciMinus2 = result[0];
		int fibonacciMinus1 = result[1];
		int fibonacciNum = 1;
		
		for(int i = 2; i <= num; i++) {
			fibonacciNum = fibonacciMinus1 + fibonacciMinus2;
			fibonacciMinus2 = fibonacciMinus1;
			fibonacciMinus1 = fibonacciNum;
		}
		
		return fibonacciNum;
	}

}
 

確認前兩項線性實現，效率比遞迴快

3.跳臺階問題

問題描述：一隻青蛙一次可以跳上 1 級臺階，也可以跳上2 級。求該青蛙跳上一個n 級的臺階總共有多少種跳法。

設f(n)表示青蛙跳上n級臺階的跳法數。當只有一個臺階時，
即n = 1時， 只有1種跳法；
當n = 2時，有兩種跳法；
當n = 3 時，有3種跳法；
當n很大時，青蛙在最後一步跳到第n級臺階時，有兩種情況：
一種是青蛙在第n-1個臺階跳一個臺階，那麼青蛙完成前面n-1個臺階，就有f(n-1)種跳法，這是一個子問題。
另一種是青蛙在第n-2個臺階跳兩個臺階到第n個臺階，那麼青蛙完成前面n-2個臺階，就有f(n-2)種情況，這又是另外一個子問題。所以這種問題實質上就是斐波那契數列問題，用公式表達為：

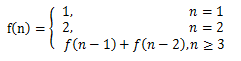
用程式碼實現和斐波那契相同：

package atOffer_09;

import java.util.Scanner;

public class JumpFloor {

	public static void main(String[] args) {
		// TODO Auto-generated method stub

		Scanner sc = new Scanner(System.in);
		int num = sc.nextInt();
		System.out .println(JumpSteps(num));
		sc.close();
	}
	
	private static int JumpSteps(int num) {
		int[] jump = new int[] {0,1};
		if(num < 2) {
			return jump[num];
		}
		
		int jumpMinus1 = jump[1];
		int jumpMinus2 = jump[0];
		int jumpStep = 1;
		
		for(int i = 2; i <= num; i++) {
			jumpStep = jumpMinus1 + jumpMinus2;
			jumpMinus2 = jumpMinus1;
			jumpMinus1 = jumpStep;
		}
		
		return jumpStep;
	}

}
 

4.問題變型

變態跳臺階指一隻青蛙可以一次跳任意階臺階，求問跳n階臺階的方法，解決方法思想也可以規劃為寫公式讓斐波那契求解的過程，跳n階的時候即f(n) = f(n-1)+f(n-2)+...+f(2)+f(1)+1=2^(n-1)種方法

兔子繁殖問題是斐波那契經典問題解決方法同理。

矩形覆蓋問題：我們可以用2*1的小矩形橫著或者豎著去覆蓋更大的矩形。
 請問用n個2*1的小矩形無重疊地覆蓋一個2*n的大矩形，總共有多少種方法？同理

參考文獻：

【1】https://blog.csdn.net/K346K346/article/details/52576680

【2】https://zh.wikipedia.org/wiki/%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97#%E5%92%8C%E9%BB%83%E9%87%91%E5%88%86%E5%89%B2%E7%9A%84%E9%97%9C%E4%BF%82