學習鄰接表存圖請看：https://blog.csdn.net/HPU_FRDHR/article/details/83957240

 DFS （深度優先搜尋）

       深度優先搜尋演算法（英語：Depth-First-Search，簡稱DFS）是一種用於遍歷或搜尋樹或圖的演算法。 沿著樹的深度遍歷樹的節點，儘可能深的搜尋樹的分支。當節點v的所在邊都己被探尋過或者在搜尋時結點不滿足條件，搜尋將回溯到發現節點v的那條邊的起始節點。整個程序反覆進行直到所有節點都被訪問為止。屬於盲目搜尋,最糟糕的情況演算法時間複雜度為O(!n)。

演算法步驟： 

按如下將圖存好後開始遍歷：

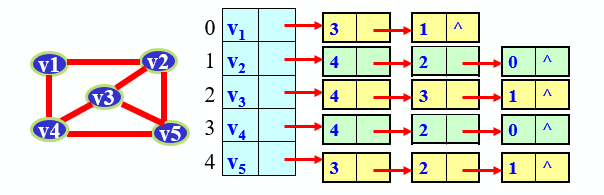
1.在訪問圖中某一起始頂點 v 後，由 v 出發，訪問它的任一鄰接頂點 w1；

2.再從 w1 出發，訪問與 w1鄰接但還未被訪問過的頂點 w2；

3.然後再從 w2 出發，進行類似的訪問，…，如果w2後所有的節點都被訪問過了，接著，退回一步，退到前一次剛訪問過的頂點，看是否還有其它沒有被訪問的鄰接頂點，即回溯到前一個節點w1繼續訪問。

4.如此進行下去，直至到達所有的鄰接頂點都被訪問過的頂點 u 為止。

 程式碼實現：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
using namespace std;

#define OK 1
#define MVNum 100								//最大頂點數 

typedef int Status;
typedef int OtherInfo;
typedef char VerTexType;

Status visited[MVNum];							//訪問標誌陣列，其初值為0 

typedef struct ArcNode{							//邊節點
	int adjvex;									//該邊所指向的在頂點的位置 
	struct ArcNode * nextarc;					//指向下一條邊的指標 
	OtherInfo info;								//和邊相關的資訊 
}ArcNode;

typedef struct Vnode{							//頂點資訊 
	VerTexType data;
	ArcNode *firstarc;							//指向第一條依附該頂點的指標 
}VNode,AdjList[MVNum];							//AdjList表示鄰接表型別
 
typedef struct{
	AdjList vertices;
	int vexnum,arcnum;							//圖當前的頂點數和邊數 
}ALGraph;

//確定v在G中的位置，即頂點在G.vertices中的序號 
Status LocateVex(ALGraph G,char v){
	int i;
	for(i=0;i<G.vexnum;i++){
		if(v==G.vertices[i].data)
		    return i;
	}
}

//鄰接表法建立無向圖 
Status CreateUDG(ALGraph &G){
	Status i,j,k; 
	char v1,v2;
	ArcNode *p1,*p2;
	cout<<"請輸入總頂點數 總邊數:"; 
	cin>>G.vexnum>>G.arcnum;					//輸入總頂點數總邊數
	puts("請輸入頂點資訊:");
	for(i=0;i<G.vexnum;++i){					//輸入各點，構造表頭節點表
		cin>>G.vertices[i].data;				//輸入頂點值
		G.vertices[i].firstarc=NULL;			//初始化表頭節點的指標域為NULL
	}
	puts("請輸入每一條邊對應的兩個頂點:");
	for(k=0;k<G.arcnum;++k){					//輸入各邊，構造鄰接表
		cin>>v1>>v2;							//輸入一條邊依附的兩個頂點
		i=LocateVex(G,v1);
		j=LocateVex(G,v2);
		p1=new ArcNode;							//生成一個新的邊節點*p1
		p1->adjvex=j;							//鄰接點序號為j
		p1->nextarc=G.vertices[i].firstarc;		//將新節點*p1插入頂點vi的邊表頭 
		G.vertices[i].firstarc=p1;
		p2=new ArcNode;							//生成一個新的邊節點*p2
		p2->adjvex=i;							//鄰接點序號為i
		p2->nextarc=G.vertices[j].firstarc;		//將新節點*p2插入頂點vj的邊表頭
		G.vertices[j].firstarc=p2;
	}
	return OK;
}

//列印鄰接表儲存資料
void print_position(ALGraph G){
	int i;
	for(i=0;i<G.vexnum;i++){
		ArcNode p;
		p.adjvex=G.vertices[i].firstarc->adjvex;
		p.nextarc=G.vertices[i].firstarc->nextarc;
		printf("%c->",G.vertices[i].data);
		while(p.nextarc!=NULL){
			printf("%c -> ",G.vertices[p.adjvex].data);
			p=*p.nextarc;
		}
		printf("%c\n",G.vertices[p.adjvex].data);
	} 
}

//遞迴實現從第v個頂點出發深度優先搜尋遍歷圖G
void DFS_AL(ALGraph G,int v){
	ArcNode *p;
	int w;
	printf("%c ",G.vertices[v].data);			//訪問第v個頂點
	visited[v]=1;								//置訪問標誌陣列相應分量值為1
	p=G.vertices[v] .firstarc;					//p指向v的邊連結串列的第一個邊結點
	while (p!=NULL){							//邊結點非空
		w=p->adjvex;							//表示w是V的鄰接點
		if(!visited[w])	DFS_AL(G,w);			//如果w未訪問，則遞迴呼叫DFS_ AL
		p=p->nextarc;							//p指向下一個邊結點
	}
}

//非遞迴實現從第v個頂點出發深度優先搜尋遍歷圖G
void DFS_ALL(ALGraph G,int v){
	memset(visited,0,sizeof(visited));
	stack<char> st;									//定義一個棧 
	ArcNode *p;
	int w,n,s;
	n=G.vexnum-1;
	printf("%c ",G.vertices[v].data);				//訪問第v個頂點
	st.push(G.vertices[v].data);					//將第v個頂點壓入棧中 
	visited[v]=1;									//置訪問標誌陣列相應分量值為1
	p=G.vertices[v] .firstarc;						//p指向v的邊連結串列的第一個邊結點
	while(n){
		int cnt=0;
		while(p!=NULL){								//邊結點非空
			w=p->adjvex;							//表示w是V的鄰接點
			if(!visited[w]){//如果w未訪問
				printf("%c ",G.vertices[w].data);
				st.push(G.vertices[w].data);
				visited[w]=1;
				cnt=1,n--;
				break;
			}else
				p=p->nextarc;
		}
		if(cnt==0)
			st.pop();
		s=LocateVex(G,st.top());
		p=G.vertices[s] .firstarc;
	}
} 

int main(){
	char s,k;
	int n,m; 
	memset(visited,0,sizeof(visited)); 
	ALGraph G;
	CreateUDG(G);
	puts("構建的鄰接表為：");
	print_position(G);
	puts("請輸入遞迴遍歷開始的起點："); 
	cin>>s;
	n=LocateVex(G,s);
	DFS_ALL(G,n);
	printf("\n");
	puts("請輸入非遞迴遍歷開始的起點：");
	cin>>k;
	m=LocateVex(G,k);
	DFS_ALL(G,m);
	return 0;
}