2. 程式人生 > >知識表示模型彙總分析--Trans系列

知識表示模型彙總分析--Trans系列

阿新 • • 發佈：2018-11-11

作者：孫天祥
連結：https://zhuanlan.zhihu.com/p/43436288
來源：知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。

因為還根據自己的理解補充了點兒內容，就標為原創了。下面是正文：
 

近年來，以深度學習為代表的表示學習迅速發展，在很多領域都取得了巨大進展。簡而言之，表示學習將要描述的物件表示為低維稠密向量，這也被稱為分散式表示，從而有效解決了資料稀疏問題，並且便於在低維語義空間中進行計算。將表示學習應用於知識圖譜（Knowledge Graph, KG），即是知識表示學習。

在當前的主流知識庫中，知識被儲存為 (h, r, t) 的三元組形式，其中 h

表示頭實體， r 表示聯絡， t 表示尾實體。知識表示學習的任務就是學習 h, r, t 的分散式表示（也被叫做知識圖譜的嵌入表示(embedding)）。

目前，知識表示學習方法從實現形式上可以分為兩類：基於結構的方法和基於語義的方法。基於結構的嵌入表示方法包括TransE, TransH, TransR&CTransR, TransD等，這類方法從三元組的結構出發學習KG的實體和聯絡的表示；基於語義的嵌入表示方法包括NTN, SSP, DKRL等，這類方法從文字語義的角度出發學習KG的實體和聯絡的表示。

知識表示學習從發展來看可以分成兩個階段，以2013年Borders等人受Mikolov發現的語義空間中詞向量的平移不變現象啟發，從而提出了翻譯模型
(TransE)為分割。在TransE之前，有Structed Embedding, Semantic Matching Energy等模型，在TransE之後，人們在此基礎上進行改進，依次提出了TransH, TransR, TransD等模型。接線來介紹基於TransE的改進模型。

作者：孫天祥
連結：https://zhuanlan.zhihu.com/p/43436288
來源：知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。
 

TransE


論文：Translating Embeddings for Modeling Multi-relational Data. Antoine Bordes, Nicolas Usunier, Alberto Garcia-Duran, Jason Weston, Oksana Yakhnenko. NIPS 2013.



我們用 h 表示頭實體向量，用 t 表示尾實體向量，用 r 表示關係向量，TransE模型的目標就是讓 t-h 儘可能地等於 r ，即 t-h\approx r 。其評分函式為：

f_r(h, t) = \lVert h+r-t\rVert _{L_1/L_2}

顯然，對於正確的三元組，應該有較低的得分。在訓練過程中，使用等級損失函式，這是因為在當前情況下我們沒有就標籤而言的監督，只有一對正確項 (h,r,t)\in \Delta 和不正確項 (h',r',t')\in \Delta' ，我們的目的是讓正確項的得分比不正確項高。這種情況出現在我們只有正例時，知識圖譜就是這種情況，我們只知道正確的三元組（golden triplet），再通過破壞一個正例來生成負例。等級損失就適用於這種情況，因此我們定義損失函式：

L = \sum_{(h,r,t)\in \Delta}\sum_{(h',r',t')\in \Delta'}\max (f_r(h,t)+\gamma -f_{r'}(h',t'),0).

上式中的 \gamma 表示正例和負例得分的最小間隔(margin)，實際使用時常取 \gamma=1 .

博主注：

我們的目標是讓f(h,t)最小，讓f(h',t')最大。開始我覺得上面的公式不對，因為應該是取上式的極小值作為目標函式。後來想了想，上式僅僅是損失函式，表示的是總體損失。式中的max不是對目標函式取max，而是對於每一對正反例，取f(h,t)+v-f(h',t')和0中的最大值，以免出現負值。

避免出現負值的原因：如果某一項是負的，那麼可以通過使得這個負值的模非常大，來使得整個公式的值是一個模非常大的負值。而這樣顯然不是我們想要的。這樣僅僅使得某一項符合要求，並不是全域性最優。

如果我自己設計一個公式，估計是不能想到這一點的。看來頂會論文的水平還是很高的，方法既新奇又滴水不漏。
 

事實上，將等級損失中的得分函式替換為樣本被預測為某個類別的概率，則上式的形式與多分類情形下的hinge損失一致。


TransE採取的生成負例三元組的方法是，將正確的三元組的頭實體、尾實體、關係三者之一隨機替換為其他實體或關係，從而構成負例集合 \Delta' ，這種方法稱為均勻取樣（與後面的伯努利取樣相對比）。

在程式碼實現中，首先選取一個正例三元組 (h,r,t) ，再從 \Delta' 中取樣得到一個負例三元組 (h',r',t') ，然後分別計算正例得分 f_r(h,t) 和負例得分 f_{r'}(h',t') ，若 f_r(h,t)+\gamma -f_{r'}(h',t')>0 ，則梯度下降更新 h,r,t,h',r',t' .

顯然，TransE模型在處理複雜關係建模（一對多、多對一、多對多關係）時會遇到困難，例如，對於一對多關係（美國，總統，奧巴馬）和（美國，總統，特朗普），TransE模型會使得尾實體向量奧巴馬和特朗普的表示非常相似。事實上，這是由於對於不同的關係 r ，實體向量的表示總是相同的。


TransH


論文：Knowledge Graph Embedding by Translating on Hyperplanes. Zhen Wang, Jianwen Zhang, Jianlin Feng, Zheng Chen. AAAI 2014.

TransH方法由中山大學信科院馮劍琳團隊和MSRA聯合提出，克服了TransE模型的上述缺點，使得同一個實體向量在不同關係下有不同的表示。

TransH模型對於每一個關係 r ，假設有一個對應的超平面（關係 r 落於該超平面上），其法向量為 w_r ，且有 \lVert w_r\rVert_2=1 . 關於超平面，可以參見這裡。

類似於TransE模型的翻譯在該超平面上進行，具體地，首先將頭實體 h 和尾實體 t 投影到該超平面上得到 h_\perp 和 t_\perp ，即

h_\perp = h-w_r^Thw_r,

t_\perp = t-w_r^Ttw_r.

博主注：

上述公式可以將h和t進行投影。以h為例，其中的wT*h是一個數，是將h投影到w方向的向量的模。後面再乘一個w是為了把這個標量變成向量。這樣的話，h與這個向量的差就是h在超平面上的投影向量。

進而，我們定義得分函式為

f_r(h,t) = \lVert h_\perp +r - t_\perp \rVert _{L_1/L_2}

原文中貼出了一張圖，很直觀的說明了TranH的工作原理，以及和TransE的區別。


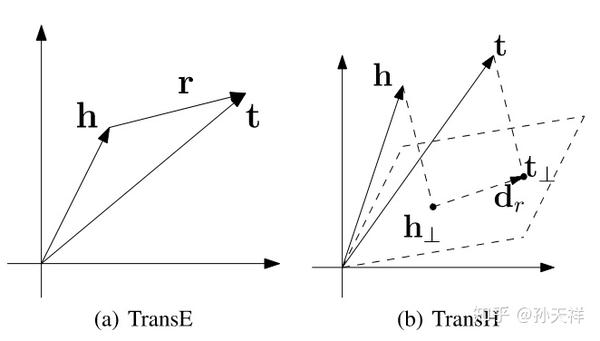
博主注：

考慮之前總統的例子，也就是一個一對多的問題。將關係表示成超平面後，這種問題得到了解決。如下圖所示，如果分別用t和t‘表示兩個總統，那麼將三元組對映到超平面之後，t和t‘都能滿足’（美國，總統，*）這個三元組。並且兩個向量在向量空間還是不同的。多對一，多對多的情況也可以這樣解決。

當然，投影后我們需要訓練的引數就不止是實體和關係向量了。還得訓練投影平面（其實就是每個關係對應的投影平面的法向量）。目標函式變為：

其中[]+表示的就是TransE公式中的max（*，0），即對於中括號中的值，返回0和它之間的最大值。

上式還得滿足三個限制。其中，限制（1）保證每個向量的模都小於1。限制（2）是dr到wr的投影長度/dr的長度，這個值非常小，保證了dr確實在投影平面上。限制（3）規定投影平面的法向量的模為1，這樣做是為了簡化公式h_\perp = h-w_r^Thw_r,。否則這個公式的形式就會更為複雜。

雖然TransH模型使得同一實體在不同關係下通過投影有了不同的表示，但投影之後仍然處於原來的空間 \mathbb R^n 中，這裡 n 表示實體向量和關係向量均為 n 維。換言之，TransH模型假設實體和關係處於相同的語義空間中，這在一定程度上限制了它的表示能力。下面的TransR模型改進了這一缺陷，提高了模型的表示能力。

值得一提的是，在本篇論文中除了提出了TranH模型，另一貢獻是提出了基於伯努利分佈的取樣方法。在原來的均勻取樣中，容易將錯誤的負例引入到訓練過程中來，例如，對於正例（美國，總統，奧巴馬），隨機替換奧巴馬為羅斯福構成（美國，總統，羅斯福）作為負例，實際上由於羅斯福也是總統，這並不是一個負例。新的取樣方法的動機是，對於一對多關係，我們以更大的概率來替換其頭實體，對於多對一關係，我們以更大的概率來替換其尾實體。具體地，對於包含關係 r 的所有三元組，我們定義兩個統計量：

1. tph : 平均每個頭實體對應多少個尾實體
2. hpt : 平均每個尾實體對應多少個頭實體

進而，取伯努利分佈的引數為 p=\frac{tph}{tph+hpt} ，即以概率 p 替換三元組的頭實體，以概率 1-p 替換三元組的尾實體。實際上， p 反映了一對多關係的失衡程度。

博主注：

可以先忽略分母（分母是用來歸一化的）。那麼，tph表示一個頭實體大概對應多少尾實體。這個值越大說明我們在構建負例時，固定頭實體，隨機選擇尾實體的過程中越可能出錯（一不小心就弄成正例了）。所以這時候我們應該替換頭實體。因此歸一化的tph就是替換頭實體的概率。相似地，歸一化的hpt就是替換尾實體的概率。
通過基於伯努利分佈的取樣，我們就降低了引入錯誤的負例的概率。在清華大學NLP組的開原始碼KB2E中，同時提供了兩種取樣方式，bern表示伯努利取樣，unif表示均勻取樣。

TransR & CTransR


論文：Learning Entity and Relation Embeddings for Knowledge Graph Completion. Yankai Lin, Zhiyuan Liu, Maosong Sun, Yang Liu, Xuan Zhu. AAAI 2015.


TransR


TransR模型是由清華大學NLP組（林衍凱、劉知遠、孫茂松等）提出，TransR模型認為，不同的關係關注實體的不同屬性（實體向量的不同維度），因此不同的關係應具有不同的語義空間。

TransH模型是為每個關係假定一超平面，將實體投影到這個超平面上進行翻譯；而TransR模型是為每個關係假定一語義空間 \mathbb R^m ，將實體對映到這個語義空間上進行翻譯。這裡 m 表示關係向量的維度為 m 。

TransR模型可以形式化描述為

h_r = hM_r,\ \ t_r = tM_r, 

f_r(h,t) = \lVert h_r +r -t_r\rVert _{L_1/L_2}. 

其中， h,t\in \mathbb R^n, r\in \mathbb R^m, M_r\in \mathbb R^{n\times m} . 約束條件為 h,t,h_r,t_r,r 的L2範數均不大於1.


CTransR


CTransR的意思是Cluster-based TransR. CTransR對於每一個特定的關係 r ，首先根據實體對 (h,t) 進行AP聚類（一種不需要指定類別數的聚類方法），實際上是對實體對的差值向量 h-t 進行聚類，從而將關係 r 分解為更細粒度的子關係 r_c ，CTransR對每個 r_c 分別學習相應的向量表示。

形式化地，CTransR的得分函式可以描述為

f_r(h,t) = \lVert h_{r,c}+r_c-t_{r,c}\rVert _2^2 + \alpha \lVert r_c - r \rVert _2 ^2. 

上式中第二項使得 r_c 儘可能地接近 r . 

TransR & CTransR模型將原來的單個語義空間分離為實體空間和關係空間，提高了模型的表示能力，然而，TransR模型仍然存在一些缺點：

1. 在同一個關係 r 下，頭、尾實體使用相同的投影矩陣 M_r ，而頭、尾實體可能型別或屬性相差很大；

2. 投影矩陣僅與關係有關；

3. 引數多，計算複雜度高。


TransD


論文：Knowledge Graph Embedding via Dynamic Mapping Matrix. Guoliang Ji, Shizhu He, Liheng Xu, Kang Liu, Jun Zhao. ACL 2015.

TransD模型由中科院自動化所NLPR中趙軍、劉康組提出，一定程度上克服了TransR & CTransR的上述缺點。

CTransR模型相比於TransR模型，實際上就是考慮了同一個關係也有不同的型別，然而，實體也有不同的型別。舉個例子，在FB15k中，有關係location.location.partially containedby，它可以表示山川大河被某個國家包含，也可以表示山川大河被某個城市/州包含，也可以表示國家被大洲包含，還可以表示地區被國家包含。由於實體有不同的型別，因而使用相同的對映矩陣是不合理的，而且，對映矩陣不應只與關係有關，還應與頭尾實體有關。以上就是TransD模型的動機，這實際上是一個更細粒度的擴充套件模型，本質上還是由實體語義空間和關係語義空間兩個空間構成。

具體地，對於一個三元組 (h,r,t) ，分別定義對應的投影向量 h_p,r_p,t_p ，其中 p 表示投影（projection），再定義兩個投影矩陣 M_{rh}, M_{rt} 來將實體從實體空間對映到關係空間。

M_{rh}=r_ph_p^T+I^{m\times n} 

M_{rt}=r_pt_p^T+I^{m\times n} 

這裡， r_p,r\in \mathbb R^m, h,h_p,t,t_p\in \mathbb R^n , M_{rh}, M_{rt}\in \mathbb R^{m\times n} ， I^{m\times n} 表示單位陣，它的意思是說用單位陣來初始化投影矩陣。

Tips: 如果你檢查過向量和矩陣的維度，可能會發現在TransD中，實體和關係向量均為列向量，而在前面的模型中實體和關係都是行向量。這裡尊重了原文中的形式，並未在本文中做統一。


可見，在上式中，對頭實體應用投影矩陣 M_{rh} ，它不僅與關係有關，還與頭實體有關；對尾實體應用投影矩陣 M_{rt} ，它也不僅與關係有關，還與尾實體有關。利用這兩個投影矩陣，可以得到頭實體和尾實體在關係空間的投影

h_\perp =M_{rh}h,\ \ t_\perp = M_{rt}t 

從而得分函式為

f_r(h,t) = \lVert h_\perp +r - t_\perp \rVert _{L_1/L_2}


對比


理論對比


顯然，TransE是TransD的一個特例，當 m=n 且所有投影向量均為零時，TransD就退化為了TransE. 與TransH對比，顯然需先令TransD的 m=n ，再分別寫出TransH和TransD的實體投影后的向量：

\mathrm{TransH:}\ \ h_\perp = h-w_r^Thw_r, 

\mathrm{TransD:}\ \ h_\perp =M_{rh}h=h+h_p^Thr_p 

因為 r_ph_p^Th=h_p^Thr_p ，因此為便於格式上的對比，我們將TransD中的 h_\perp 寫成上述形式。可見，當 m=n 時，TransD與TransH唯一的區別在於TransD中的投影向量不僅與關係有關，還與實體有關。

對比TransR模型，TransD為頭實體和尾實體分別設定了投影矩陣，另外，注意到在TransD中公式經過展開之後沒有矩陣-向量乘法操作，這相比於TransR模型降低了計算複雜度，更適用於大規模知識圖譜的計算。


效能對比


評估不同知識表示學習方法的優劣的主要指標就是在知識圖譜的一些典型任務上的表現，比如三元組分類（triplet classification）和連結預測（link prediction）。下面貼出在WordNet和Freebase中各模型在兩任務上的表現，TransE, TransH, TransR, CTransR, TransD包括了使用bern和unif取樣的結果。圖片資料來源於TransD的論文。
 

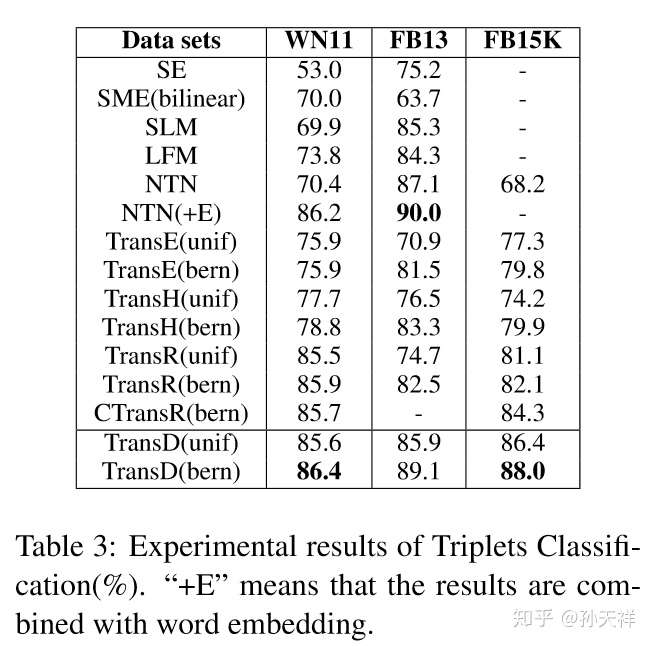
三元組分類結果對比

 

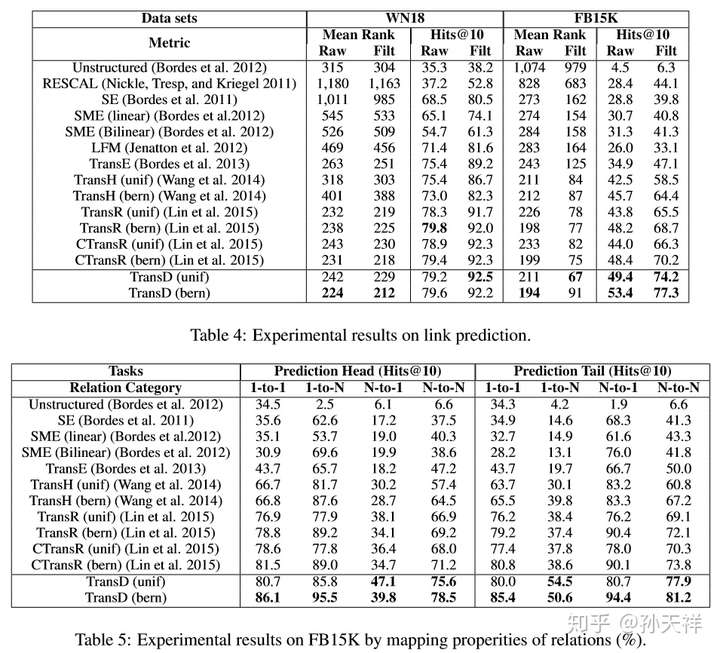
連結預測結果對比

相關推薦

知識表示模型彙總分析--Trans系列

作者：孫天祥 連結：https://zhuanlan.zhihu.com/p/43436288 來源：知乎 著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。 因為還根據自己的理解補充了點兒內容，就標為原創了。下面是正文：   近年來，以深度學習為代表的表示學

【軟考】軟體開發模型彙總分析

軟體開發模型 瀑布模型 將生命週期中的各個活動規定為以線性順序連結的若干階段的模型，包括需求分析、設計、編碼、測試、執行與維護，它規定由前至後的順序次序，就像瀑布流水一樣逐級下落 小明來解說：小明的媽媽要小明去買東西（薯片，爆米花，烤紅薯，糖炒栗子），瀑布模型就是，小明在家裡

oracle分析函式系列之sum(col1) over(partition by col2 order by col3):實現分組彙總或遞增彙總

語法:sum(col1) over(partition by col2 order by col3 )  準備資料:    DEPT_ID    ENAME          SAL 1 1000            A                     2500

Tomcat7源碼分析學習系列之一-----tomcat的啟動文件startup的註釋

addition mission etl %0 很好 fine copy 文件結尾 存在 1. Windows系統，tomcat啟動文件startup.bat @echo off 　　　　　　rem 關閉回顯，不顯示下面的命令；rem Licensed to the Apa

數據模型圖解分析(用戶訂單商品)

items ora 設置 code ems image item http 分享 對訂單商品數據模型進行分析 數據模型分析思路 1 每張表記錄的數據內容 　　　　分模塊對每張表記錄的內容進行熟悉，相當於你學習系統需求(功能)的過程。 2 每張表重要字段設置 　

軟件工程--常用軟件開發模型比較分析

開發模型 軟件工程 正如任何事物一樣，軟件也有其孕育、誕生、成長、成熟和衰亡的生存過程，一般稱其為“軟件生命周期”。軟件生命周期一般分為6個階段，即制定計劃、需求分析、設計、編碼、測試、運行和維護。軟件開發的各個階段之間的關系不可能是順序且線性的，而應該是帶有反饋的叠代過程。在軟件工程中，這個復雜的過

文本深度表示模型Word2Vec

ear get cursor .sh del 概率 ack art bin 簡介Word2vec 是 Google 在 2013 年年中開源的一款將詞表征為實數值向量的高效工具, 其利用深度學習的思想，可以通過訓練，把對文本內容的處理簡化為 K 維向量空間中的向量運算，而向

[Algorithm & NLP] 文本深度表示模型——word2vec&doc2vec詞向量模型

www. 頻率 cbo homepage 算法 文章 有一個 tro 概率 閱讀目錄 1. 詞向量 2.Distributed representation詞向量表示 3.詞向量模型 4.word2vec算法思想 5.doc2vec算法思

Java內存模型之分析volatile

b- oid HR 變量 before 深入 lba 避免 har 前篇博客【死磕Java並發】—–深入分析volatile的實現原理 中已經闡述了volatile的特性了： volatile可見性；對一個volatile的讀，總可以看到對這個變量最終的寫； volati

第一次作業：關於Linux進程模型的分析

inux .html 符號 搶占 等待 資料 除了 idl aml 1、前言 本文主要基於Linux Kernel 2.6.32 的源碼,對Linux的進程模型進行分析，大致可以概括為如下內容： 1.前言 2.進程介紹 3.操作系統如何組織進程 4.進程狀態的轉化 5.進程

python並發編程：IO模型比較分析

inf png 檢查 mod model roc io操作 rdquo 進程 blocking和non-blocking的區別在哪，synchronous IO和asynchronous IO的區別在哪。 blocking vs non-blocking：調用blocki

word2vec 中的數學原理三 背景知識 語言模型

tps 詳解 art 技術 nbsp log 分享圖片 word2vec 自己 主要參考： word2vec 中的數學原理詳解 自己動手寫 word2vec word2vec 中的數學原理三 背景知識 語言模型

Holt-Winters模型原理分析

實驗室 研究 top 發現 總結 分析 The 如果 選擇權 Holt-Winters模型原理分析及代碼實現（python) from：https://blog.csdn.net/u010665216/article/details/78051192 引言 最近

Light Weight CNN模型的分析與總結

翻譯 sem ict edi bcb sin rar 線性 更多 本文選擇了4個light weight CNN模型，並對它們的設計思路和性能進行了分析與總結，目的在於為在完成圖像識別任務時模型的選擇與設計方面提供相關的參考資料。 1 簡介 自AlexNet[1]在LSVR

關於React的Container&Presentational Component模型結構分析

數量 傳遞 index 行數 決定 one pbo widget 一個人 react.js javascript 3 之前翻譯了兩篇關於Container&Presentational Component模型的文章，一篇是基

ADO.Net之SqlConnection、 Sqlcommand的應用學習心得（思維導圖，知識解析，案例分析）

ros statistic system 啟動 clone() 連接字符串 esp ans 用戶 ADO.Net之SqlConnection、 Sqlcommand的應用 一、思維導圖： ADO.NET與SQL連接： 二、知識點介紹： SqlConnecti

知識表示學習1多元關係資料翻譯嵌入2知識表示學習關係路徑建模(公號回覆“知識表示學習”下載彩標PDF典藏版資料)

知識表示學習1多元關係資料翻譯嵌入2知識表示學習關係路徑建模(公號回覆“知識表示學習”下載彩標PDF典藏版資料) 原創： 秦隴紀 資料簡化DataSimp 今天 資料簡化DataSimp導讀：醫學AI讀書會兩篇論文：[1]Bordes A, Usunier N, Garcia-Dur

Unity 數學知識——數學公式彙總

在做智慧家居設計軟體的時候用到的常規數學公式，彙總在這裡給大家作參考。     插入排序  /// <summary>     /// 插入排序_列表     /// </summary>

UnityShader開發之光照 - 簡單光照模型 - Phong反射光模型引數分析

1.概念 light color = emissive + ambient + diffuse + specluar emissive：自發光 ambient：環境光 diffuse ：漫反射光 specluar：鏡面光   Phong模型 鏡面光公式

數極客釋出第10大使用者行為資料分析模型-間隔分析

數極客釋出第10大使用者行為資料分析模型-間隔分析 一、什麼是間隔分析？ 在我們分析使用者轉化行為時，除了利用數極客的6大轉化率分析和提升模型之外，我們還會關注使用者完成轉化所需的時長，數極客間隔分析模型通過任意兩個行為之間的時長間隔分析，可以掌握使用者完成轉化的效率，分析使用者體驗是否存在問題。