20172313 2018-2019-1 《程式設計與資料結構》第五週學習總結
20172313 2018-2019-1 《程式設計與資料結構》第五週學習總結
教材學習內容總結
- 查詢
- 查詢是這樣一個過程,即在某個專案組中尋找某一指定目標元素,或者確定該指定目標並不存在。
- 高效的查詢會使該過程所做的比較操作次數最小化。
- 通過將方法宣告成泛型,我們可以將所有的排序和查詢方法位於這個類中。但是,對於這種方式定義的Searching類,要求我們在使用查詢或排序方法時必須例項化。這對只含有方法而無其他內容的類來說是一件糟糕的事情,一種更好的解決方案是把所有方法宣告為靜態或泛型。
public classs Searching<T extends Comparable<T>> - 要建立一個泛型方法,只需在方法頭的返回型別前插入一個泛型宣告即可。
public static <T extends Comparable<T>> Boolean
LinearSearch (T[] data, int min, int max, Ttarget)- 線性查詢法:從該列表頭開始依次比較每一個值,直到找到該目標元素。
- 二分查詢法
- 二分查詢要求查詢池中的專案組都是已排序的。
- 二分查詢的每次比較都會刪除一半的可行候選項。
- 查詢演算法的比較
- 線性查詢演算法具有限行時間複雜度O(n)。因為試一次每回查詢一個元素,所以複雜度是線性的————直接與待查詢元素數目成比例。
- 二分查詢具有一個對數演算法且具有時間複雜度O(l0g2n)。二分查詢的複雜度是對數集的,這使得它對於大型查詢池非常有效率。
- 如果說對數查詢比線性查詢更有效率,那麼為什麼我們還要使用線性查詢?第一,線性查詢一般比二分查詢要簡單,因此我們程式設計和除錯起來更容易。第二,線性查詢無需花費額外成本來排序該查詢列表。在將查詢池保持為排序狀態和提高查詢效率的努力之間存在著權衡關係。
- 排序
- 排序是這樣一個過程,即基於某一標準,將某一組專案按照某個規定順序排列。
- 排序演算法通常分為兩類:順序排序: 它通常使用一對巢狀迴圈對n個元素排序,需要大約n2次比較;對數排序:它對n個元素進行排序通常需要大約nlog2n次比較。
- 選擇排序法:通過反覆地將某特定值放到它在列表中的最終已排序位置從而完成對某一列表值的排序:(1)首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置(2)再從剩餘未排序元素中繼續尋找最小(大)元素,然後放到已排序序列的末尾。(3)重複第二步,直到所有元素均排序完畢。。
- 插入排序:通過反覆地將某一特定值放到它在列表中的最終已排序位置從而完成對某一列表值的排序:(1)將第一待排序序列第一個元素看做一個有序序列,把第二個元素到最後一個元素當成是未排序序列。(2)從頭到尾依次掃描未排序序列,將掃描到的每個元素插入有序序列的適當位置。(如果待插入的元素與有序序列中的某個元素相等,則將待插入元素插入到相等元素的後面。)

- 氣泡排序法:氣泡排序法通過重複地比較相鄰元素且在必要時將他們互換,從而完成對某個列表的排序。(1)比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。(2)對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。這步做完後,最後的元素會是最大的數。(3)針對所有的元素重複以上的步驟,除了最後一個。(4)持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。
- 快速排序法:通過將列表分析,然後對著兩個分割槽進行遞迴式排序,從而完成對某個列表的排序。(1)從數列中挑出一個元素,稱為 “基準”(pivot)(2)重新排序數列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的後面(相同的數可以到任一邊)。在這個分割槽退出之後,該基準就處於數列的中間位置。這個稱為分割槽(partition)操作。(3) 遞迴地(recursive)把小於基準值元素的子數列和大於基準值元素的子數列排序。遞迴的最底部情形,是數列的大小是零或一,也就是永遠都已經被排序好了。雖然一直遞迴下去,但是這個演算法總會退出,因為在每次的迭代(iteration)中,它至少會把一個元素擺到它最後的位置去。
- 歸併排序法:通過將列表遞迴式分成兩半直至每一子列表都含有一個元素,然後將這些子列表歸併到一個排序順序中,從而完成對列表的排序。(1)申請空間,使其大小為兩個已經排序序列之和,該空間用來存放合併後的序列(2)設定兩個指標,最初位置分別為兩個已經排序序列的起始位置(3)比較兩個指標所指向的元素,選擇相對小的元素放入到合併空間,並移動指標到下一位置(4)重複步驟3直到某一指標達到序列尾(5)將另一序列剩下的所有元素直接複製到合併序列尾
- 基數排序法:是基於佇列處理,使用排列金鑰而不是直接地進行比較元素,來實現元素排序。是將陣列分到有限數量的桶子裡。每個桶子再個別排序(有可能再使用別的排序演算法或是以遞迴方式繼續使用桶排序進行排序)。桶排序是鴿巢排序的一種歸納結果。當要被排序的陣列內的數值是均勻分配的時候,桶排序使用線性時間(Θ(n))。但桶排序並不是 比較排序,他不受到 O(n log n) 下限的影響。 簡單來說,就是把資料分組,放在一個個的桶中,然後對每個桶裡面的在進行排序。
- 各種排序演算法效率比較
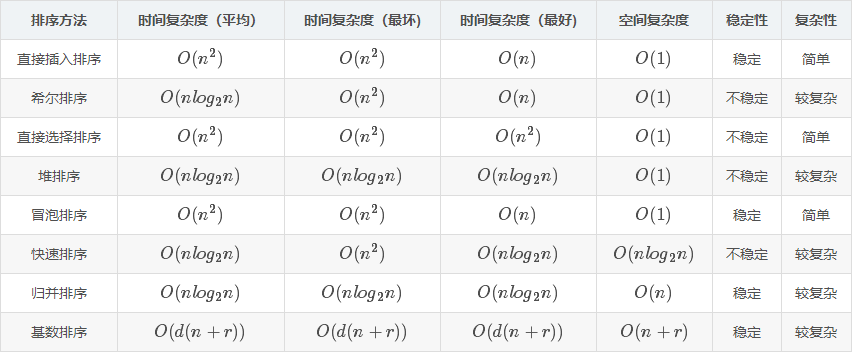
教材學習中的問題和解決過程
- 問題一:在我的理解中,氣泡排序就是比較相鄰位置的元素,根據大小將它們互換。而插入排序把特定值放到已排序的位置也需要相鄰元素的比較,那麼它們兩者的實現的區別到底在哪?
- 問題一解決方法:
| 演算法名稱 | 最差時間複雜度 | 平均時間複雜度 | 最優時間複雜度 | 空間複雜度 | 穩定性 |
|---|---|---|---|---|---|
| 氣泡排序 | O(N^2) | O(N^2) | O(N) | O(1) | 穩定 |
| 插入排序 | O(N^2) | O(N^2) | O(N) | O(1) | 穩定 |
兩者在資料上簡直一毛一樣,只考慮複雜度的話完全可以互相替代。但深究的話,還是能找出許多不同:
打個比方:這是我們今天的主角小明,他機智勇敢熱愛學習樂於助人。有一天他上體育課,排的是3號位置,老師說:同7學們請用氣泡排序的方法排好隊。小明覺得自己比2號的小紅高,所以互換位置,成為了2號。然後他覺得比1號小剛高,所以又互換位置排到了1號。老師說:小明,滾到最後去。最終他成了100號,這就是插入排序。有一天他上體育課,排的是3號位置,老師說:同學們請用氣泡排序的方法排好隊。小明覺得自己比2號的小紅高,所以互換位置,成為了2號。然後他覺得比1號小剛高,所以又互換位置排到了1號。老師說:小明,滾到最後去。最終他成了100號,這就是插入排序。
插入排序:
將無序的元素插入到有序的元素序列中,插入後仍然有序
int min;
T temp;
for(int index = 0; index < data.length-1;index++)
{
min = index;
for(int scan = index + 1; scan < data.lenth; scan ++)
if(data[scan].compareTo(data[min])<0)
min = scan;
/*8swap the values*/
temp = data[min];
data[min] = data[index];
data[index] = temp;
}
/*
舉例:從小到大排列[2,1,4,3]
第一趟排序:[1,2,4,3] 交換次數:1 比較次數:1
第二趟排序:[1,2,4,3] 交換次數:0 比較次數:1
第三趟排序:[1,2,3,4] 交換次數:1 比較次數:2
從小到大排列[4,3,2,1]
第一趟排序:[3,4,2,1] 交換次數:1 比較次數:1
第二趟排序:[2,3,4,1] 交換次數:2 比較次數:2
第三趟排序:[1,2,3,4] 交換次數:3 比較次數:3
*/氣泡排序:
比較相鄰元素,直到序列變為有序為止
int position, scan;
T temp;
for(position = data.length - 1; position >= 0; position--){
int position, scan;
T temp;
for(position = data.length - 1;position >= 0; position--){
for(scan = 0;scan <= position - 1;scan++){
if(data[scan].compareTo(data[scan+1]) > 0)
swap(data,scan, scan + 1);
}
}
}
/*
舉例:從小到大排列[2,1,4,3]
第一趟排序:[1,2,4,3] 交換次數:1 比較次數:3
第二趟排序:[1,2,4,3] 交換次數:0 比較次數:2
第三趟排序:[1,2,3,4] 交換次數:1 比較次數:1
從小到大排列[4,3,2,1]
第一趟排序:[3,2,1,4] 交換次數:3 比較次數:3
第二趟排序:[2,1,3,4] 交換次數:2 比較次數:2
第三趟排序:[1,2,3,4] 交換次數:1 比較次數:1
*/- 問題二:在快速排序法中,如果說可以將隨意一個數作為分割槽元素的話,那麼如何保證分割槽元素前後元素個數相同呢?對快速排序法不是很瞭解。
- 問題三解決方案:我對於快速排序法理解有誤。假設我們現在對“6 1 2 7 9 3 4 5 10 8”這個10個數進行排序。為了方便,就讓第一個數6作為基準數吧。接下來,需要將這個序列中所有比基準數大的數放在6的右邊,比基準數小的數放在6的左邊,:分別從初始序列“6 1 2 7 9 3 4 5 10 8”兩端開始“探測”。先從右往左找一個小於6的數,再從左往右找一個大於6的數,然後交換他們。這裡可以用兩個變數i和j,分別指向序列最左邊和最右邊。我們為這兩個變數起個好聽的名字“哨兵i”和“哨兵j”。剛開始的時候讓哨兵i指向序列的最左邊(即i=1),指向數字6。讓哨兵j指向序列的最右邊(即=10),指向數字。

首先哨兵j開始出動。因為此處設定的基準數是最左邊的數,所以需要讓哨兵j先出動,這一點非常重要(請自己想一想為什麼)。哨兵j一步一步地向左挪動(即j--),直到找到一個小於6的數停下來。接下來哨兵i再一步一步向右挪動(即i++),直到找到一個數大於6的數停下來。最後哨兵j停在了數字5面前,哨兵i停在了數字7面前。


現在交換哨兵i和哨兵j所指向的元素的值。交換之後的序列如下:
6 1 2 5 9 3 4 7 10 8
到此,第一次交換結束。接下來開始哨兵j繼續向左挪動(再友情提醒,每次必須是哨兵j先出發)。他發現了4(比基準數6要小,滿足要求)之後停了下來。哨兵i也繼續向右挪動的,他發現了9(比基準數6要大,滿足要求)之後停了下來。此時再次進行交換,交換之後的序列如下:
6 1 2 5 4 3 9 7 10 8
第二次交換結束,“探測”繼續。哨兵j繼續向左挪動,他發現了3(比基準數6要小,滿足要求)之後又停了下來。哨兵i繼續向右移動,糟啦!此時哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。說明此時“探測”結束。我們將基準數6和3進行交換。交換之後的序列如下:
3 1 2 5 4 6 9 7 10 8



到此第一輪“探測”真正結束。此時以基準數6為分界點,6左邊的數都小於等於6,6右邊的數都大於等於6。回顧一下剛才的過程,其實哨兵j的使命就是要找小於基準數的數,而哨兵i的使命就是要找大於基準數的數,直到i和j碰頭為止。
OK,解釋完畢。現在基準數6已經歸位,它正好處在序列的第6位。此時我們已經將原來的序列,以6為分界點拆分成了兩個序列,左邊的序列是“3 1 2 5 4”,右邊的序列是“9 7 10 8”。接下來還需要分別處理這兩個序列。因為6左邊和右邊的序列目前都還是很混亂的。不過不要緊,我們已經掌握了方法,接下來只要模擬剛才的方法分別處理6左邊和右邊的序列即可。
- 問題三:在問題二中提到因為此處設定的基準數是最左邊的數,所以需要讓哨兵j先出動,這一點非常重要,對這句話不是特別理解。
- 問題三解決方案:如果選取最左邊的數arr[left]作為基準數,那麼先從右邊開始可保證i,j在相遇時,相遇數是小於基準數的,交換之後temp所在位置的左邊都小於temp。但先從左邊開始,相遇數是大於基準數的,無法滿足temp左邊的數都小於它。所以進行掃描,要從基準數的對面開始,又或者選取最中間的數作為基準數就不會出現類似問題。
- 問題四:在學習基數排序法的時候,瞭解到基數排序是基於佇列處理的,並且要基於排序關鍵字,但基數排序法是如何實現的?基數和排序關鍵字又是如何選取的?
- 問題四解決方案:我覺得用理論來解釋是空泛的,舉個例子能更好的幫助理解。
例如要對大小為[1..1000]範圍內的n個整數A[1..n]排序
首先,可以把桶設為大小為10的範圍,具體而言,設集合B[1]儲存[1..10]的整數,集合B[2]儲存 (10..20]的整數,……集合B[i]儲存( (i-1)10, i10]的整數,i = 1,2,..100。總共有 100個桶。
然後,對A[1..n]從頭到尾掃描一遍,把每個A[i]放入對應的桶B[j]中。 再對這100個桶中每個桶裡的數字排序,這時可用冒泡,選擇,乃至快排,一般來說任 何排序法都可以。
最後,依次輸出每個桶裡面的數字,且每個桶中的數字從小到大輸出,這 樣就得到所有數字排好序的一個序列了。
假設有n個數字,有m個桶,如果數字是平均分佈的,則每個桶裡面平均有n/m個數字。如果對每個桶中的數字採用快速排序,那麼整個演算法的複雜度是
O(n + m * n/m*log(n/m)) = O(n + nlogn – nlogm)
從上式看出,當m接近n的時候,桶排序複雜度接近O(n)
當然,以上覆雜度的計算是基於輸入的n個數字是平均分佈這個假設的。這個假設是很強的 ,實際應用中效果並沒有這麼好。如果所有的數字都落在同一個桶中,那就退化成一般的排序了。
前面說的幾大排序演算法 ,大部分時間複雜度都是O(n2),也有部分排序演算法時間複雜度是O(nlogn)。而桶式排序卻能實現O(n)的時間複雜度。但桶排序的缺點是:
1)首先是空間複雜度比較高,需要的額外開銷大。排序有兩個陣列的空間開銷,一個存放待排序陣列,一個就是所謂的桶,比如待排序值是從0到m-1,那就需要m個桶,這個桶陣列就要至少m個空間。
2)其次待排序的元素都要在一定的範圍內等等。
程式碼除錯中的問題和解決過程
- 問題1:在做程式設計專案pp9_3的時候,不知道怎麼計算程式的執行時間。
- 問題一解決方案:
一般輸出日期時間經常會用到Date這個類:
SimpleDateFormat df = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");//設定日期格式
System.out.println(df.format(new Date()));// new Date()為獲取當前系統時間
(1)以毫秒為單位計算
static long currentTimeMillis() , 該方法返回值是從1970年1月1日凌晨到此時刻的毫秒數
long startTime=System.currentTimeMillis(); //獲取開始時間
doSomeThing(); //測試的程式碼段
long endTime=System.currentTimeMillis(); //獲取結束時間
System.out.println("程式執行時間: "+(end-start)+"ms");(2)以納秒為單位計算
long startTime=System.nanoTime(); //獲取開始時間
doSomeThing(); //測試的程式碼段
long endTime=System.nanoTime(); //獲取結束時間
System.out.println("程式執行時間: "+(end-start)+"ns");程式碼託管

上週考試錯題總結
這周沒有錯題哦~
結對及互評
- 部落格中值得學習的或問題:
- 排版精美,對教材的總結細緻,善於發現問題,對於問題研究得很細緻,解答也很周全。
- 程式碼中值得學習的或問題:
- 程式碼寫的很規範,思路很清晰,繼續加油!
點評過的同學部落格和程式碼
其他(感悟、思考等,可選)
國慶假期過去了,這周的學習效率還算可以,完成了學習任務,達到了自己預期的目標,但在看了其他同學的部落格後,還是感到自己的學習時間還是遠遠不夠,相比之下,自己的學習效率還是較低的,希望能夠在以後的學習中繼續進步!
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 第一週 | 200/200 | 1/1 | 5/20 | |
| 第二週 | 981/1181 | 1/2 | 15/20 | |
| 第三週 | 1694/2875 | 1/3 | 15/35 | |
| 第四周 | 3129/6004 | 1/4 | 15/50 | |
| 第五週 | 1294/7298 | 1/5 | 15/65 |
計劃學習時間:15小時
實際學習時間:15小時

