標題：螺旋折線

如圖p1.png所示的螺旋折線經過平面上所有整點恰好一次。
對於整點(X, Y)，我們定義它到原點的距離dis(X, Y)是從原點到(X, Y)的螺旋折線段的長度。

例如dis(0, 1)=3, dis(-2, -1)=9

給出整點座標(X, Y)，你能計算出dis(X, Y)嗎？

【輸入格式】
X和Y

對於40%的資料，-1000 <= X, Y <= 1000
對於70%的資料，-100000 <= X， Y <= 100000
對於100%的資料, -1000000000 <= X, Y <= 1000000000

【輸出格式】
輸出dis(X, Y)

【樣例輸入】
0 1

【樣例輸出】
3

資源約定：
峰值記憶體消耗（含虛擬機器） < 256M
CPU消耗 < 1000ms

請嚴格按要求輸出，不要畫蛇添足地列印類似：“請您輸入…” 的多餘內容。

注意：
main函式需要返回0;
只使用ANSI C/ANSI C++ 標準;
不要呼叫依賴於編譯環境或作業系統的特殊函式。
所有依賴的函式必須明確地在原始檔中 #include
不能通過工程設定而省略常用標頭檔案。

提交程式時，注意選擇所期望的語言型別和編譯器型別。

/*
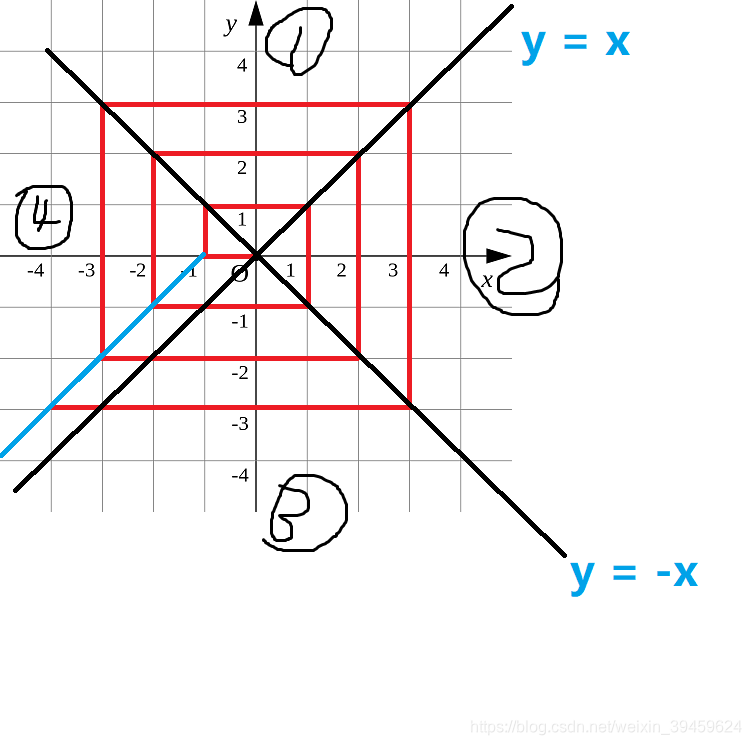
開始的時候，想法就是一個點一個點的遍歷，但是後面發現數據給的很大，這樣遍歷的話，直接就炸了（超時）。
後面就想能不能直接進行計算，確實也找到直接計算的方法，如上圖所示，將整個空間用函式y = x和y = -x 分為四個空間，分別討論即可。
當時是發現了在第一象限中 y = x 上的點，對應的位置是 4 16 36 等，第四象限中藍色那條線為 1 9 25，看到這裡就想到了與平方有關係，最後還真的與他們有關係，具體的看程式碼吧。 
注意int溢位，需要使用 long long
*/
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
int main(){
    LL x, y;
    LL temp;
    while(cin >> x >> y){	//測試的時候為了不用每次測試的時候都執行程式，而設定的迴圈
	    if(y >= x && y > 0 && y >= -x){	//在第一部分中的點的座標與結果的關係
	        temp = (2*max(x,y));
	        cout << temp*temp - abs(x-y) << endl;
	    }else if(x >= y && x > 0 && y >= -x){	//在第二部分中的點的座標與結果的關係
	        temp = (2*max(x,y));
	        cout << temp*temp + abs(x-y) << endl;
	    }else if(y > x && x < 0 && y <= -x){	//在第四部分中的點的座標與結果的關係
	        temp = (2*max(abs(x),abs(y))-1);
	        cout << temp*temp + abs(x-y) - 1 << endl;;
	    }else if(x >= y && y < 0 && y <= -x){	//在第三部分中的點的座標與結果的關係
	        temp = 2*max(abs(x), abs(y))+1;
	        cout << temp*temp - abs(x-y) - 1 << endl;
	    }
    }
    return 0;
}
 

僅僅只是自己的看法，因為沒有完整的測試資料，小資料測試基本沒有問題，如果有更好的方法或者程式有誤，請留言