20172301 《Java軟體結構與資料結構》實驗二報告
20172301 《Java軟體結構與資料結構》實驗二報告
課程:《Java軟體結構與資料結構》
班級: 1723
姓名: 郭愷
學號:20172301
實驗教師:王志強老師
實驗日期:2018年11月20日
必修/選修: 必修
一.實驗內容
實驗1
實驗2
實驗3

實驗4

實驗5
實驗6

二.實驗過程及結果
實驗1
LinkedBinaryTree因為是之前的程式專案,所以實現起來很容易。
getRight()方法,首先在LinkedBinaryTree類裡面宣告一個全域性變數
protected LinkedBinaryTree<T> left,right;
然後在建構函式裡,新增下面兩行程式碼。
// 建立以指定元素為根元素的二叉樹,把樹作為它的左子樹和右子樹 public LinkedBinaryTree(T element, LinkedBinaryTree<T> left, LinkedBinaryTree<T> right) { root = new BinaryTreeNode<T>(element); root.setLeft(left.root); root.setRight(right.root); this.left = left; this.right = right; }
然後直接返回right即可。
// 返回此樹的根的右子樹。
public LinkedBinaryTree<T> getRight()
{
return right;
}contains方法基於私有方法findAgain實現。只需要判斷在樹裡能否找到目標元素即可。
public boolean contains(T targetElement)
{
return findAgain(targetElement, root) != null;
}toString方法,這裡為了讓輸出是一個樹型,我用了之前ExpressionTree的printTree方法。同樣,toString方法可以考慮使用四種遍歷方式。preorder方法和postorder方法,實現理念和書上給的中序遍歷一樣。只需要調整一下左右孩子還有結點的順序。
// 執行遞迴先序遍歷。
protected void preOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList)
{
if (node != null)
{
tempList.addToRear(node.getElement());
preOrder(node.getLeft(), tempList);
preOrder(node.getRight(), tempList);
}
}// 執行遞迴後序遍歷。
protected void postOrder(BinaryTreeNode<T> node,
ArrayUnorderedList<T> tempList)
{
if (node != null)
{
postOrder(node.getLeft(), tempList);
postOrder(node.getRight(), tempList);
tempList.addToRear(node.getElement());
}
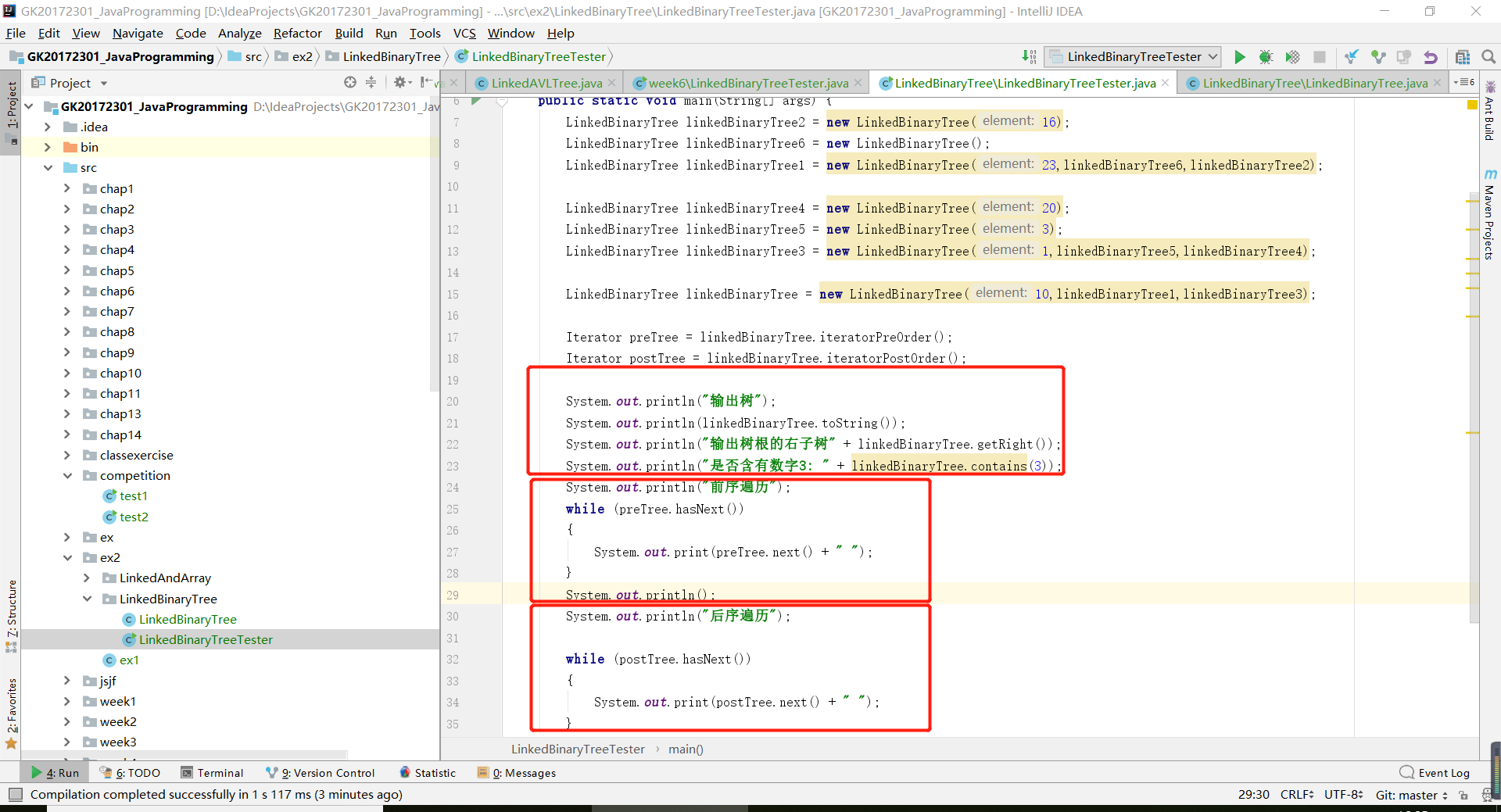
}- 接下來是測試類和測試結果

實驗2
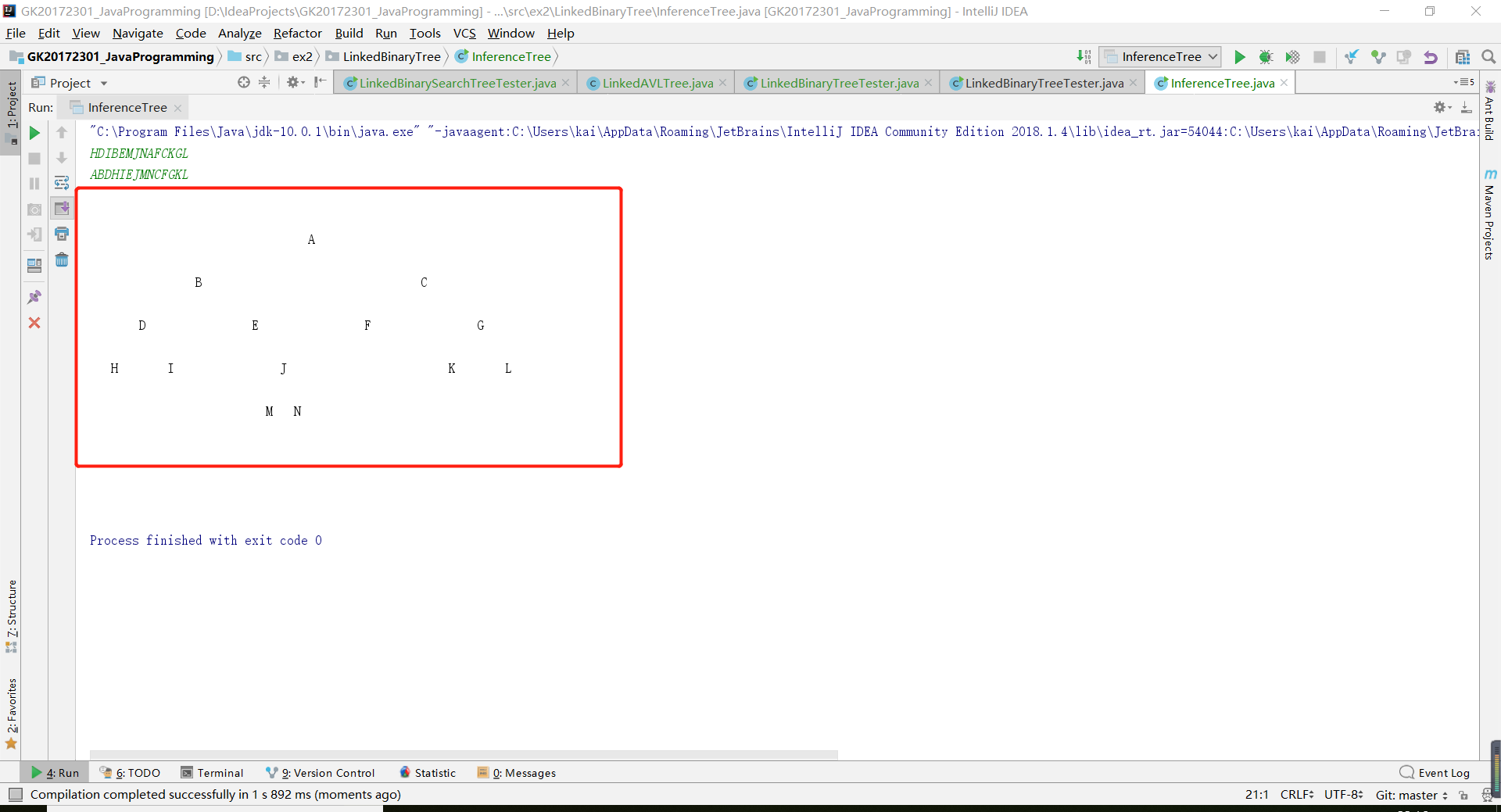
- 根據之前上課講的方法,我們首先要確定如何推斷出根和根的左右孩子。例如題目中的兩個字串,中序
HDIBEMJNAFCKGL和先序ABDHIEJMNCFGKL。
中序分左右,先後序定根。
這裡,我一開始是沒有什麼思路的,因為我自己推導先序和中序構造樹的時候,並沒有系統的方法。所以我也在網上找到了一些資料,如何有步驟的去分析先序和中序。 - 會分為以下幾個步驟:
- 確定整棵二叉樹的根節點即先序遍歷中的第一個元素root
- 確定root在中序遍歷元素的位置,root左邊的元素為二叉樹的左子樹元素Lchild,右邊為右子樹元素Rchild
- 在先序遍歷中找到最先出現Lchild中元素的那個元素,為Lchild的根節點——root的左孩子節點,同理找出Rchild的根節點——root的右孩子節點
- 重複2,3步驟直至二叉樹構建完成;
- 那麼,我們沿著這個思路,就能根據先序得知
A是樹的根結點。那麼根據中序得知A的左邊是左子樹,A的右邊是右子樹。 - 同理,根據先序
B即是左子樹的根,根據中序得知B的左邊是左子樹的左孩子,B的右邊是左子樹的右孩子。 - 依次往下,知道左右孩子為空的時候。這時候即可返回以
A為根的樹。 - 所以,運用遞迴,分別遞迴實現左子樹和右子樹。
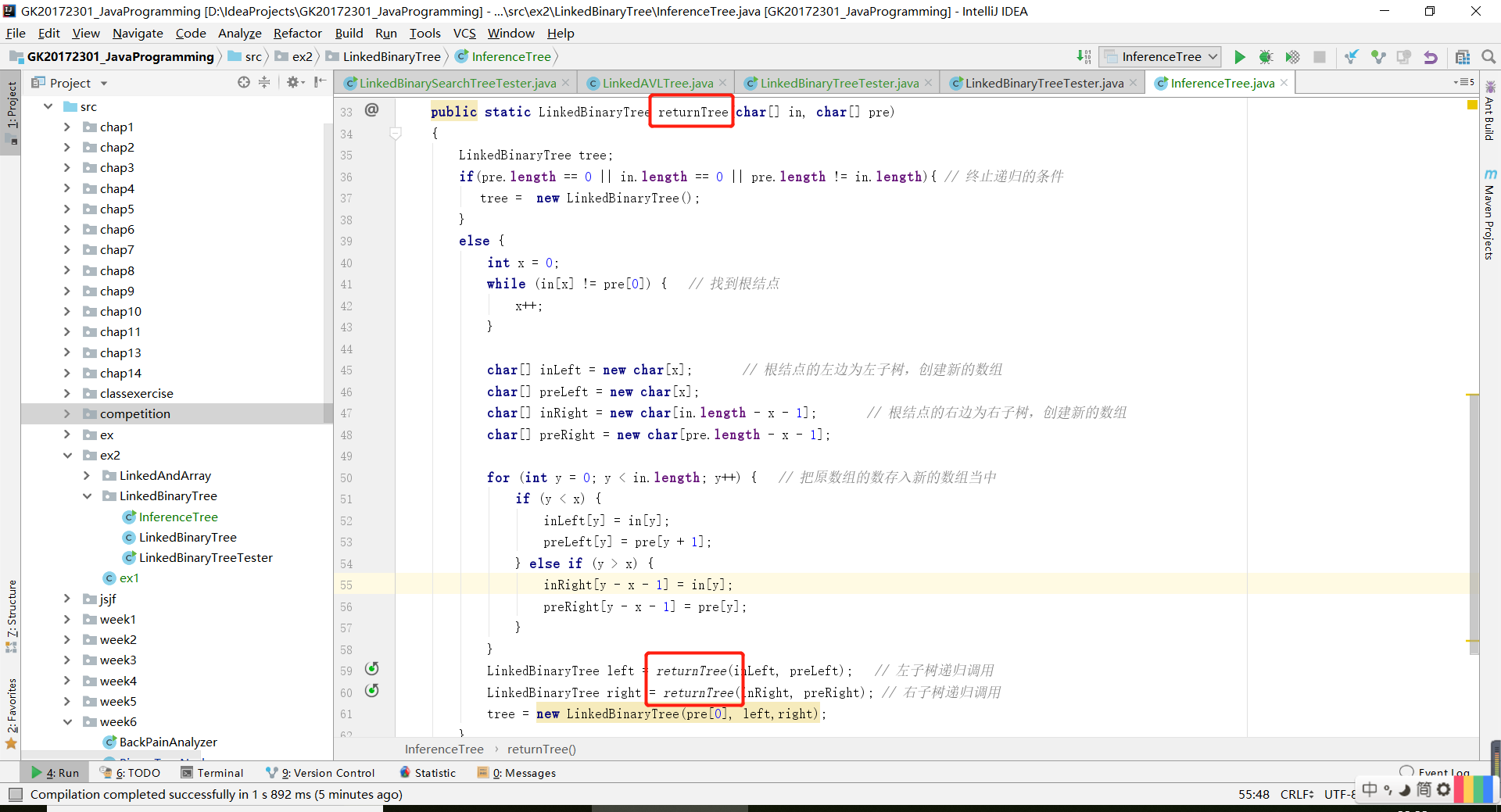
- 最後,以
A為根結點和遞迴實現的左右子樹,建立一個新樹。 - 接下來是測試程式碼和程式碼結果。
實驗3
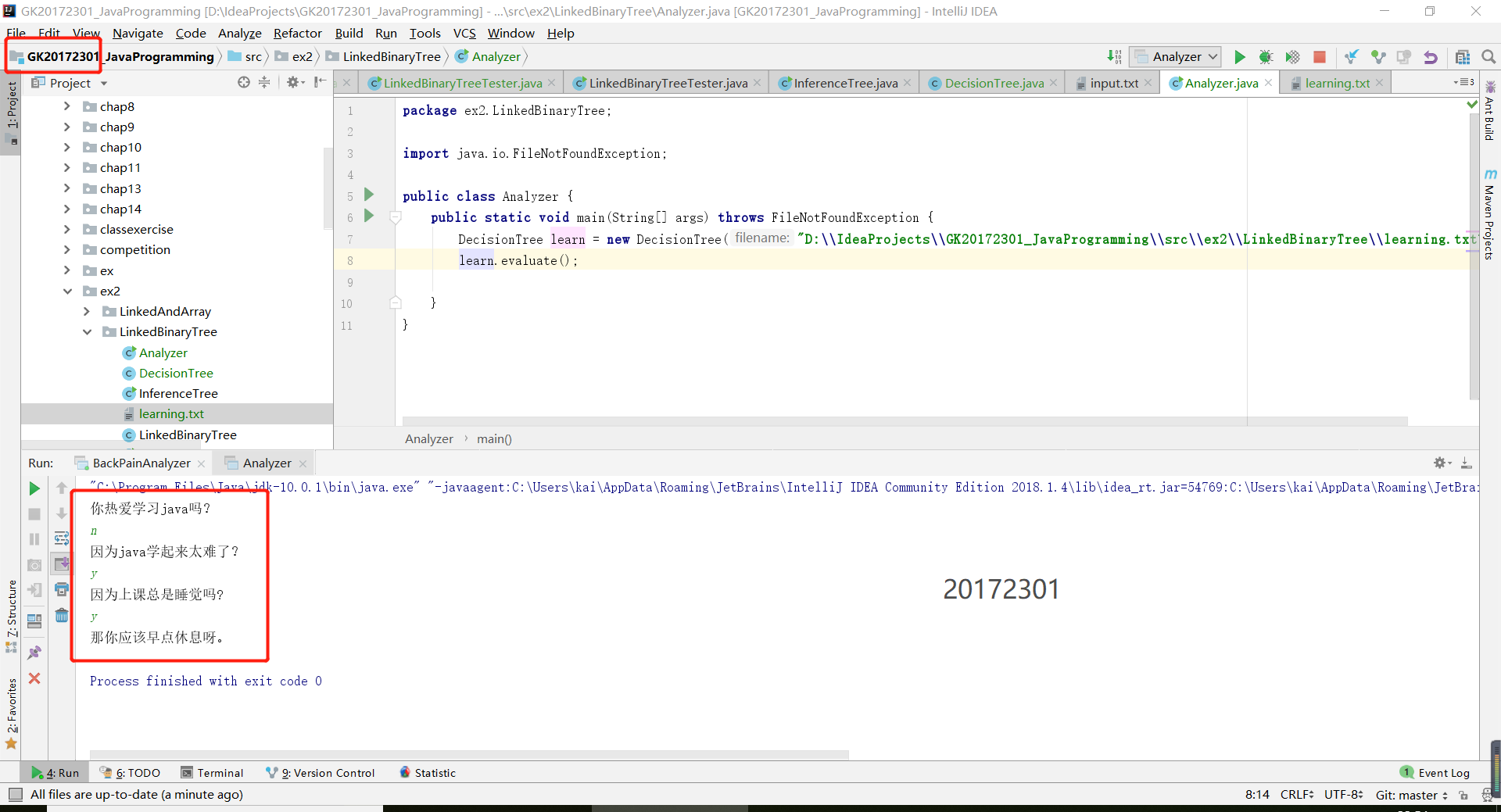
- 決策樹相對來說比較簡單,因為書上的背部疼痛診斷器給出了一個決策樹的流程。我們只需要設計一棵新的決策樹即可。
- 檔案裡包含著一些數字,是因為第一個數字是表明你有幾個語句,然後下面的是為了構建左右子樹。
- 測試程式碼和結果
實驗4
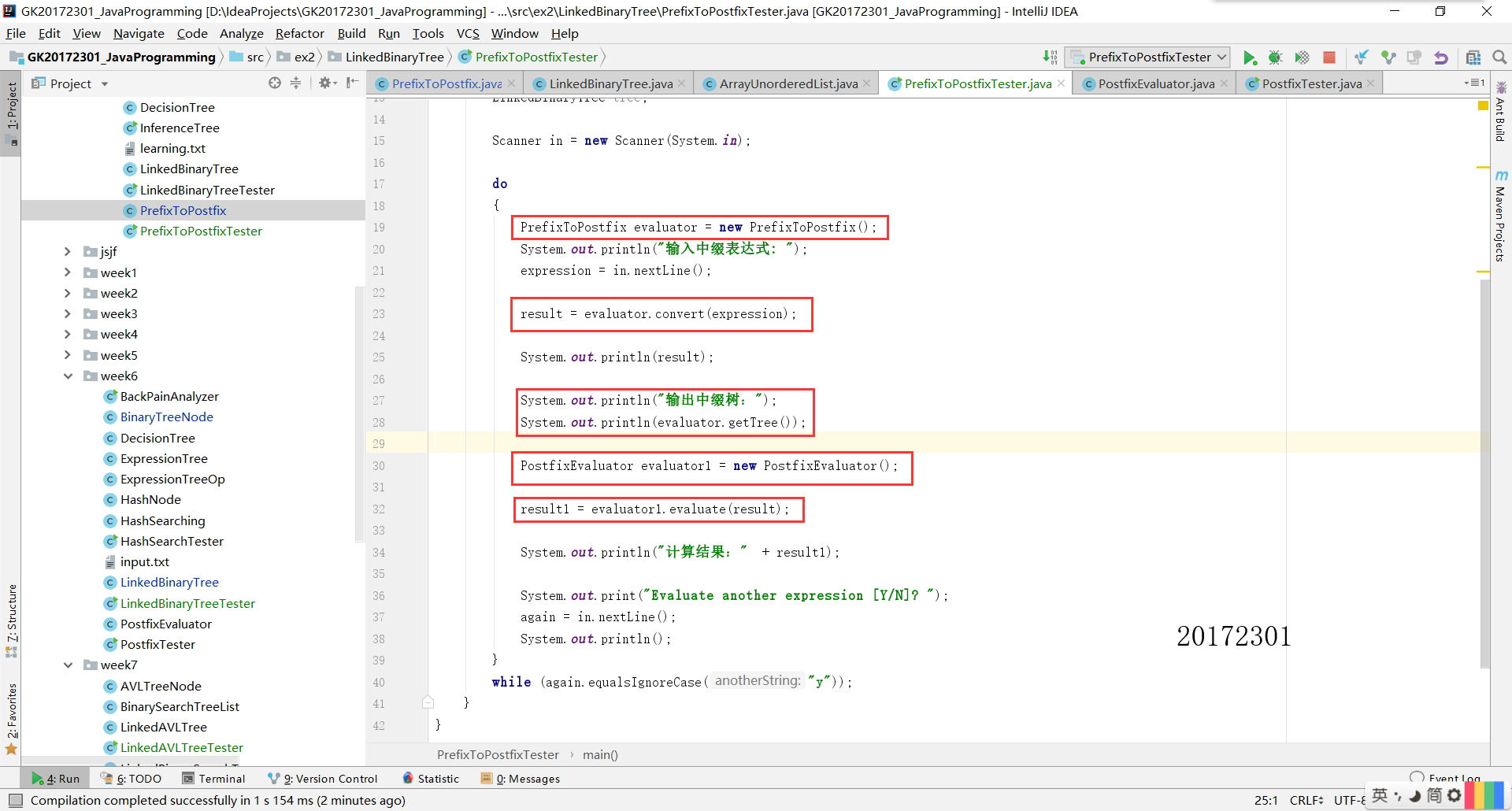
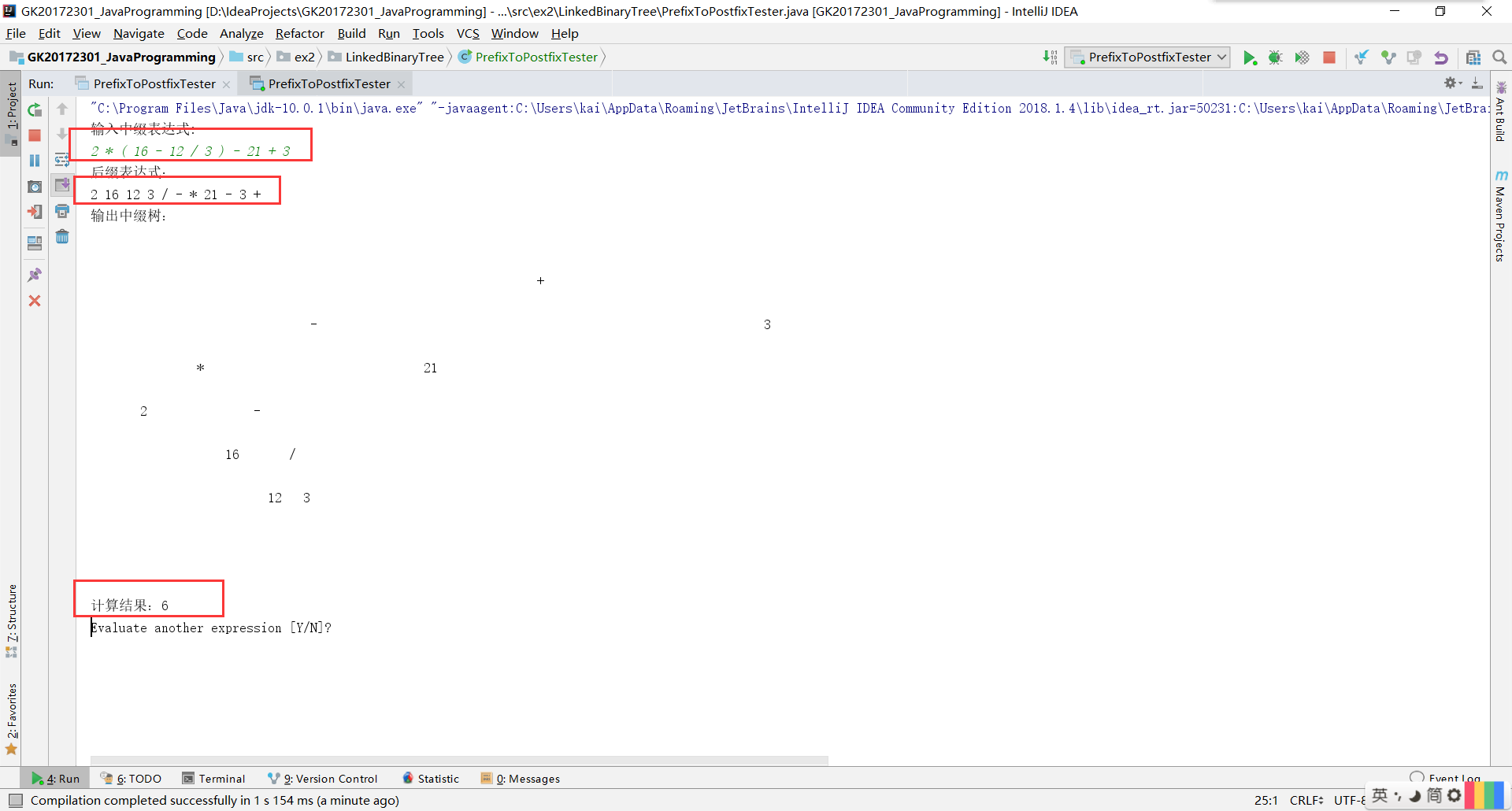
- 實驗四是輸入中綴表示式,使用樹將中綴表示式轉換為字尾表示式,並輸出字尾表示式和計算結果。書上有一個
ExpresstionTree是關於字尾表示式計算的一個樹。 - 這個我一開始也沒有什麼思路,但是實際上也就是一個表示式樹,符號作為根,然後運算元是他的左右子樹。 我參考書上字尾計算的例子,運用一個表示式式棧,注意:這個棧裡面存放的是樹型的。為了實現的方便,我直接存放的是二叉樹,並沒有用表示式樹。然後還有一個符號棧。這裡還需要考慮一個優先順序的問題,** 優先順序高的要在底層。**
- 具體的實現思路和判斷條件和上學期的差不多,我並沒有改動多少,主要注意的就是樹的存放和符號左右兩個運算元的順序。我便不多贅述。括號問題將在問題中詳細說明。
- 程式碼測試和結果
實驗5
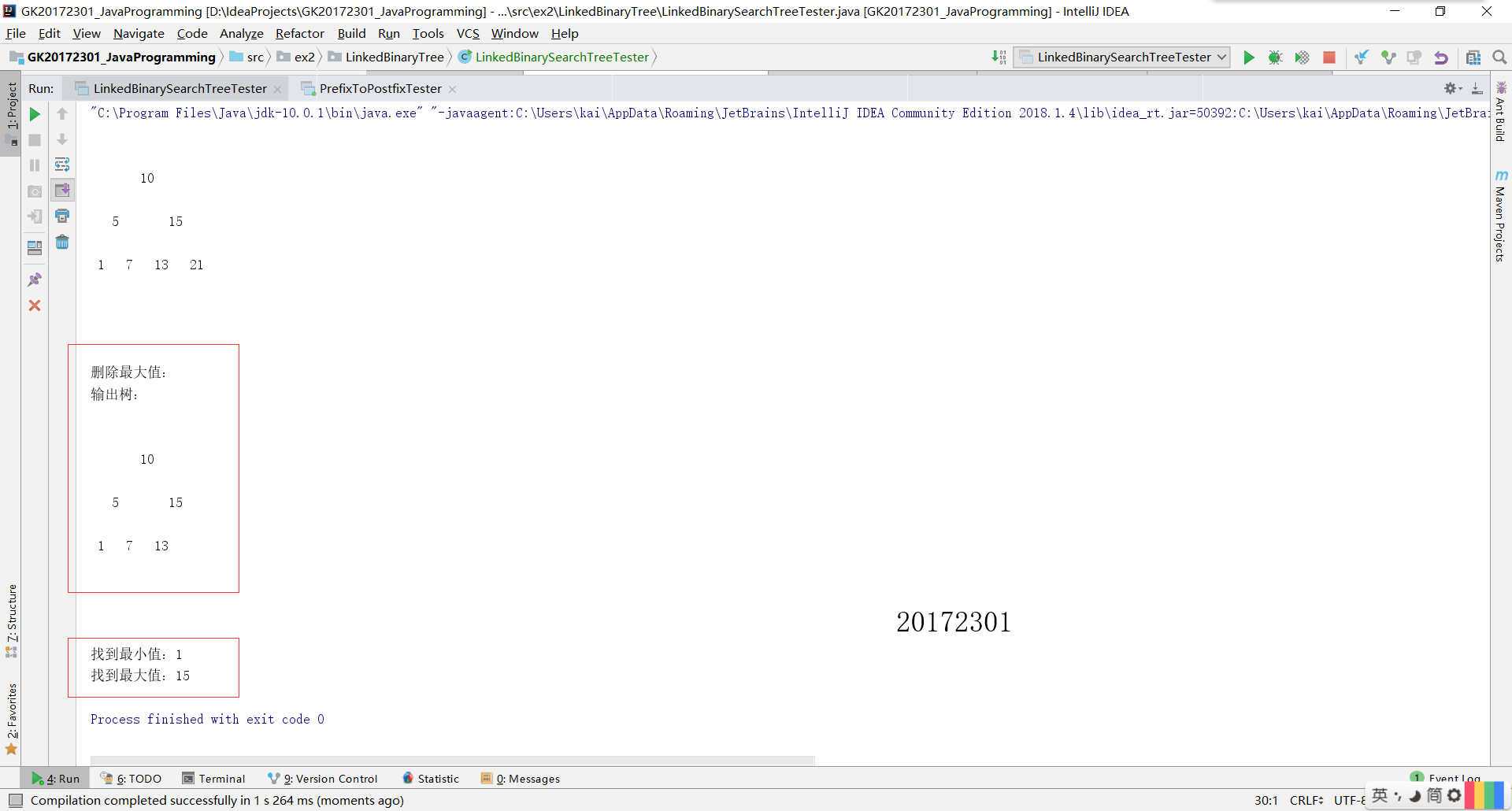
- 實驗五是之前的課後專案,已經實現過。二叉查詢樹的特點是,左子樹的最左結點是最小值,樹的右子樹的最右結點是最大值,。所以,實現
findMin和findMax只要分別查詢最左結點和最右結點即可。 - 測試程式碼和結果

實驗6
在看原始碼之前,我覺得有必要學習一下如何去系統的看程式原始碼。這裡做一些摘錄:
第一,找准入口出口,不要直接跳進去看,任何程式碼都有觸發點,無論是http request,還是伺服器自動啟動,還是main函式,還是其他的,先從入口開始。
第二,手邊一支筆一張紙,除非你是Jeff,否則你不會記得那麼多跳轉的。一個跳轉就寫下來函式/方法名和引數,讀完一遍,就有了一個sequence diagram雛形 。
第三,私有方法掠過,只要記住輸入輸出即可,無需看具體實現
紅黑樹遵循以下五點性質:
性質1 結點是紅色或黑色。
性質2 根結點是黑色。
性質3 每個葉子結點(NIL結點,空結點)是黑色的。
性質4 每個紅色結點的兩個子結點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色結點)
性質5 從任一結點到其每個葉子結點的所有路徑都包含相同數目的黑色結點。- TreeMap
- 首先看一下
TreeMap宣告
public class TreeMap<K,V> extends AbstractMap<K,V> implements NavigableMap<K,V>, Cloneable, java.io.Serializable {- 構造方法
public TreeMap() { comparator = null; }無參構造方法,不指定比較器,排序的實現要依賴
key.compareTo()方法,因此key必須實現Comparable介面,並覆寫其中的compareTo方法。
public TreeMap(Comparator<? super K> comparator) { this.comparator = comparator; }
採用帶比較器的構造方法,排序依賴該比較器,key可以不用實現Comparable介面。
public TreeMap(Map<? extends K, ? extends V> m) { comparator = null; putAll(m); }
構造方法同樣不指定比較器,呼叫putAll方法將Map中的所有元素加入到TreeMap中。
public TreeMap(SortedMap<K, ? extends V> m) { comparator = m.comparator(); try { buildFromSorted(m.size(), m.entrySet().iterator(), null, null); } catch (java.io.IOException | ClassNotFoundException cannotHappen) { } }
將比較器指定為m的比較器,而後呼叫buildFromSorted方法,將SortedMap中的元素插入到TreeMap中,根據SortedMap建立的TreeMap,將SortedMap中對應的元素新增到TreeMap中。- put操作
public V put(K key, V value) { //得到紅黑樹根結點 Entry<K,V> t = root; if (t == null) { compare(key, key); // type (and possibly null) check // 如果樹為空,新建紅黑樹根結點 root = new Entry<>(key, value, null); size = 1; modCount++; return null; } //如果Map不為空,找到插入新節點的父節點 int cmp; Entry<K,V> parent; Comparator<? super K> cpr = comparator; // 如果比較器不為空 if (cpr != null) { do { // 使用 parent 上次迴圈後的 t 所引用的 Entry parent = t; // 拿新插入的key和t的key進行比較 cmp = cpr.compare(key, t.key); // 如果新插入的key小於t的key,t等於t的左結點 if (cmp < 0) t = t.left; // 如果新插入的key大於t的key,t等於t的右結點 else if (cmp > 0) t = t.right; else // 如果兩個key相等,新value覆蓋原有的value,並返回原有的value return t.setValue(value); } while (t != null); } // 沒有提供比較器 else { if (key == null) throw new NullPointerException(); @SuppressWarnings("unchecked") Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } // 將新插入的結點作為parent結點的子結點 Entry<K,V> e = new Entry<>(key, value, parent); // 作為左孩子 if (cmp < 0) parent.left = e; // 作為右孩子 else parent.right = e; // 修復紅黑樹 fixAfterInsertion(e); size++; modCount++; return null; }- 每當程式希望新增新結點時,總是從樹的跟結點開始比較,即將根結點當成當前結點。
- 如果新增結點大於當前結點且當前結點的右子結點存在,則以右子結點作為當前結點;
- 如果新增結點小於當前結點且當前結點的左子結點存在,則以左子結點作為當前結點;
- 如果新增結點等於當前結點,則用新增結點覆蓋當前結點,並結束迴圈,直到找到某個結點的左、右子結點不存在
- 將新增結點新增為該結點的子結點。如果新結點比該結點大,則新增其為右子結點;如果新結點比該結點小,則新增其為左子結點。
- 首先看一下
- HashMap
- 首先看一下
HashMap類的宣告,可以瞭解他繼承了什麼類和實現了哪些介面。
public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable {<K,V>應該表示的是一種對映關係。
HashMap 的例項有兩個引數影響其效能:初始容量 和載入因子。
容量是雜湊表中桶的數量,初始容量只是雜湊表在建立時的容量。
載入因子是雜湊表在其容量自動增加之前可以達到多滿的一種尺度。當雜湊表中的條目數超出了載入因子與當前容量的乘積時,則要對該雜湊表進行 rehash 操作(即重建內部資料結構),從而雜湊表將具有大約兩倍的桶數。這裡有兩個比較重要的變數,容量和載入因子。容量的值是2的n次冪,載入因子預設為0.75。

這裡載入因子為什麼預設是0.75呢?
通常,預設載入因子 (0.75) 在時間和空間成本上尋求一種折衷。載入因子過高雖然減少了空間開銷,但同時也增加了查詢成本(在大多數 HashMap 類的操作中,包括 get 和 put 操作,都反映了這一點)。在設定初始容量時應該考慮到對映中所需的條目數及其載入因子,以便最大限度地減少 rehash 操作次數。
如果初始容量大於最大條目數除以載入因子,則不會發生 rehash 操作。
這裡的rehash操作,我覺得類似於陣列的擴容。載入因子就是表示陣列連結串列填滿的程度。
因此,必須在 "衝突的機會"與"空間利用率"之間尋找一種平衡與折衷.
載入因子越大,填滿的元素越多,空間利用率高了,但衝突的機會加大了.連結串列長度會越來越長,查詢效率降低。
載入因子越小,填滿的元素越少,衝突的機會減小了,但空間浪費多了.表中的資料將過於稀疏,很多空間還沒用,就開始擴容了。
如果機器記憶體足夠,並且想要提高查詢速度的話可以將載入因子設定小一點;相反如果機器記憶體緊張,並且對查詢速度沒有什麼要求的話可以將載入因子設定大一點。不過一般我們都不用去設定它,讓它取預設值0.75就好了。
- 建構函式:
// 初始容量(必須是2的n次冪),負載因子 public HashMap(int initialCapacity, float loadFactor) { if (initialCapacity < 0) throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; if (loadFactor <= 0 || Float.isNaN(loadFactor)) throw new IllegalArgumentException("Illegal load factor: " + loadFactor); this.loadFactor = loadFactor; this.threshold = tableSizeFor(initialCapacity); }- 我發現其中還有一個指標類,
HashMap使用了陣列,連結串列和紅黑樹,多種實現。
static class Node<K,V> implements Map.Entry<K,V> { final int hash; final K key; V value; Node<K,V> next; Node(int hash, K key, V value, Node<K,V> next) { this.hash = hash; // 雜湊值 this.key = key; // 鍵 this.value = value; // 值 this.next = next; // 下一個 } public final K getKey() { return key; } public final V getValue() { return value; } public final String toString() { return key + "=" + value; } public final int hashCode() { return Objects.hashCode(key) ^ Objects.hashCode(value); } public final V setValue(V newValue) { V oldValue = value; value = newValue; return oldValue; } // 判斷兩個Node是否相等 // 若兩個Node的“key”和“value”都相等,則返回true。 // 否則,返回false public final boolean equals(Object o) { if (o == this) return true; if (o instanceof Map.Entry) { Map.Entry<?,?> e = (Map.Entry<?,?>)o; if (Objects.equals(key, e.getKey()) && Objects.equals(value, e.getValue())) return true; } return false; } }next,是用來處理衝突的。HashMap本來就是一個數組,如果陣列中某一個索引發生了衝突,那麼就會形成連結串列。而連結串列到一定程度的時候,就會形成紅黑樹。put操作
public V put(K key, V value) { return putVal(hash(key), key, value, false, true); } final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0) // resize()方法是重新調整HashMap的大小 n = (tab = resize()).length; // 若不為null,計算該key的雜湊值,然後將其新增到該雜湊值對應的連結串列中 if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); else { Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; //如果是紅黑樹結點 else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); else { for (int binCount = 0; ; ++binCount) { if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st treeifyBin(tab, hash); break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) resize(); afterNodeInsertion(evict); return null; }- 儘管明白一些基本操作,但還是沒有理解大多數程式碼。
- 首先看一下
三. 實驗過程中遇到的問題和解決過程
問題1:實驗二基於(中序,先序)序列構造唯一一棵二㕚樹的功能,出現了
ArrayIndexOutOfBoundsException異常,簡單來說就是陣列為空。
如圖

- 問題1解決方案:
- 首先,找到問題出現的行數,然後設定斷點進行除錯。
- 根據我以上實驗二的思路,我根據先序判斷出來的根結點,把中序分成了兩個陣列,分別是中序左子樹和中序右子樹,同理,把先序也分成兩個陣列,分別是先序左子樹和先序右子樹。
根據除錯發現,在新建了子樹的中序和先序陣列之後,我並沒有把原來陣列的值匯入到新的陣列當中。所以導致執行時丟擲了陣列空的異常。
如圖

- 那我只需要使用一個迴圈遍歷原陣列的操作,把元素賦值進新的陣列。即,以根結點為分界線,分別存入左右子樹當中。小於根結點對應索引的元素全在左子樹,大於根結點的全在右子樹。
for (int y = 0; y < in.length; y++) { // 把原陣列的數存入新的陣列當中 if (y < x) { inLeft[y] = in[y]; preLeft[y] = pre[y + 1]; } else if (y > x) { inRight[y - x - 1] = in[y]; preRight[y - x - 1] = pre[y]; } } 問題2:實驗四樹的輸出格式不對,從而導致字尾表示式輸出格式不正確。
如圖

- 問題2解決方案:
- 實現二叉樹中綴轉字尾之後,卻發現後序遍歷輸出樹的時候出來的字尾表示式格式不對。
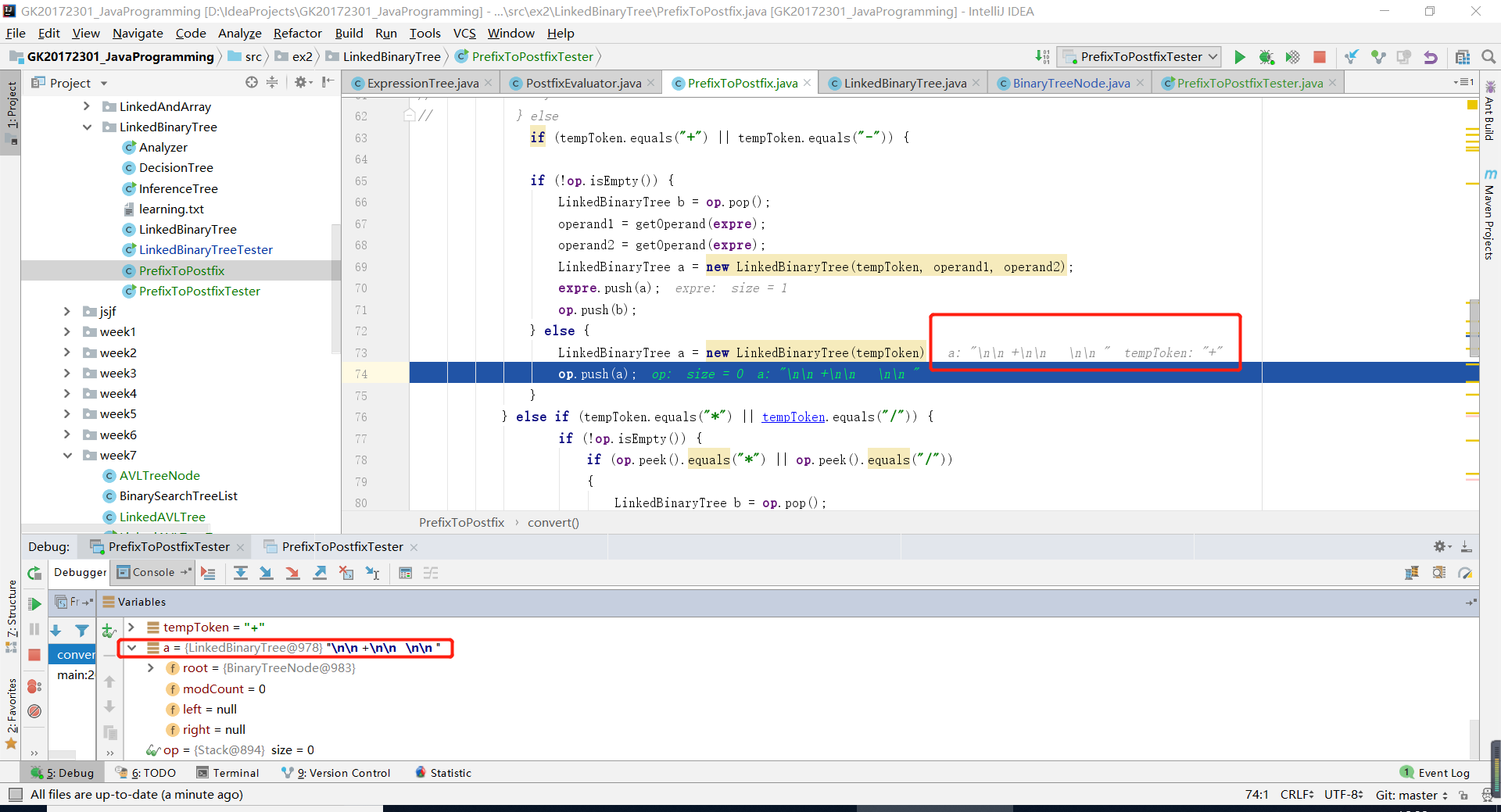
同樣是經過除錯發現,在符號入棧的時候,轉化為
LinkedBinaryTree型別儲存的時候,並以LinkedBinaryTree型別為根結點的時候,會根據其toString方法,變成,\n\n + \n\n \n\n,所以輸出樹的時候前面會多出很多行。
如圖
我的解決辦法是,把運算元棧改成
String型別的,以String型別的符號作為根結點,這樣,結果可以正常輸出。
如圖
問題3: 實驗四中綴轉字尾的括號問題。
- 問題3解決方案:
- 一開始我的括號問題想得很複雜,後來譚鑫同學告訴我,括號裡其實也是一個表示式,只要遞迴呼叫一下就可以了。確實是,如果把括號裡面的看成一個表示式,那麼就和正常的沒有括號的是一樣的啦。
- 但是後來我還是完成了自己寫的非遞迴實現,儘管程式碼可能有些複雜,但是條例還是清晰的,並且程式碼判斷條件也是不缺少的。
// 處理括號 if (tempToken.equals("(")) { op.push(tempToken); tempToken = stringTokenizer.nextToken(); while (!tempToken.equals(")")) { if (tempToken.equals("+") || tempToken.equals("-")) { if (!op.isEmpty()) { // 棧不空,判斷“(” if (op.peek().equals("(")) op.push(tempToken); else { String b = op.pop(); operand1 = getOperand(expre); operand2 = getOperand(expre); LinkedBinaryTree a = new LinkedBinaryTree(b, operand2, operand1); expre.push(a); op.push(tempToken); } } else { // 棧為空,運算子入棧 op.push(tempToken); } } else if (tempToken.equals("*") || tempToken.equals("/")) { if (!op.isEmpty()) { if (op.peek().equals("*") || op.peek().equals("/")) { String b = op.pop(); operand1 = getOperand(expre); operand2 = getOperand(expre); LinkedBinaryTree a = new LinkedBinaryTree(b, operand2, operand1); expre.push(a); op.push(tempToken); } else { op.push(tempToken); } } } else { // 運算元入棧 LinkedBinaryTree a = new LinkedBinaryTree(tempToken); expre.push(a); } tempToken = stringTokenizer.nextToken(); } while (true) { String b = op.pop(); if (!b.equals("(")) { operand1 = getOperand(expre); operand2 = getOperand(expre); LinkedBinaryTree a = new LinkedBinaryTree(b, operand2, operand1); expre.push(a); } else { // 終止迴圈 break; } } }- 這裡我用了兩個while迴圈,
第一個while迴圈 ,就是分別把符號入到符號棧裡,把表達樹入到表示式棧裡。如果壓入棧的操作符優先順序大於等於棧頂的符號,那麼就會彈出棧頂的符號,並且以彈出的符號為根和表示式樹彈出的兩個樹,形成一個新的樹,再存放到表示式棧裡。
第二個while迴圈 ,是把棧裡面括號裡面的樹和操作符全部彈出,此時棧裡面剩下的應該都是優先順序相等的,所以我們只需要把括號裡的形成一棵樹就可以了。 - 總體來說確實相對於遞迴來說較為複雜,以後還是應該考慮程式碼的優化和完整性,不能以實現目的為目的。
其他(感悟、思考等)
- 這周實驗花費了較多的時間。雖然說有些專案是之前的作業並且完成了實現。但是對於實驗二和實驗四沒有很清晰系統的思路,導致花費了太多時間去設計。還是強調程式碼的全域性性和前瞻性。比如說實驗四,括號的實現如果用遞迴來理解的話確實有事半功倍的效果。可是我卻把自己的思維侷限在了多個判斷條件上面。儘管實現了,但是從程式碼複雜性來說是不夠完美的。同樣的,對於HashMap和TreeMap也只是瞭解到了一些皮毛,但是,我們可以從其原始碼上發現自己設計實現程式碼時所缺少的東西,才能有所收穫。程式碼可能相似,但思想不會。
