20172327 2018-2019-1 《程式設計與資料結構》實驗二:樹實驗報告
阿新 • • 發佈:2018-11-11
20172327 2018-2019-1 《程式設計與資料結構》實驗二:樹實驗報告
- 課程:《Java軟體結構與資料結構》
- 班級:201723
- 姓名:馬瑞蕃
- 學號:20172327
- 實驗教師:王志強
- 實驗日期:2018年11月7日-2018年11月11日
- 必修/選修:必修
一、實驗內容:
實驗二 樹-1-實現二叉樹
- 參考教材p212,完成鏈樹LinkedBinaryTree的實現(getRight,contains,toString,preorder,postorder)
用JUnit或自己編寫驅動類對自己實現的LinkedBinaryTree進行測試
實驗二 樹-2-中序先序序列構造二叉樹
1.基於LinkedBinaryTree,實現基於(中序,先序)序列構造唯一一棵二㕚樹的功能,
2.給出中序HDIBEMJNAFCKGL和後序ABDHIEJMNCFGKL,構造出附圖中的樹
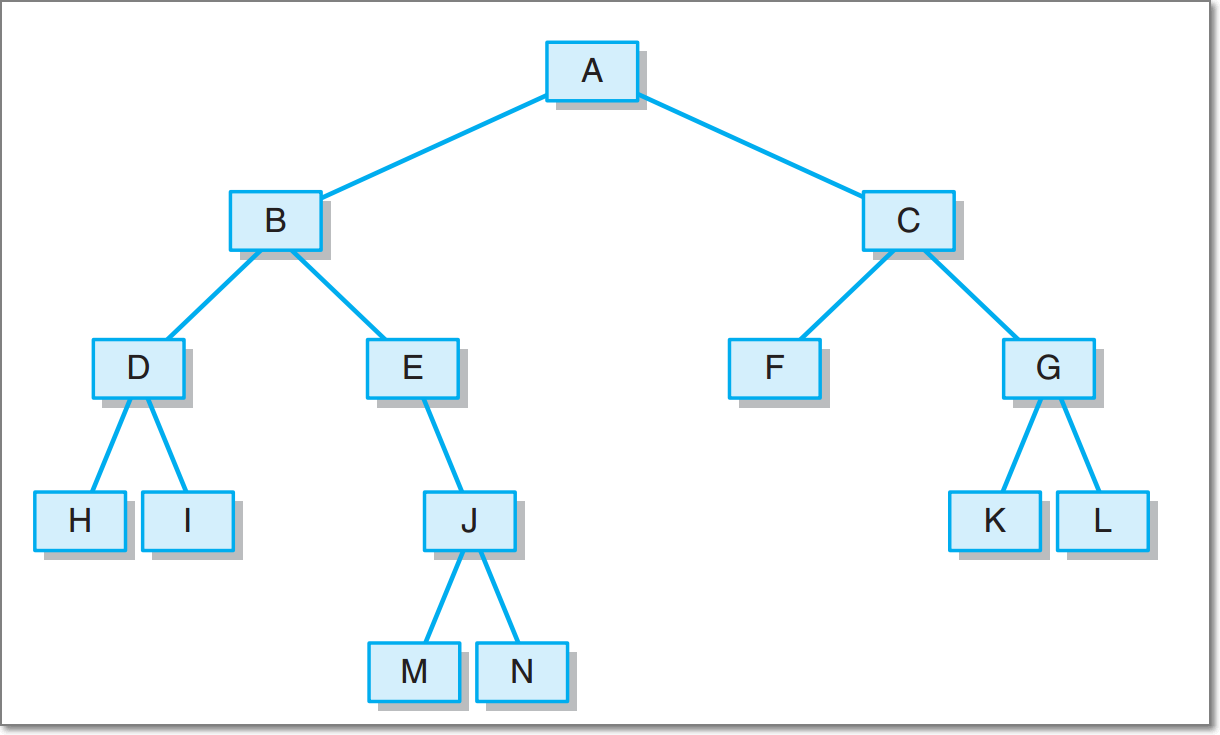
3.用JUnit或自己編寫驅動類對自己實現的功能進行測試
實驗二 樹-3-決策樹
- 1.自己設計並實現一顆決策樹
實驗二 樹-4-表示式樹
- 1.輸入中綴表示式,使用樹將中綴表示式轉換為字尾表示式,並輸出字尾表示式和計算結果(如果沒有用樹,則為0分)
實驗二 樹-5-二叉查詢樹
- 1.完成PP11.3
實驗二 樹-6-紅黑樹分析
- 參考http://www.cnblogs.com/rocedu/p/7483915.html對Java中的紅黑樹(TreeMap,HashMap)進行原始碼分析,並在實驗報告中體現分析結果。
(C:\Program Files\Java\jdk-11.0.1\lib\src\java.base\java\util)
二、實驗過程及結果:
樹-1-實現二叉樹
- 要實現 LinkedBinaryTree 中的方法,首先要將結點類 BinaryTreeNode 補充完整。在結點類中,需要補充先序遍歷和後序遍歷的函式,由於這裡用到了迭代器和遞迴的思路,所以直接參考中序遍歷給出的函式即可:
//為樹的中序遍歷返回一個迭代器 public Iterator<T> iteratorInOrder() { ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>(); inOrder(root, tempList); return new TreeIterator(tempList.iterator()); } protected void inOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) { if (node != null) { inOrder(node.getLeft(), tempList); tempList.addToRear(node.getElement()); inOrder(node.getRight(), tempList); } }
- 整左子樹、右子樹和根的訪問順序以及對應方法即可實現另外兩種函式:
//為樹的前序遍歷返回一個迭代器
public Iterator<T> iteratorPreOrder() {
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
preOrder(root, tempList);
return new TreeIterator(tempList.iterator());
}
private void preOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
if (node != null) {
tempList.addToRear(node.getElement());
inOrder(node.getLeft(), tempList);
inOrder(node.getRight(), tempList);
}
}
@Override
//為樹的後序遍歷返回一個迭代器
public Iterator<T> iteratorPostOrder() {
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
postOrder(root, tempList);
return new TreeIterator(tempList.iterator());
}
private void postOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
if (node != null) {
inOrder(node.getLeft(), tempList);
inOrder(node.getRight(), tempList);
tempList.addToRear(node.getElement());
}
}實現了結點類之後,對應地去實現方法類 LinkedBinaryTree,方法類中需要補充的函式有:getRight,contains,isEmpty,toString,preorder,postorder.
- getRight 方法可以參考給出的 getLeft 方法:
//返回結點的左側子結點
public LinkedBinaryTree<T> getLeft() {
return left;
}
//返回結點的右側子結點
public LinkedBinaryTree<T> getRight() {
return right;
}- contains 方法我主要考慮了根為空、和檢測元素為空的情況,並對此做出條件判斷即可:(如果根為空則會因 node 的初始值返回 false)
public boolean contains(T target) {
BTNode<T> node = null;
boolean result = true;
if(root != null)
node = root.find(target);
if(node == null)
result = false;
return result;
}- isEmpty 方法的實現比較簡單,但是我第一次做的時候,將判斷條件寫成了 root.count() == 0,
【注意】樹結構不是連結串列,也不是陣列,count方法是返回 子樹的結點數,所以開始就預設根結點存在了即count方法的返回值至少為1,所以當然不能用在isEmpty方法中。
這裡直接判斷根結點是否為空即可:
//判斷樹是否為空
@Override
public boolean isEmpty() {
return (root == null);
}- toString 方法的思路與之前實現的資料結構(棧、佇列)有些類似,注意這裡要用到遍歷方法,要用到遞迴,所以我用陣列迭代類建立物件,之後層序遍歷輸出。我在實現這個方法時出現了很多報錯,藉助IDEA的提示,才成功解決了問題:
//列印樹
@Override
public String toString(){
UnorderedListADT<BinaryTreeNode<T>> nodes = new ArrayUnorderedList<BinaryTreeNode<T>>();
UnorderedListADT<Integer> levelList = new ArrayUnorderedList<Integer>();
BinaryTreeNode<T> current;
String result = "";
int printDepth = this.getHeight();
int possibleNodes = (int) Math.pow(2, printDepth + 1);
int countNodes = 0;
nodes.addToRear(root);
Integer currentLevel = 0;
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
while (countNodes < possibleNodes) {
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
if (currentLevel > previousLevel) {
result = result + "\n\n";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
} else {
for (int i = 0; i < ((Math.pow(2,
(printDepth - currentLevel + 1)) - 1)); i++) {
result = result + " ";
}
}
if (current != null) {
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
} else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
return result;
}- preorder 和 postorder 方法只需參考給出的 inorder 方法改一下遍歷方式就行:(這三者的遍歷方式都是按子樹進行的,所以框架相同)
@Override
//為樹的前序遍歷返回一個迭代器
public Iterator<T> iteratorPreOrder() {
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
preOrder(root, tempList);
return new TreeIterator(tempList.iterator());
}
private void preOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
if (node != null) {
tempList.addToRear(node.getElement());
inOrder(node.getLeft(), tempList);
inOrder(node.getRight(), tempList);
}
}
@Override
//為樹的後序遍歷返回一個迭代器
public Iterator<T> iteratorPostOrder() {
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
postOrder(root, tempList);
return new TreeIterator(tempList.iterator());
}
private void postOrder(BinaryTreeNode<T> node, ArrayUnorderedList<T> tempList) {
if (node != null) {
inOrder(node.getLeft(), tempList);
inOrder(node.getRight(), tempList);
tempList.addToRear(node.getElement());
}
}
樹-2-中序先序序列構造二叉樹
- 步驟:
(1)確定樹的根結點;(先序遍歷的第一個結點就是二叉樹的根)
(2)求解樹的子樹;(找到根在中序遍歷的位置,位置左邊就是二叉樹的左孩子,位置右邊是二叉樹的右孩子,如果根結點左邊或右邊為空,那麼該方向子樹為空;如果根節點左邊和右邊都為空,那麼根節點已經為葉結點)
(3)對二叉樹的左、右孩子分別進行步驟(1)(2),直到求出二叉樹的結構為止。

樹-3-決策樹
- 這個實驗算是最令人愉悅的一個吧!可以自己設計問題和答案,課本上也有一個示例程式碼可以參考,這樣思路上就比較容易了。
決策樹需要注意的就是不要搞混左子樹和右子樹的物件,在傳遞元素時可以參考書中的格式,先定義元素,再定義對應型別的樹,之後再將元素依次例項化並填入構建的子樹,根據回答迭代輸出問題,直到只剩下最後一層葉結點,輸出判定結果即可:

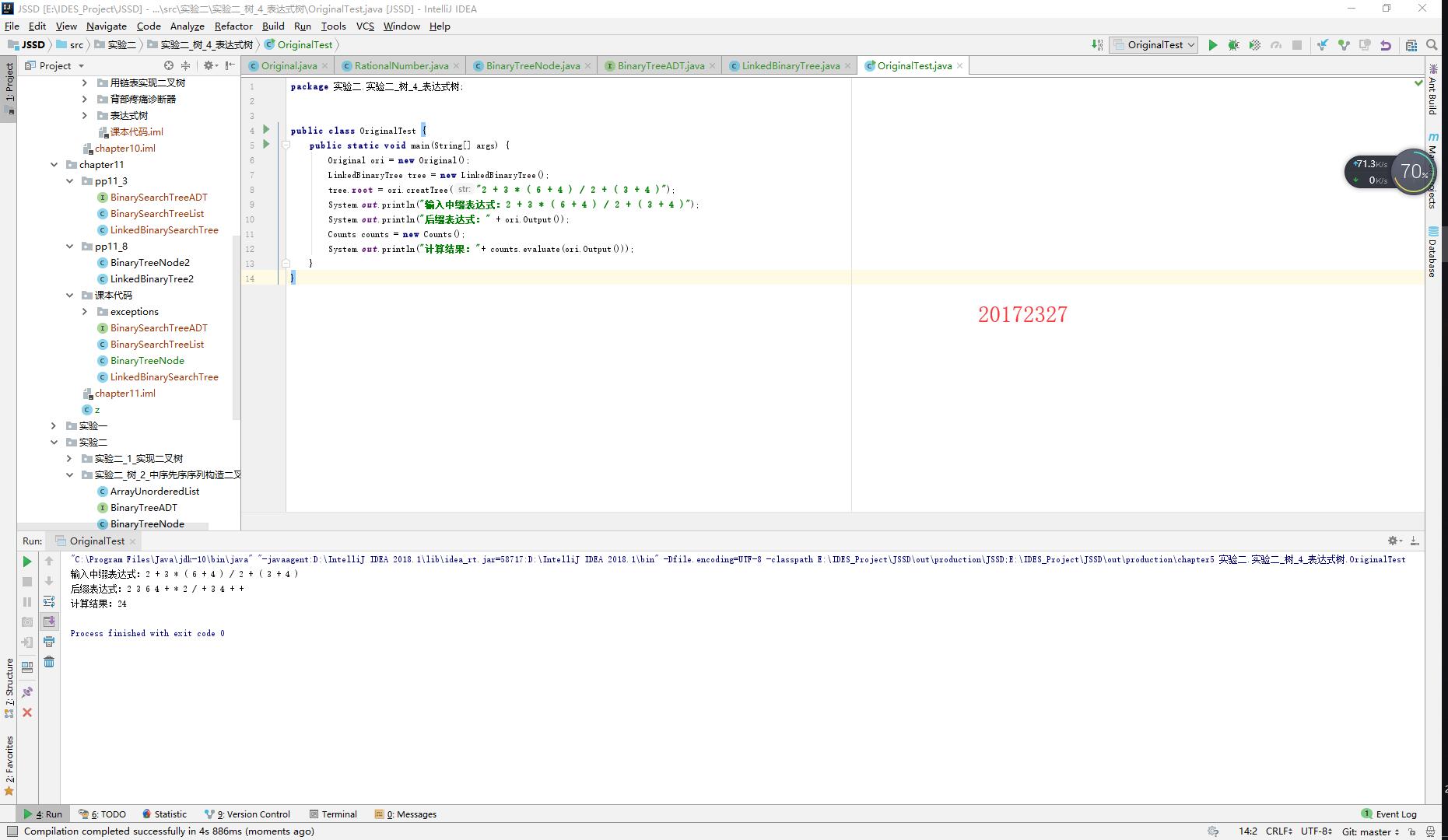
樹-4-表示式樹
- 使用樹來表示算術表示式,我知道一部分,又參考了利用Java實現表示式二叉樹,但還是沒能實現輸入字尾,輸出中綴的情況。這裡的表示式結果輸出我理解為中序輸出,至於輸入我想使用字尾表示式,我繼續查詢相關資料,並參考了其中的部分程式碼:
public class Original extends LinkedBinaryTree{
public BinaryTreeNode creatTree(String str){
StringTokenizer tokenizer = new StringTokenizer(str);
String token;
ArrayList<String> operList = new ArrayList<>();
ArrayList<LinkedBinaryTree> numList = new ArrayList<>();
while (tokenizer.hasMoreTokens()){
token = tokenizer.nextToken();
if(token.equals("(")){
String str1 = "";
while (true){
token = tokenizer.nextToken();
if (!token.equals(")"))
str1 += token + " ";
else break;
}
LinkedBinaryTree S = new LinkedBinaryTree();
S.root = creatTree(str1);
numList.add(S);
}
if(as(token)){
operList.add(token);
}else if(md(token)){
LinkedBinaryTree left = numList.remove(numList.size()-1);
String A = token;
token = tokenizer.nextToken();
if(!token.equals("(")) {
LinkedBinaryTree right = new LinkedBinaryTree(token);
LinkedBinaryTree node = new LinkedBinaryTree(A, left, right);
numList.add(node);
}else {
String str1 = "";
while (true){
token = tokenizer.nextToken();
if (!token.equals(")"))
str1 += token + " ";
else break;
}
LinkedBinaryTree S = new LinkedBinaryTree();
S.root = creatTree(str1);
LinkedBinaryTree node = new LinkedBinaryTree(A,left,S);
numList.add(node);
}
}else
numList.add(new LinkedBinaryTree(token));
}
while(operList.size()>0){
LinkedBinaryTree left = numList.remove(0);
LinkedBinaryTree right = numList.remove(0);
String oper = operList.remove(0);
LinkedBinaryTree node = new LinkedBinaryTree(oper,left,right);
numList.add(0,node);
}
root = (numList.get(0)).root;
return root;
}
private boolean as(String token){
return (token.equals("+")||
token.equals("-"));
}
private boolean md(String token){
return (token.equals("*")||
token.equals("/"));
}
public String Output(){
String result = "";
ArrayList<String> list = new ArrayList<>();
root.postorder(list);
for(String i : list){
result += i+" ";
}
return result;
}
}
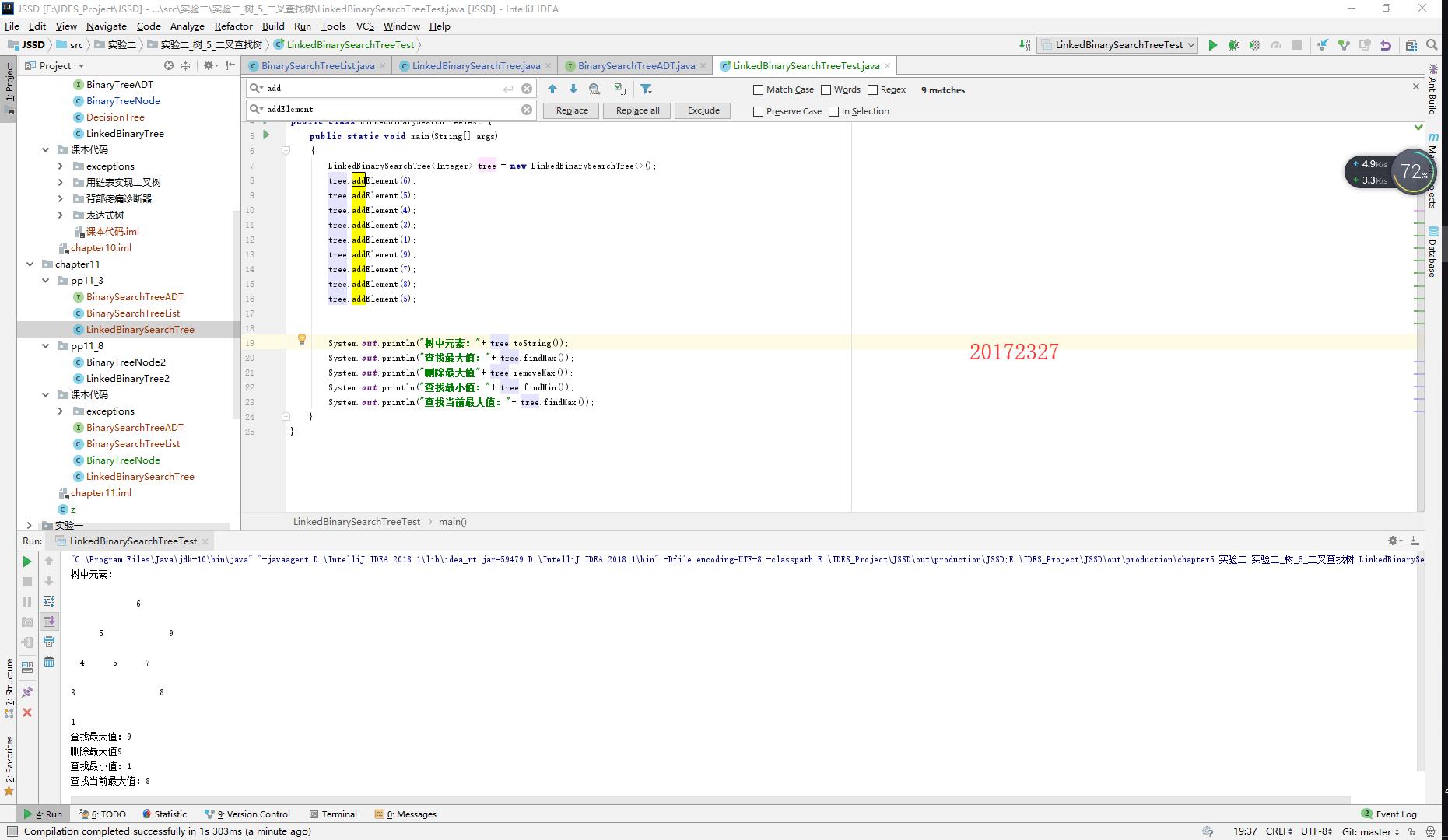
樹-5-二叉查詢樹
- 這個實驗相對容易些,要求實現二叉查詢樹中的方法 findMin 和 findMax,這兩種方法無非是找出二叉查詢樹中的特殊元素,所以可以從遍歷方式上考慮。由於二叉查詢樹的最小元素始終位於整棵樹左下角最後一個左子樹的第一個位置,所以就可以直接返回這個元素的位置,至於怎麼獲取這個元素就可以使用之前的遍歷方法,二叉查詢樹的最小元素是中序遍歷的第一個元素,而後序遍歷就不一定,其他的遍歷方式也不行。於是就返回中序遍歷後的第一個元素即可。
二叉查詢樹中最大元素的查詢過程同理,還是採用中序遍歷最保險,需要使用兩次強轉:
//返回二進位制搜尋中最小值的元素樹.它不會從二進位制搜尋樹中刪除該節點。如果此樹為空, 則丟擲 EmptyCollectionException。
// @return 最小值的元素
// @throws EmptyCollectionException 如果樹是空的
public T findMin() throws EmptyCollectionException
{
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.left == null) {
result = root.element;
//root = root.right;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.left;
while (current.left != null) {
parent = current;
current = current.left;
}
result = current.element;
//parent.left = current.right;
}
//modCount--;
}
return result;
}
//返回在二進位制檔案中具有最高值的元素搜尋樹。 它不會從二進位制檔案中刪除節點搜尋樹。 如果此樹為空, 則丟擲 EmptyCollectionException。
// @return 具有最高值的元素
// @throws EmptyCollectionException 如果樹是空的
public T findMax() throws EmptyCollectionException
{
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.right == null) {
result = root.element;
//root = root.left;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null) {
parent = current;
current = current.right;
}
result = current.element;
//parent.right = current.left;
}
//modCount--;
}
return result;
}
樹-6-紅黑樹分析
- 這兩個類的原始碼比較長,我只針對其中的幾個方法進行了分析。
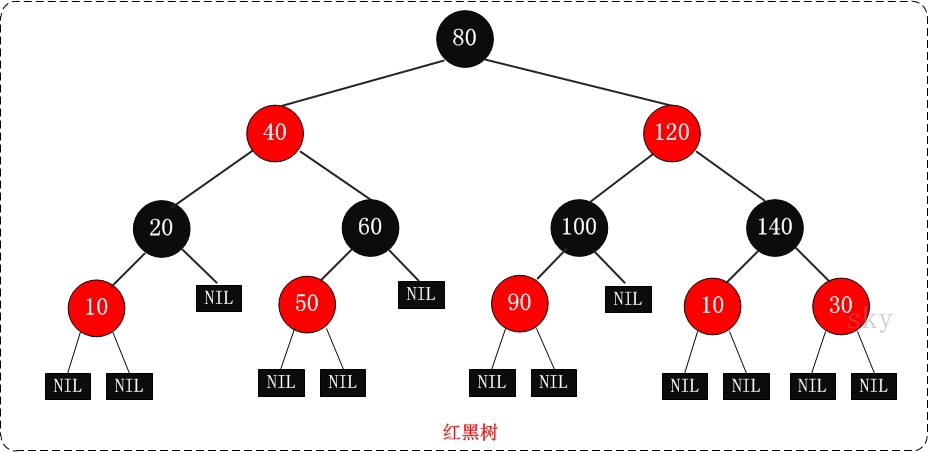
- 首先說說紅黑樹:參考 http://www.cnblogs.com/skywang12345/p/3245399.html
紅黑樹,即 R-B Tree,全稱是Red-Black Tree,它一種特殊的二叉查詢樹。紅黑樹的每個結點上都有儲存位表示結點的顏色,可以是紅(Red)或黑(Black)。 - 紅黑樹的特性:
(1)每個結點或者是黑色,或者是紅色。
(2)根結點是黑色。
(3)每個葉結點(NIL)是黑色。 【注意:這裡葉結點,是指為空(NIL或NULL)的葉結點!】
(4)如果一個結點是紅色的,則它的子節點必須是黑色的。
(5)從一個結點到該結點的子孫結點的所有路徑上包含相同數目的黑結點。
【注意:特性(3)中的葉結點,是隻為空(NIL或null)的結點。
特性(5),確保沒有一條路徑會比其他路徑長出倆倍。因而,紅黑樹是相對是接近平衡的二叉樹。】 紅黑樹示意圖:
- TreeMap類:
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable
----------------------------------------------------------------
//TreeMap 是一個有序的key-value集合,它是通過紅黑樹實現的。
//TreeMap 繼承於AbstractMap,所以它是一個Map,即一個key-value集合。
//TreeMap 實現了NavigableMap介面,意味著它支援一系列的導航方法。比如返回有序的key集合。
//TreeMap 實現了Cloneable介面,意味著它能被克隆。
//TreeMap 實現了java.io.Serializable介面,意味著它支援序列化。- firstEntry()和getFirstEntry()方法:
public Map.Entry<K,V> firstEntry() {
return exportEntry(getFirstEntry());
}
final Entry<K,V> getFirstEntry() {
Entry<K,V> p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}firstEntry() 和 getFirstEntry() 都是用於獲取第一個節點。firstEntry() 是對外介面;getFirstEntry() 是內部介面。而且,firstEntry() 是通過 getFirstEntry() 來實現的。
- HashMap類:
初始容量與載入因子是影響HashMap的兩個重要因素:
public HashMap(int initialCapacity, float loadFactor)初始容量預設值:
/**
* The default initial capacity - MUST be a power of two.
*/
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16載入因子預設值:
/**
* The load factor used when none specified in constructor.
*/
static final float DEFAULT_LOAD_FACTOR = 0.75f;- containsValue類:
public boolean containsValue(Object value) {
Node<K,V>[] tab; V v;
if ((tab = table) != null && size > 0) {
for (int i = 0; i < tab.length; ++i) {
for (Node<K,V> e = tab[i]; e != null; e = e.next) {
if ((v = e.value) == value ||
(value != null && value.equals(v)))
return true;
}
}
}
return false;
}如果在map中包含對應的特定的鍵值則返回true,否則返回false。
三、實驗過程中遇到的問題和解決過程
問題出現了好多,但我都解決了,忘截圖了,所以這地我也不知道寫點啥。
四、感悟
通過這次實驗,我發現我對這段時間樹的學習並部紮實,有些基本的還是記不住,在邏輯推理的過程中,遇到的麻煩也比較多。這次實驗讓我知道了,最近的不足,也讓我決定抽出更多時間去學習Java。
