深度學習 --- 神經網路的學習原理(學習規則)
從今天開始進入深度學習領域,深度學習我在前兩年的理論學習過程中,體會頗深,其中主要有兩個演算法CNN和RNN,但是本人喜歡追本溯源,喜歡刨根問題。最重要的是每個演算法並不是拍腦袋想出來的,是根據當時的研究程序和研究環境有關,因此想要深入理解深度學習的精髓,我們需要去了解,深度學習因為什麼被提出來的,解決了什麼問題,為什麼能解決問題以及這個演算法和機器學習有什麼本質的區別等等。想要回答這些問題,就不能上來就學習CNN和RNN,我們需要尋找問題的根源,通過引入問題,然後為了解決這個問題在引入深度學習,這時候才符合我們的認知規律,而不是本末倒置,本末倒置的後果是對演算法理解的不深,更不會使用這個演算法,當然時間長了自然理解,但是這總歸沒有體系化,你說呢?學習知識不在於你學了多少,而是在於你內化多少,遇到問題時能輸出多少,這才是最有效率的學習。在這裡我計劃從最簡單的問題開始,一步步深入下去,直到CNN和RNN,然後針對這兩個演算法再好好的實戰,當然,一旦這兩個演算法學好以後就可以多學習這兩個演算法的衍生演算法,因此理解很重要,內化更重要,到公司以後知識的輸出更重要。好,廢話不多說,今天就開始,本節主要介紹神經網路的總體的模型,介紹不同的學習規則,這些規則在以後的文章中都會使用到,所以請大家多留心。
在機器學習中,我們知道有監督學習,無監督學習和半監督學習,在神經網路中分為監督學習、無監督學習和灌輸式學習。
監督學習也叫有導師學習,這種學習模式採用糾錯規則,即需要給網路不斷輸入資料,把神經網路輸出和期望輸出的相比較,當兩者不同時,根據差錯方向和大小按一定規則調整權值,以使下一步網路更接近期望結果,一旦當網路對於各種給定的輸入均能引數所期望的輸出時,即認為網路學會了,就可以用來工作了。
無監督學習也叫無導師學習,學習過程中需要不斷的給網路提供動態的輸入資訊,網路能根據特有的內部結構和學習規則,再輸入的資訊中去發現任何可能存在的模式和規律,同時能根據網路的功能和輸入資訊調整權值,這個過程稱為網路的自組織,其結果就是使網路能對屬於同一類的模式進行自動的分類,在這種學習模式中,網路的權值調整不取決於外來的教師訊號,而是取決於網路的內部。
灌輸式學習是指將網路設計成能記憶特別的例子,以後當給定有關該例子的輸入資訊時,例子便會被回憶起來。網路權值一旦設計好就不在變動,因此學習是一次性的而不是一個訓練過程。
下面給出神經網路權值調整的通用規則,該規則是由日本著名神經網路學者Amari與1990年提出的:

上圖中神經元j是神經網路中的某個節點,其輸入用向量表示,該輸入可以是來自網路的外部,也可以來自其他神經元的輸出。第i個輸入與神經元j的連線權值用
表示,連線到神經元j的全部權值構成了權向量
,其中
對應神經元的閾值,對應的輸入分量x0恆為-1,圖中
代表學習訊號(r是regulation的縮寫即學習規則),該訊號通常是
通用學習規則的表示式為:
權向量的在t時刻的調整量
與t時刻的輸入向量
和學習訊號r乘積成正比,用數學表示式為:
式子中的為正數,稱為學習常數,其值決定了學習的速率,下一時刻的權向量應為:
不同的學習規則對有不同的意義,也是形成不同的神經網路的原因,因此下面將重點介紹這些學習規則,這些規則是網路的學習本質,請大家好好體會,我也會盡可能的講解深入,同時這些規則在後面的網路中都會使用,例如BP等。
1.Hebb學習規則
1949年,心理學家D.O.Hebb最早提出了關於神經網路學習機理的‘突觸修正’的假設。當神經元i與神經元j同時處於興奮狀態時,兩者之間的連線強度應增強。
在Hebb學習規則中,學習訊號簡單的等於神經元的輸出:
權向量的調整公式為:
權向量中,每個分量的調整由下式確定:
從上式可以看出。權值調整向量與輸入輸出乘積成正比,因此經常出現的輸入模式對權向量影響很大,因此需要預先設定權飽和值,防止權值無限增長。
2.Perceptron學習規則
1958年,美國學者Frank Rosenblatt 首次提出感知器,感知器的學習規則也由此誕生,該規則規定,學習訊號等於神經元期望輸出與實際輸出的之差:
式中,為期望輸出,
,感知器採用符號函式作為轉移函式,其表示式為;
因此權值調整公式為:
從上式我們可以看到,當實際輸出和期望值值相同時,權值不調整,反之調整,權值調整公式可化簡為:
感知器學習規則只適用於二進位制神經元,初值可任取。
3.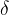 學習規則
學習規則
1986年,認知心理學家McClelland 和 Rumelhart在神經網路訓練中引入了規則,該規則稱為連續感知器學習規則,與上面的離散感知器類似,
規則的學習訊號規定為:
上式的學習訊號稱為,式中
是轉移函式
的導數,顯然
規則要求啟用函式可導。如Sigmoid函式
事實,規則可以通過輸出值和期望值的最小平方誤差推倒。定義神經元輸出值與期望值的最小平方誤差為:
其中,誤差E是權向量的函式,為了使E最小,
應與誤差的負梯度成正比即:
其中,梯度為:
權值調整公式為:
由此可看到上式的中間項和r是相同的,因此它是根據梯度進行迭代更新的,BP就是使用這個學習規則。
4.LMS學習規則
1962年BernardWrow和Marcian Hoff提出了Widrow-Hoff學習規則,因為它能使神經元實際輸出與期望輸出之間的平方差最小,所以又稱為最小均方規則(LMS),學習規則如下定義:
權向量的調整量為:
的各分量為:
實際上,LMS是學習規則的一種特殊情況,如果是
,則
,此時
學習規則的學習規則就是LMS的學習規則,該學習規則好處是不需要對啟用函式求導,學習速度快,精度較高。
5.Corrclation學習規則
Correlation(相關)學習規則規定學習訊號為:
得到和
分別為:
該規則表明,當dj是xi的期望輸出時,相應的權值增量就是期望和輸入的乘積。
如果Hebb學習規則中的轉移函式為二進位制函式,且有,則相關學習規則可看著Hebb的一種特殊情況。
6. Winner - Take - All學習規則
Winner - Take - All(勝者為王)學習規則是一種競爭關係的學習規則,用於無監督學習,一般將網路的某一層確定為競爭層,對於一個特定的輸入x,競爭層的所有的p個神經元均有輸出響應,其中響應值最大的神經元為在競爭中獲勝的神經元,即:
只有獲勝的神經元才有權調整其向量Wm,調整量為:
由於兩個向量的點積越大,表明兩者越相近,所以調整獲勝神經元權值的結果是使wm進一步接近當前輸入x,顯然下次出現與x相似的輸入模式時,上次獲勝的神經元更容易獲勝,在反覆的競爭學習中,競爭層的個各神經元所對應的權向量被逐漸調整為輸入樣本空間的聚類中心。
還有一個是外星節點學習規則,上面這個為內星學習規則,外星和其類似。
下面給出對比列表:

各個學習之間並不是完全獨立的,這幾個學習規則在下面的神經網路中都會用到,到時再細講,下一節就開始講BP,大家就知道了。剛開始看這些東西可能感覺不理解,大家只需知道有這個學習規則就行,等學習具體的神經網路時就一且明朗了,好本節到此結束,下一節開始BP神經網路。
