凸優化和非凸優化
阿新 • • 發佈:2018-11-11
數學中最優化問題的一般表述是求取,使
,其中
是n維向量,
是
的可行域,
是
上的實值函式。
是閉合的凸集且
是
上的凸函式的最優化問題,這兩個條件任一不滿足則該問題即為非凸的最優化問題。
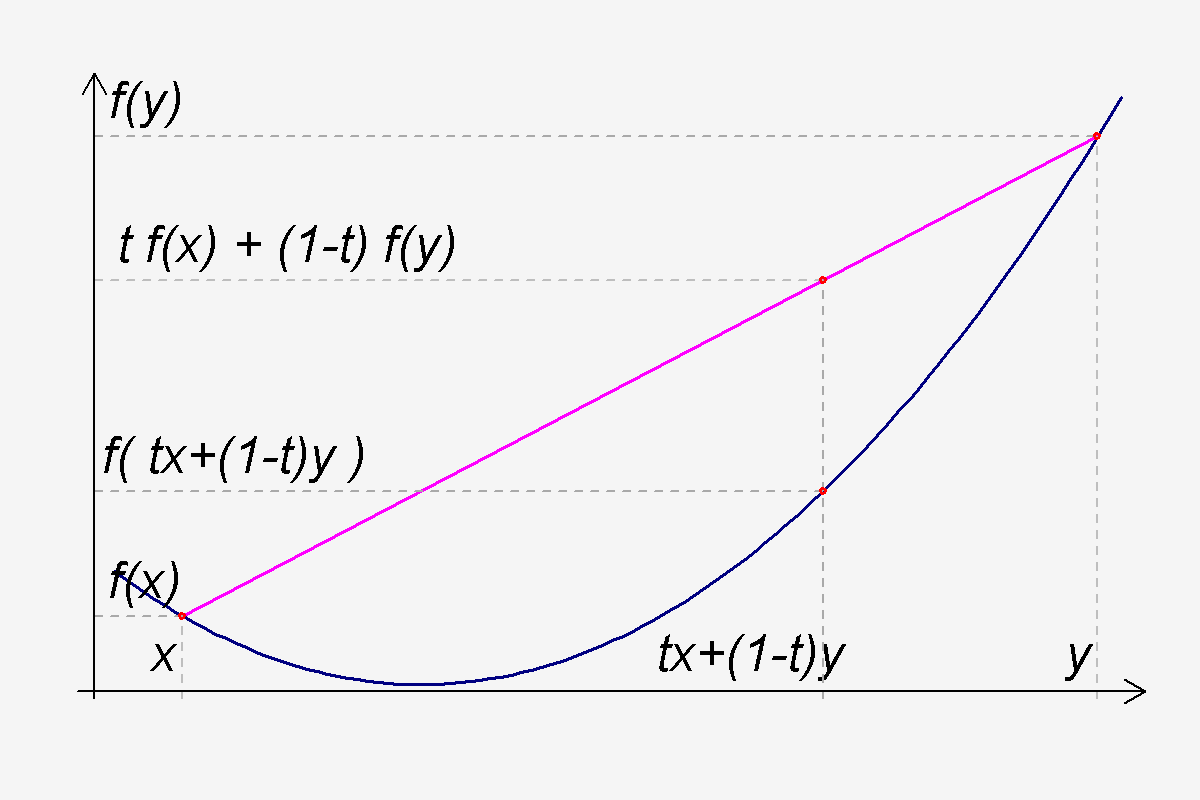
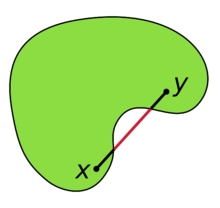
其中,是 凸集是指對集合中的任意兩點
,有
,即任意兩點的連線段都在集合內,直觀上就是集合不會像下圖那樣有“凹下去”的部分。
至於閉合的凸集,則涉及到閉集的定義,而閉集的定義又基於開集,比較抽象,不贅
述,這裡可以簡單地認為閉合的凸集是指包含有所有邊界點的凸集。
注意:中國大陸數學界某些機構關於函式凹凸性定義和國外的定義是相反的。Convex Function在某些中國大陸的數學書中指凹函式。Concave Function指凸函式。但在中國大陸涉及經濟學的很多書中,凹凸性的提法和其他國家的提法是一致的,也就是和數學教材是反的。舉個例子,同濟大學高等數學教材對函式的凹凸性定義與本條目相反,本條目的凹凸性是指其上方圖是凹集或凸集,而同濟大學高等數學教材則是指其下方圖是凹集或凸集,兩者定義正好相反。
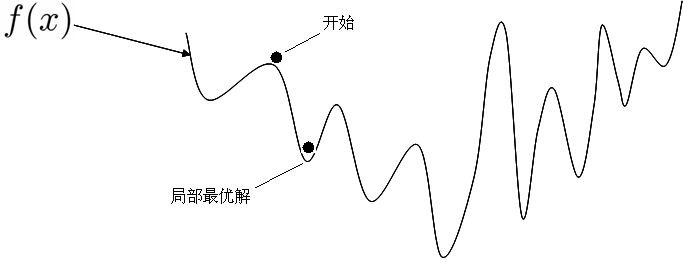
為什麼要求是凸函式呢?因為如果是下圖這樣的函式,則無法獲得全域性最優解。
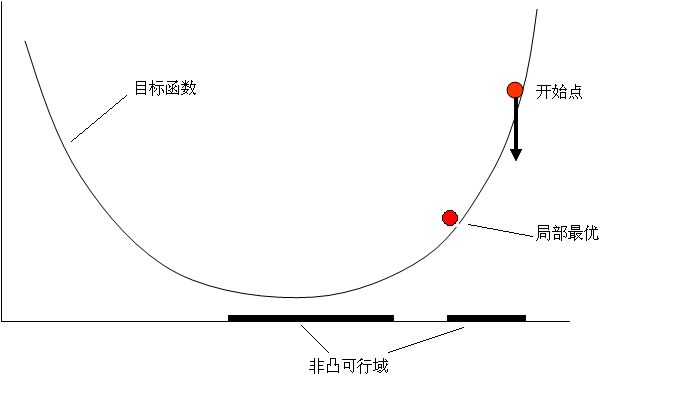
為什麼要求是凸集呢?因為如果可行域不是凸集,也會導致區域性最優
實際建模中判斷一個最優化問題是不是凸優化問題一般看以下幾點:
- 目標函式
如果不是凸函式,則不是凸優化問題
- 決策變數
中包含離散變數(0-1變數或整數變數),則不是凸優化問題
- 約束條件寫成
時,
如果不是凸函式,則不是凸優化問題
之所以要區分凸優化問題和非凸的問題原因在於凸優化問題中區域性最優解同時也是全域性最優解,這個特性使凸優化問題在一定意義上更易於解決,而一般的非凸最優化問題相比之下更難解決。
非凸優化問題如何轉化為凸優化問題的方法:
1)修改目標函式,使之轉化為凸函式
2)拋棄一些約束條件,使新的可行域為凸集並且包含原可行域