題意翻譯

DZY熱愛化學.他有n種物質,其中m對會反應.他把它們一種一種倒到燒杯裡.有一個危險值,一開始等於1.如果一種物質倒到燒杯裡之後至少有一種物質能和它反應,則危險值乘以二;否則危險值不變.求所有物質倒到燒杯裡之後最大的危險值.

By @Fuko_Ibuki

題目描述

DZY loves chemistry, and he enjoys mixing chemicals.

DZY has n n n chemicals, and m m m pairs of them will react. He wants to pour these chemicals into a test tube, and he needs to pour them in one by one, in any order.

Let's consider the danger of a test tube. Danger of an empty test tube is 1 1 1 . And every time when DZY pours a chemical, if there are already one or more chemicals in the test tube that can react with it, the danger of the test tube will be multiplied by 2 2 2 . Otherwise the danger remains as it is.

Find the maximum possible danger after pouring all the chemicals one by one in optimal order.

輸入輸出格式

輸入格式：

The first line contains two space-separated integers n n n and m m m .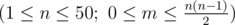

Each of the next m m m lines contains two space-separated integers xi x_{i} xi​ and yi y_{i} yi​ (1<=xi<yi<=n) (1<=x_{i}<y_{i}<=n) (1<=xi​<yi​<=n) . These integers mean that the chemical xi x_{i} xi​ will react with the chemical yi y_{i} yi​ . Each pair of chemicals will appear at most once in the input.

Consider all the chemicals numbered from 1 1 1 to n n n in some order.

輸出格式：

Print a single integer — the maximum possible danger.

輸入輸出樣例

輸入樣例#1： 複製

1 0

輸出樣例#1： 複製

1

輸入樣例#2： 複製

2 1
1 2

輸出樣例#2： 複製

2

輸入樣例#3： 複製

3 2
1 2
2 3

輸出樣例#3： 複製

4

說明

In the first sample, there's only one way to pour, and the danger won't increase.

In the second sample, no matter we pour the 1 1 1 st chemical first, or pour the 2 2 2 nd chemical first, the answer is always 2 2 2 .

In the third sample, there are four ways to achieve the maximum possible danger: 2-1-3, 2-3-1, 1-2-3 and 3-2-1 (that is the numbers of the chemicals in order of pouring).

用並查集維護即可；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 100005
#define inf 0x3f3f3f3f
#define INF 999999999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 20100403
#define sq(x) (x)*(x)
#define eps 1e-5
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

int n, m;
ll ans;
int fa[maxn];

void init() {
	for (int i = 0; i <= n; i++)fa[i] = i;
}

int findfa(int x) {
	if(x == fa[x])return x;
	return fa[x] = findfa(fa[x]);
}

void merge(int x, int y) {
	if (findfa(x) != findfa(y)) {
		fa[findfa(x)] = findfa(y);
	}
}

int main()
{
	//ios::sync_with_stdio(false);
	rdint(n); rdint(m);
	init(); ll ans = 1;
	while (m--) {
		int x, y;
		rdint(x); rdint(y);
		merge(x, y);
	}
	int tot = 0;
	for (int i = 1; i <= n; i++) {
		if (fa[i] == i)tot++;
	}
	cout << ((ll)1 << (n - tot)) << endl;
    return 0;
}