DFS(深搜)演算法
阿新 • • 發佈:2018-11-12
深度優先搜尋(DFS) 深度優先搜尋在搜尋過程中訪問某個頂點後,需要遞迴地訪問此頂點的所有未訪問過的相鄰頂點。 初始條件下所有節點為白色,選擇一個作為起始頂點,按照如下步驟遍歷: a. 選擇起始頂點塗成灰色,表示還未訪問 b. 從該頂點的鄰接頂點中選擇一個,繼續這個過程(即再尋找鄰接結點的鄰接結點),一直深入下去,直到一個頂點沒有鄰接結點了,塗黑它,表示訪問過了 c. 回溯到這個塗黑頂點的上一層頂點,再找這個上一層頂點的其餘鄰接結點,繼續如上操作,如果所有鄰接結點往下都訪問過了,就把自己塗黑,再回溯到更上一層。 d. 上一層繼續做如上操作,知道所有頂點都訪問過。 用圖可以更清楚的表達這個過程:
1.初始狀態,從頂點1開始
2.依次訪問過頂點1,2,3後,終止於頂點3
3.從頂點3回溯到頂點2,繼續訪問頂點5,並且終止於頂點5
4.從頂點5回溯到頂點2,並且終止於頂點2
5.從頂點2回溯到頂點1,並終止於頂點1
6.從頂點4開始訪問,並終止於頂點4
從頂點1開始做深度搜索:
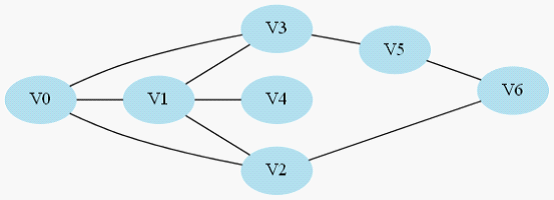
![]() 假設按照以下的順序來搜尋:
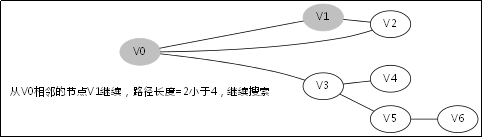
1.V0->V1->V4,此時到底盡頭,仍然到不了V6,於是原路返回到V1去搜索其他路徑;
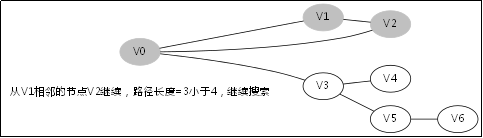
2.返回到V1後既搜尋V2,於是搜尋路徑是V0->V1->V2->V6,,找到目標節點,返回有解。
3.1.舉例
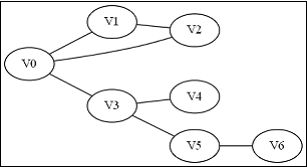
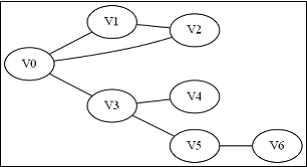
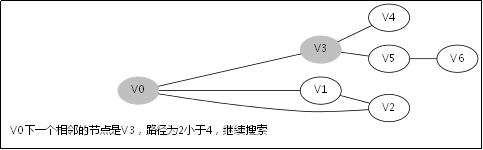
給出如圖3-1所示的圖,求圖中的V0出發,是否存在一條路徑長度為4的搜尋路徑。
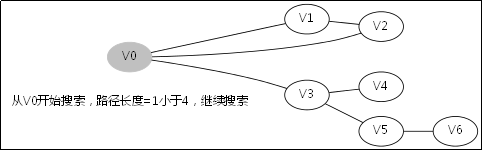
假設按照以下的順序來搜尋:
1.V0->V1->V4,此時到底盡頭,仍然到不了V6,於是原路返回到V1去搜索其他路徑;
2.返回到V1後既搜尋V2,於是搜尋路徑是V0->V1->V2->V6,,找到目標節點,返回有解。
3.1.舉例
給出如圖3-1所示的圖,求圖中的V0出發,是否存在一條路徑長度為4的搜尋路徑。
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3.3.對應例子的虛擬碼
這裡先給出上邊處理過程的對應虛擬碼。
Cpp程式碼
3.3.對應例子的虛擬碼
這裡先給出上邊處理過程的對應虛擬碼。
Cpp程式碼
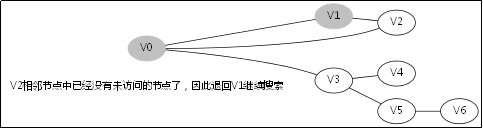
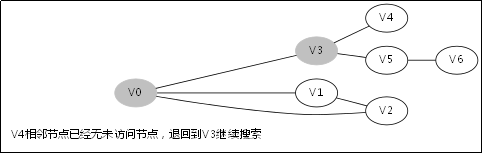
![]() 此後堆疊呼叫返回到V0那一層,因為V1那一層也找不到跟V1的相鄰未訪問節點
此後堆疊呼叫返回到V0那一層,因為V1那一層也找不到跟V1的相鄰未訪問節點
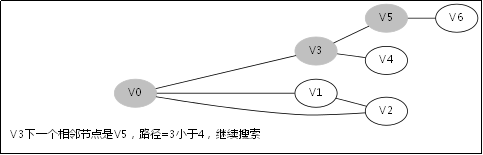
![]() 此後堆疊呼叫返回到V3那一層
此後堆疊呼叫返回到V3那一層
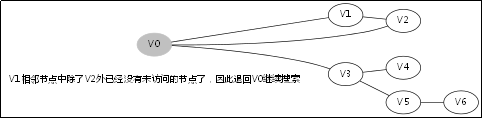
![]() 此後堆疊呼叫返回到主函式呼叫DFS(V0,0)的地方,因為已經找到解,無需再從別的節點去搜別的路徑了。
DFS 演算法
思想:一直往深處走,直到找到解或者走不下去為止
此後堆疊呼叫返回到主函式呼叫DFS(V0,0)的地方,因為已經找到解,無需再從別的節點去搜別的路徑了。
DFS 演算法
思想:一直往深處走,直到找到解或者走不下去為止
 BFS演算法
BFS演算法
 DFS:使用棧儲存未被檢測的結點,結點按照深度優先的次序被訪問並依次被壓入棧中,並以相反的次序出棧進行新的檢測。
DFS:使用棧儲存未被檢測的結點,結點按照深度優先的次序被訪問並依次被壓入棧中,並以相反的次序出棧進行新的檢測。
 BFS:使用佇列儲存未被檢測的結點。結點按照寬度優先的次序被訪問和進出佇列。
BFS:使用佇列儲存未被檢測的結點。結點按照寬度優先的次序被訪問和進出佇列。

- 初始狀態,從頂點1開始
- 依次訪問過頂點1,2,3後,終止於頂點3
- 從頂點3回溯到頂點2,繼續訪問頂點5,並且終止於頂點5
- 從頂點5回溯到頂點2,並且終止於頂點2
- 從頂點2回溯到頂點1,並終止於頂點1
- 從頂點4開始訪問,並終止於頂點4













- /**
- * DFS核心虛擬碼
- * 前置條件是visit陣列全部設定成false
- * @param n 當前開始搜尋的節點
- * @param d 當前到達的深度,也即是路徑長度
- * @return 是否有解
- */
- bool DFS(Node n, int d){
- if (d == 4){//路徑長度為返回true,表示此次搜尋有解
- return true;
- }
- for (Node nextNode in n){//遍歷跟節點n相鄰的節點nextNode,
- if (!visit[nextNode]){//未訪問過的節點才能繼續搜尋
- //例如搜尋到V1了,那麼V1要設定成已訪問
- visit[nextNode] = true;
- //接下來要從V1開始繼續訪問了,路徑長度當然要加
- if (DFS(nextNode, d+1)){//如果搜尋出有解
- //例如到了V6,找到解了,你必須一層一層遞迴的告訴上層已經找到解
- return true;
- }
- //重新設定成未訪問,因為它有可能出現在下一次搜尋的別的路徑中
- visit[nextNode] = false;
- }
- //到這裡,發現本次搜尋還沒找到解,那就要從當前節點的下一個節點開始搜尋。
- }
- return false;//本次搜尋無解
- }
 BFS演算法
BFS演算法
 DFS:使用棧儲存未被檢測的結點,結點按照深度優先的次序被訪問並依次被壓入棧中,並以相反的次序出棧進行新的檢測。
DFS:使用棧儲存未被檢測的結點,結點按照深度優先的次序被訪問並依次被壓入棧中,並以相反的次序出棧進行新的檢測。
 BFS:使用佇列儲存未被檢測的結點。結點按照寬度優先的次序被訪問和進出佇列。
BFS:使用佇列儲存未被檢測的結點。結點按照寬度優先的次序被訪問和進出佇列。

