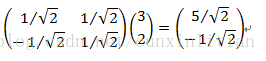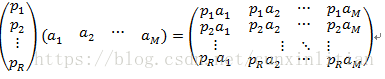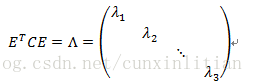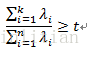13 降維

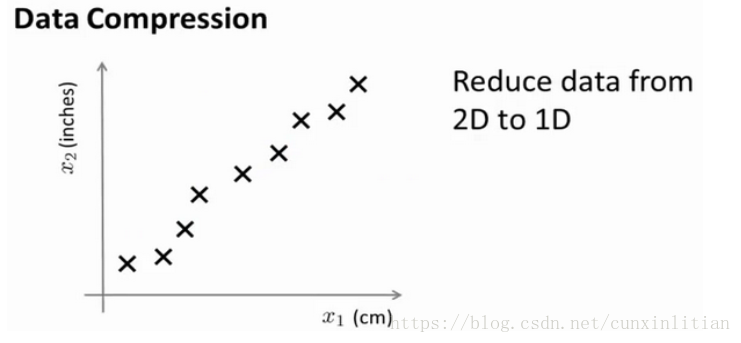
13.1 動機一：資料壓縮

假設兩個未知的特徵：是用釐米表示長度；是用英寸表示同一物體的長度。這是一種高度冗餘的表示。希望將這個二維的資料降至一維，即資料壓縮。

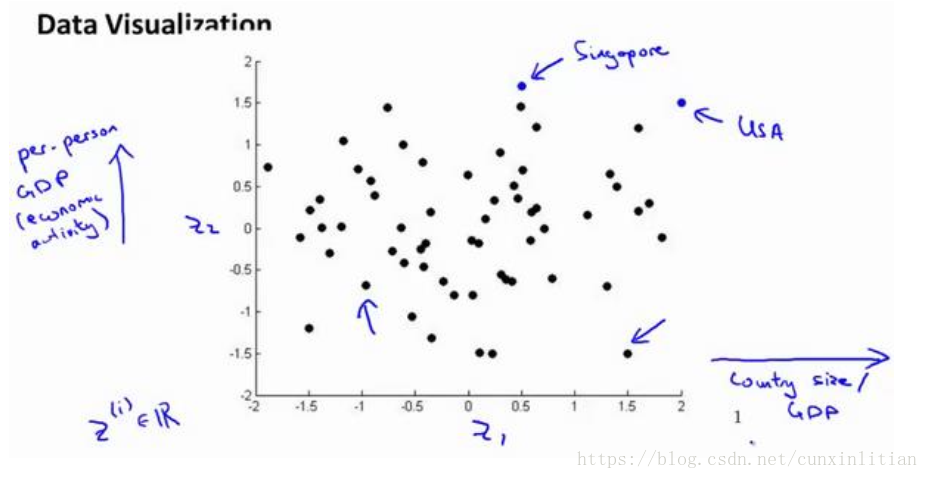
13.2 動機二：資料視覺化化

降維可以使資料視覺化。關於許多不同國家的資料，每一個特徵向量都有50個特徵（如 GDP，人均 GDP，平均壽命等）。如果要將這個50維的資料視覺化是不可能的。使用降維的方法將其降至2維，便可以將其可視化了。

這樣做的問題在於，降維的演算法只負責減少維數，新產生的特徵的意義就必須由自己去發現了。

13.3 主成分分析問題

主成分分析（Principal components analysis，以下簡稱PCA）是最重要的降維方法之一。在資料壓縮消除冗餘和資料噪音消除等領域都有廣泛的應用。它是一個線性變換。這個變換把資料變換到一個新的座標系統中，使得任何資料投影的第一大方差在第一個座標(稱為第一主成分)上，第二大方差在第二個座標(第二主成分)上，依次類推。主成分分析經常用減少資料集的維數，同時保持資料集的對方差貢獻最大的特徵。

PCA 技術的一個很大的優點是，它是完全無引數限制的。在 PCA 的計算過程中完全不需要人為的設定引數或是根據任何經驗模型對計算進行干預，最後的結果只與資料相關，與使用者是獨立的。

但是，這一點同時也可以看作是缺點。如果使用者對觀測物件有一定的先驗知識，掌握了資料的一些特徵，卻無法通過引數化等方法對處理過程進行干預，可能會得不到預期的效果，效率也不高。

13.4 PCA的數學原理

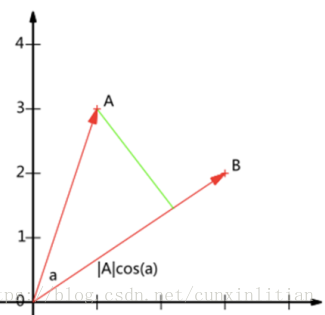
1）內積與投影

如圖，A與B的內積等於A到B的投影長度乘以B的模：A⋅B=|A||B|cos(a)。如果我們假設B的模為1，即讓|B|=1，那麼就變成了：A⋅B=|A|cos(a)。則可得到結論：設向量B的模為1，則A與B的內積值等於A向B所在直線投影的向量長度。

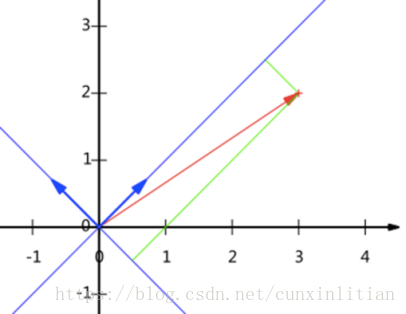
2）基與基變換

如圖，向量可以表示為（3，2）。要準確描述向量，首先要確定一組基，然後給出在基所在的各個直線上的投影值。只不過我們經常省略第一步，而預設以（1，0）和（0，1）為基。

實際上，對應任何一個向量我們總可以找到其同方向上模為1的向量，只要讓兩個分量分別除以模就好了。例如，上面的基可以變為：（1/ ，1/ ）和（-1/ ，1/ ），不難得到新的座標為：（5/ ，-1/ ）。

將(3,2)變換為新基上的座標，就是用(3,2)與第一個基做內積運算，作為第一個新的座標分量，然後用(3,2)與第二個基做內積運算，作為第二個新座標的分量。即：

稍微推廣一下，如果我們有m個二維向量，只要將二維向量按列排成一個兩行m列矩陣，然後用“基矩陣”乘以這個矩陣，就得到了所有這些向量在新基下的值。例如(1,1)，(2,2)，(3,3)，想變換到剛才那組基上，即

一般的，如果我們有M個N維向量，想將其變換為由R個N維向量表示的新空間中，那麼首先將R個基按行組成矩陣A，然後將向量按列組成矩陣B，那麼兩矩陣的乘積AB就是變換結果，其中AB的第m列為A中第m列變換後的結果。如下圖，pi是一個行向量，表示第i個基，aj是一個列向量，表示第j個原始資料記錄。

所以，二維降為一維時：尋找一個一維基，使得所有資料變換為這個基上的座標表示後，方差值最大。三維降為二維時：到一個方向使得投影后方差最大，這樣就完成了第一個方向的選擇，繼而我們選擇第二個投影方向。若還是單純只選擇方差最大的方向，很明顯，這個方向與第一個方向應該是“幾乎重合在一起”，顯然這樣的維度是沒有用的。讓兩個欄位儘可能表示更多的原始資訊，我們是不希望它們之間存在（線性）相關性的。可以用兩個欄位的協方差表示其相關性。協方差為0，它們之間不存在相關性。

3）協方差矩陣及優化目標

協方差為0時，表示兩個欄位完全獨立。優化目標為：將一組N維向量降為K維（K大於0，小於N），其目標是選擇K個單位（模為1）正交基，使得原始資料變換到這組基上後，各欄位兩兩間協方差為0，而欄位的方差則儘可能大（在正交的約束下，取最大的K個方差）。

假設只有a和b兩個欄位，那麼我們將它們按行組成矩陣X，即：

用X乘以X的轉置，並乘上係數1/m，即：

設我們有m個n維資料記錄，將其按列排成n乘m的矩陣X，設

則C是一個對稱矩陣，其對角線分別個各個欄位的方差，而第i行j列和j行i列元素相同，表示i和j兩個欄位的協方差。

4）協方差矩陣對角化

要達到優化目標，等價於將協方差矩陣對角化：即除對角線外的其它元素化為0，並且在對角線上將元素按大小從上到下排列，這樣我們就達到了優化目的。

設原始資料矩陣X對應的協方差矩陣為C，而P是一組基按行組成的矩陣，設Y=PX，則Y為X對P做基變換後的資料。設Y的協方差矩陣為D，推導一下D與C的關係：

優化目標變成了尋找一個矩陣P，滿足PCPT是一個對角矩陣，並且對角元素按從大到小依次排列，那麼P的前K行就是要尋找的基，用P的前K行組成的矩陣乘以X就使得X從N維降到了K維並滿足上述優化條件。

一個n行n列的實對稱矩陣一定可以找到n個單位正交特徵向量，設這n個特徵向量為，我們將其按列組成矩陣：E=()。參考線性代數書籍關於“實對稱矩陣對角化”的內容對協方差矩陣C有如下結論：

即P=ET，P是協方差矩陣的特徵向量單位化後按行排列出的矩陣，其中每一行都是C的一個特徵向量。如果設P按照Λ中特徵值的從大到小，將特徵向量從上到下排列，則用P的前K行組成的矩陣乘以原始資料矩陣X，就得到了我們需要的降維後的資料矩陣Y。

13.5 PCA演算法步驟

由PCA的數學原理可以將PCA的演算法步驟歸納如下：

    1）將原始資料按列組成n行m列矩陣X。

2）將X的每一行（代表一個屬性欄位）進行零均值化，即減去這一行的均值。

3）求出協方差矩陣。

4）求出協方差矩陣的特徵值及對應的特徵向量。

1. 將特徵向量對應特徵值大小從上到下按行排列成矩陣，取前k行組成矩陣P。

2. Y=PX即為降維到k維後的資料。

13.6 選擇主成分的數量

通常主成分的數量k的選取有兩種方法：

1. 通過交叉驗證法選取較好的k。

2. 從演算法原理的角度設定一個閥值，比如t=99%，然後選取使得下式成立的最小k的值：

       其中從大到小排列。

13.7 錯誤使用PCA的情況

錯誤的主要成分分析情況：一個常見錯誤使用主要成分分析的情況是，將其用於減少過擬合（減少了特徵的數量）。這樣做非常不好，不如嘗試正則化處理。原因在於主要成分分析只是近似地丟棄掉一些特徵，它並不考慮任何與結果變數有關的資訊，因此可能會丟失非常重要的特徵。然而當我們進行正則化處理時，會考慮到結果變數，不會丟掉重要的資料。

另一個常見的錯誤是，預設地將主要成分分析作為學習過程中的一部分，這雖然很多時候有效果，最好還是從所有原始特徵開始，只在有必要的時候（演算法執行太慢或者佔用太多記憶體）才考慮採用主要成分分析。