顏色直方圖+餘弦相似度 c++opencv實現
阿新 • • 發佈:2018-11-12
原理部分來自阮一峰部落格
http://www.ruanyifeng.com/blog/2013/03/similar_image_search_part_ii.html
顏色分佈法:
每張圖片都可以生成顏色分佈的直方圖(color histogram)。如果兩張圖片的直方圖很接近,就可以認為它們很相似。
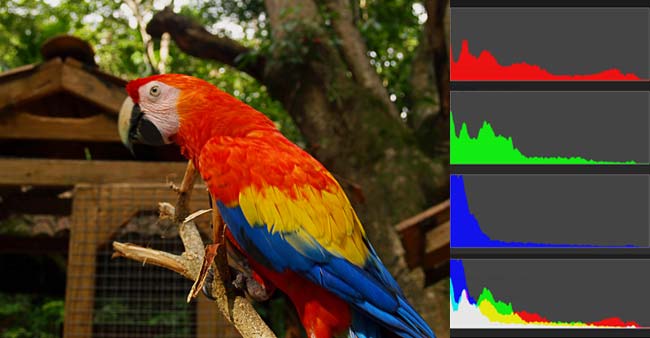
任何一種顏色都是由紅綠藍三原色(RGB)構成的,所以上圖共有4張直方圖(三原色直方圖 + 最後合成的直方圖)。
如果每種原色都可以取256個值,那麼整個顏色空間共有1600萬種顏色(256的三次方)。針對這1600萬種顏色比較直方圖,計算量實在太大了,因此需要採用簡化方法。可以將0~255分成四個區:0~63為第0區,64~127為第1區,128~191為第2區,192~255為第3區。這意味著紅綠藍分別有4個區,總共可以構成64種組合(4的3次方)。
任何一種顏色必然屬於這64種組合中的一種,這樣就可以統計每一種組合包含的畫素數量。
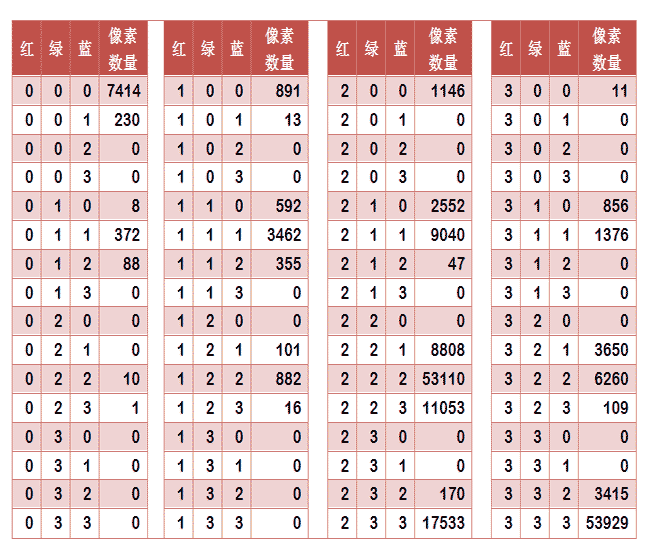
上圖是某張圖片的顏色分佈表,將表中最後一欄提取出來,組成一個64維向量(7414, 230, 0, 0, 8, ..., 109, 0, 0, 3415, 53929)。這個向量就是這張圖片的特徵值或者叫"指紋"。
於是,尋找相似圖片就變成了找出與其最相似的向量。這可以用皮爾遜相關係數或者餘弦相似度算出。
實現程式碼如下:


#include <opencv2/core.hpp> #include <opencv2/highgui.hpp> #include <opencv2/imgproc.hpp> #include <iostream> #include <algorithm> using namespace std; using namespace cv; void getRGBvector(const Mat&src, vector<unsigned int>& count)//得到64維向量 { int nRows = src.rows,nCols = src.cols * src.channels(); const uchar* p; for (int i = 0; i < nRows; ++i) { p = src.ptr<uchar>(i); for (int j = 0; j < nCols; j += 3) { int r = int(p[j])/64; int g = int(p[j + 1])/64; int b = int(p[j + 2])/64; count[r * 16 + g * 4 + b]++; } } } double getVectorLength(vector<unsigned int> &vec) { long long res = 0; for (int i = 0; i < vec.size(); i++) res += vec[i] * vec[i]; return sqrt(res); } double getcos(vector<unsigned int> &count1, vector<unsigned int> &count2) { double len1 = getVectorLength(count1); double len2 = getVectorLength(count2); assert(len1 != 0 && len2 != 0); long long sum = 0; for (int i = 0; i < count1.size(); i++) sum += count1[i] * count2[i]; return (double)sum / len1 / len2 >0 ? (double)sum / len1 / len2:0; } double getsimilarity(const Mat&src1, const Mat&src2) { vector<unsigned int> count1(64), count2(64); getRGBvector(src1, count1); getRGBvector(src2, count2); double res = getcos(count1, count2); return res; } int main() { Mat src1 = imread("晚霞1.jpg",1),src2 = imread("晚霞2.jpg", 1); imshow("src", src1),imshow("src", src2); double res = getsimilarity(src1,src2); cout << res << endl; waitKey(0); }

