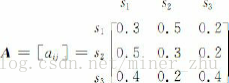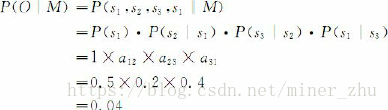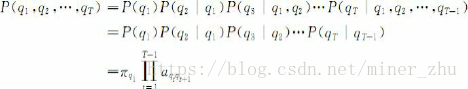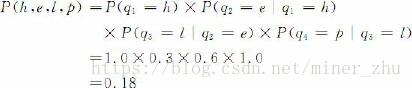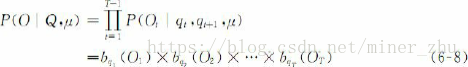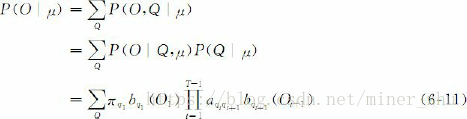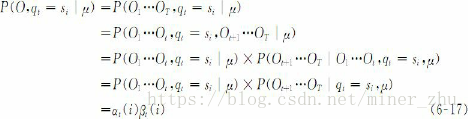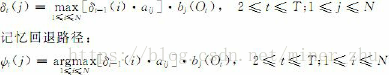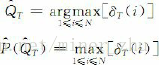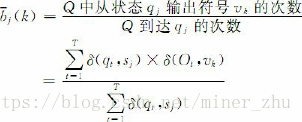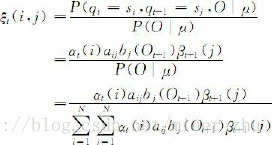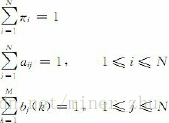NLP之隱馬爾可夫模型
馬爾可夫模型
在介紹隱馬爾可夫模型之前,先來介紹馬爾可夫模型。
我們知道,隨機過程又稱隨機函式,是隨時間而隨機變化的過程。 馬爾可夫模型(Markov model)描述了一類重要的隨機過程。我們常常需要考察一個隨機變數序列,這些隨機變數並不是相互獨立的,每個隨機變數的值依賴於這個序列前面的狀態。如果一個系統有N個有限狀態S={s1,s2,…,sN},那麼隨著時間的推移,該系統將從某一狀態轉移到另一狀態。Q=(q1,q2,…,qT)為一個隨機變數序列,隨機變數的取值為狀態集S中的某個狀態,假定在時間t的狀態記為qt。對該系統的描述通常需要給出當前時刻t的狀態和其前面所有狀態的關係:系統在時間t處於狀態sj的概率取決於其在時間1,2,…,t-1的狀態,該概率為
P(qt=sj|qt-1=si,qt-2=sk,…)
如果在特定條件下,系統在時間t的狀態只與其在時間t-1的狀態相關,即
則該系統構成一個離散的一階馬爾可夫鏈(Markov chain)。
進一步,如果只考慮式(6-1)獨立於時間t的隨機過程:
該隨機過程為馬爾可夫模型。
顯然,有N個狀態的一階馬爾可夫過程有N^2次狀態轉移,其N^2個狀態轉移概率可以表示成一個狀態轉移矩陣。例如,一段文字中名詞、動詞、形容詞三類詞性出現的情況可由三個狀態的馬爾可夫模型描述:
狀態s1:名詞
狀態s2:動詞
狀態s3:形容詞
假設狀態之間的轉移矩陣如下:
如果在該段文字中某一句子的第一個詞為名詞,那麼根據這一模型M,在該句子中這三類詞的出現順序為O=“名動形名”的概率為:
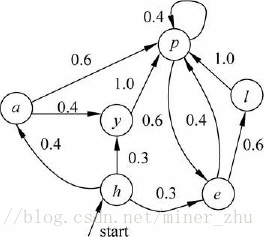
馬爾可夫模型又可視為隨機的有限狀態機。如下圖所示,圓圈表示狀態,狀態之間的轉移用帶箭頭的弧表示,弧上的數字為狀態轉移的概率,初始狀態用標記為start的輸入箭頭表示,假設任何狀態都可作為終止狀態。圖6-4中省略了轉移概率為0的弧,對於每個狀態來說,發出弧上的概率和為1。從圖可以看出,馬爾可夫模型可以看作是一個轉移弧上有概率的非確定的有限狀態自動機。
一個馬爾可夫鏈的狀態序列的概率可以通過計算形成該狀態序列的所有狀態之間轉移弧上的概率乘積而得出,即
根據上圖給出的狀態轉移概率,我們可以得到:
根據之前介紹的n元語法模型,當n=2時,實際上就是一個馬爾可夫模型。但是,當n≥3時,就不是一個馬爾可夫模型,因為它不符合馬爾可夫模型的基本約束。不過,對於n≥3的n元語法模型確定數量的歷史來說,可以通過將狀態空間描述成多重前面狀態的交叉乘積的方式,將其轉換成馬爾可夫模型。在這種情況下,可將其稱為m階馬爾可夫模型,這裡的m是用於預測下一個狀態的前面狀態的個數,那麼,n元語法模型就是n-1階馬爾可夫模型。
隱馬爾可夫模型(HMM)
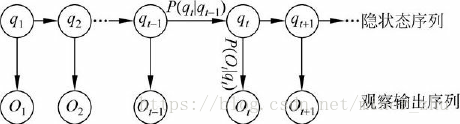
在馬爾可夫模型中,每個狀態代表了一個可觀察的事件,所以,馬爾可夫模型有時又稱作可視馬爾可夫模型(visible Markov model, VMM),這在某種程度上限制了模型的適應性。在隱馬爾可夫模型(HMM)中,我們不知道模型所經過的狀態序列,只知道狀態的概率函式,也就是說,觀察到的事件是狀態的隨機函式,因此,該模型是一個雙重的隨機過程。其中,模型的狀態轉換過程是不可觀察的,即隱蔽的,可觀察事件的隨機過程是隱蔽的狀態轉換過程的隨機函式。
可以用下面的圖6-5說明隱馬爾可夫模型的基本原理。
我們可以通過如下例子來說明HMM的含義。假定一暗室中有N個口袋,每個口袋中有M種不同顏色的球。一個實驗員根據某一概率分佈隨機地選取一個初始口袋,從中根據不同顏色的球的概率分佈,隨機地取出一個球,並向室外的人報告該球的顏色。然後,再根據口袋的概率分佈選擇另一個口袋,根據不同顏色的球的概率分佈從中隨機選擇另外一個球。重複進行這個過程。對於暗室外邊的人來說,可觀察的過程只是不同顏色的球的序列,而口袋的序列是不可觀察的。在這個過程中,每個口袋對應於HMM中的狀態,球的顏色對應於HMM中狀態的輸出符號,從一個口袋轉向另一個口袋對應於狀態轉換,從口袋中取出球的顏色對應於從一個狀態輸出的觀察符號。
通過上例可以看出,一個HMM由如下幾個部分組成:
(1) 模型中狀態的數目N(上例中口袋的數目);
(2) 從每個狀態可能輸出的不同符號的數目M(上例中球的不同顏色的數目);
(3) 狀態轉移概率矩陣A={aij}(aij為實驗員從一個口袋(狀態si)轉向另一個口袋(sj)取球的概率)
(4) 從狀態sj觀察到符號vk的概率分佈矩陣B={bj(k)}(bj(k)為實驗員從第j個口袋中取出第k種顏色的球的概率)
(5) 初始狀態概率分佈π={πi}
一般地,一個HMM記為一個五元組μ=(S,K,A,B,π),其中,S為狀態的集合,K為輸出符號的集合,π,A和B分別是初始狀態的概率分佈、狀態轉移概率和符號發射概率。為了簡單,有時也將其記為三元組μ=(A,B,π)。
當考慮潛在事件隨機地生成表面事件時,HMM是非常有用的。假設給定模型μ=(A,B,π),那麼,觀察序列O=O1O2…OT可以由下面的步驟直接產生:
(1) 根據初始狀態的概率分佈πi選擇一個初始狀態q1=si;
(2) 設t=1;
(3) 根據狀態si的輸出概率分佈bi(k)輸出Ot=vk;
(4) 根據狀態轉移概率分佈aij,將當前時刻t的狀態轉移到新的狀態qt+1=sj;
(5) t=t+1,如果t<T,重複執行步驟(3)和(4),否則,結束演算法。
HMM中有三個基本問題:
(1)估計問題:給定一個觀察序列O=O1O2…OT和模型μ=(A,B,π),如何快速地計算出給定模型μ情況下,觀察序列O的概率,即P(O|μ)?
(2)序列問題:給定一個觀察序列O=O1O2…OT和模型μ=(A,B,π),如何快速有效地選擇在一定意義下“最優”的狀態序列Q=q1q2…qT,使得該狀態序列“最好地解釋”觀察序列?
(3)訓練問題或引數估計問題:給定一個觀察序列O=O1O2…OT,如何根據最大似然估計來求模型的引數值?即如何調節模型μ=(A,B,π)的引數,使得P(O|μ)最大?
下面描述的前後向演算法及引數估計將給出這三個問題的解決方案。
1.1 解決第一個問題:前向演算法和後向演算法
給定一個觀察序列O=O1O2…OT和模型μ=(A,B,π),要快速地計算出給定模型μ情況下觀察序列O的概率,即P(O|μ)。這就是解碼(decoding)問題。
對於任意的狀態序列Q=q1q2…qT,有
並且
由於
因此
上述推導方式很直接,但面臨一個很大的困難是,必須窮盡所有可能的狀態序列。如果模型μ=(A,B,π)中有N個不同的狀態,時間長度為T,那麼,有N^T個可能的狀態序列。這樣,計算量會出現“指數爆炸”。當T很大時,幾乎不可能有效地執行這個演算法。為此,人們提出了前向演算法或前向計算過程(forward procedure),利用動態規劃的方法來解決這一問題,使“指數爆炸”問題可以在時間複雜度為O(N^2*T)的範圍內解決。
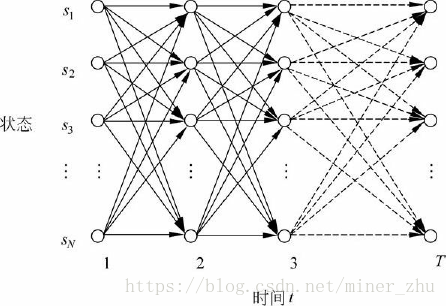
HMM中的動態規劃問題一般用格架(trellis或lattice)的組織形式描述。對於一個在某一時間結束在一定狀態的HMM,每一個格能夠記錄該HMM所有輸出符號的概率,較長子路徑的概率可以由較短子路徑的概率計算出來,如圖6-6所示
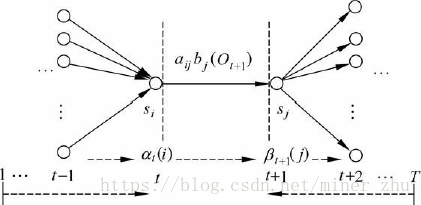
為了實現前向演算法,需要定義一個前向變數αt(i)。
定義6-1 前向變數αt(i)是在時間t,HMM輸出了序列O1O2…Ot,並且位於狀態si的概率
前向演算法的主要思想是,如果可以快速地計算前向變數αt(i),那麼,就可以根據αt(i)計算出P(O|μ),因為P(O|μ)是在所有狀態qT下觀察到序列O=O1O2…OT的概率:
在前向演算法中,採用動態規劃的方法計算前向變數αt(i),其實現思想基於如下觀察:在時間t+1的前向變數可以根據在時間t時的前向變數αt(1),αt(2),…,αt(N)的值來歸納計算:
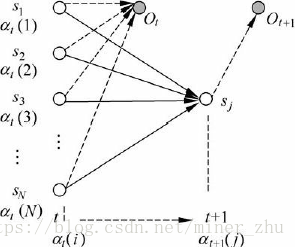
在格架結構中,αt+1(j)存放在(sj,t+1)處的結點上,表示在已知觀察序列O1O2…OtOt+1的情況下,從時間t到達下一個時間t+1時狀態為sj的概率。圖6-7描述了式(6-14)的歸納關係。
從初始時間開始到t+1,HMM到達狀態sj,並輸出觀察序列O1O2…Ot+1的過程可以分解為以下兩個步驟:
(1) 從初始時間開始到時間t,HMM到達狀態si,並輸出觀察序列O1O2…Ot;
(2) 從狀態si轉移到狀態sj,並在狀態sj輸出Ot+1。
這裡si可以是HMM的任意狀態。根據前向變數αt(i)的定義,從某一個狀態si出發完成第一步的概率就是αt(i),而實現第二步的概率為aij×bj(Ot+1)。因此,從初始時間到t+1整個過程的概率為:αt(i) ×aij×bj(Ot+1)。由於HMM可以從不同的si轉移到sj,一共有N個不同的狀態,因此,得到了式(6-14)。
根據式(6-14)給出的歸納關係,可以按時間順序和狀態順序依次計算前向變數α1(x),α2(x),…,αT(x)(x為HMM的狀態變數)。由此,得到如下前向演算法。
演算法6-1 前向演算法(forward procedure)
步1 初始化:α1(i)=πibi(O1), 1≤i≤N
步2 歸納計算:
步3 求和終結:
在初始化步驟中,πi是初始狀態si的概率,bi(O1)是在si狀態輸出O1的概率,那麼,πibi(O1)就是在時刻t=1時,HMM在si狀態輸出序列O1的概率,即前向變數α1(i)。一共有N個狀態,因此,需要初始化N個前向變數α1(1),α1(2),…,α1(N)。
現在我們來分析前向演算法的時間複雜性。由於每計算一個αt(i)必須考慮t-1時的所有N個狀態轉移到狀態si的可能性,其時間複雜性為O(N),那麼,對應每個時間t,要計算N個前向變數,αt(1), αt(2),…,αt(N),因此,時間複雜性為O(N)×N=O(N2)。因而,在1,2,…,T整個過程中,前向演算法的總時間複雜性為O(N2T)。
對於求解HMM中的第一個問題,即在給定一個觀察序列O=O1O2…OT和模型μ=(A,B,π)情況下,快速計算P(O|μ)的問題還可以採用另外一種實現方法,即後向演算法。
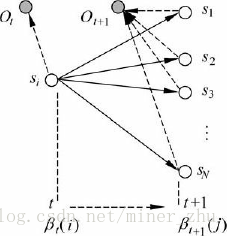
定義6-2 後向變數βt(i)是在給定了模型μ=(A,B,π),並且在時間t狀態為si的條件下,HMM輸出觀察序列Ot+2…OT的概率:
與計算前向變數一樣,可以用動態規劃的演算法計算後向變數。類似地,在時間t狀態為si的條件下,HMM輸出觀察序列Ot+1Ot+2…OT的過程可以分解為以下兩個步驟:
(1) 從時間t到時間t+1,HMM由狀態si到狀態sj,並從sj輸出Ot+1;
(2) 在時間t+1的狀態為sj的條件下,HMM輸出觀察序列Ot+2…OT。
第一步中輸出Ot+1的概率為:aij×bj(Ot+1);第二步中根據後向變數的定義,HMM輸出觀察序列為Ot+2…OT的概率就是後向變數βt+1(j)。於是,得到如下歸納關係:
式(6-16)的歸納關係可以由圖6-8來描述。
根據後向變數的歸納關係,按T,T-1,…,2,1順序依次計算βT(x),βT-1(x),…,β1(x)(x為HMM的狀態),就可以得到整個觀察序列O=O1O2…OT的概率。下面的後向演算法用於實現這個歸納計算的過程。
演算法6-2 後向演算法(backward procedure)
步1 初始化:βT(i)=1,1≤i≤N
步2 歸納計算:
步3 求和終結:
類似於前向演算法的分析,可知後向演算法的時間複雜度也是O(N2T)。更一般地,實際上我們可以採用前向演算法和後向演算法相結合的方法來計算觀察序列的概率:
因此
1.2 解決第二個問題:維特比演算法
維特比(Viterbi)演算法用於求解HMM中的第二個問題,即給定一個觀察序列O=O1O2…OT和模型μ=(A,B,π),如何快速有效地選擇在一定意義下“最優”的狀態序列Q=q1q2…qT,使得該狀態序列“最好地解釋”觀察序列。這個問題的答案並不是唯一的,因為它取決於對“最優狀態序列”的理解。
一種理解是,使該狀態序列中每一個狀態都單獨地具有最大概率,即要使得:最大
根據貝葉斯公式,有
參考式(6-17)和式(6-18),並且P(qt=si,O|μ)=P(O,qt=si|μ),因此
有了γt(i),那麼,在時間t的最優狀態為
根據這種對“最優狀態序列”的理解,如果只考慮使每個狀態的出現都單獨達到最大概率,而忽略了狀態序列中兩個狀態之間的關係,很可能導致兩個狀態之間的轉移概率為0,即=0。那麼,在這種情況下,所謂的“最優狀態序列”根本就不是合法的序列。
因此,我們常常採用另一種對“最優狀態序列”的理解:在給定模型μ和觀察序列O的條件下,使條件概率P(Q|O,μ)最大的狀態序列。即
這種理解避免了前一種理解引起的“斷序”的問題。根據這種理解,優化的不是狀態序列中的單個狀態,而是整個狀態序列,不合法的狀態序列的概率為0,因此,不可能被選為最優狀態序列。
維特比演算法運用動態規劃的搜尋演算法求解這種最優狀態序列。為了實現這種搜尋,首先定義一個維特比變數δt(i)。
定義6-3 維特比變數δt(i)是在時間t時,HMM沿著某一條路徑到達狀態si,並輸出觀察序列O1O2…Ot的最大概率:
與前向變數類似,δt(i)有如下遞迴關係:
這種遞迴關係使我們能夠運用動態規劃搜尋技術。為了記錄在時間t時,HMM通過哪一條概率最大的路徑到達狀態si,維特比演算法設定了另外一個變數ψt(i)用於路徑記憶,讓ψt(i)記錄該路徑上狀態si的前一個(在時間t-1的)狀態。根據這種思路,給出如下維特比演算法。
演算法6-3 維特比演算法(Viterbi algorithm)
步1 初始化:
步2 歸納計算:
步3 求和終結:
步4 路徑(狀態序列)回溯:
維特比演算法的時間複雜性與前向演算法、後向演算法的時間複雜性一樣,也是O(N2T)。
在實際應用中,往往不只是搜尋一個最優狀態序列,而是搜尋n個最佳(n-best)路徑,因此,在格架的每個結點上常常需要記錄m個最佳(m-best, m<n)狀態。
1.3 解決第三個問題:引數估計
引數估計問題是HMM面臨的第三個問題,即給定一個觀察序列O=O1O2…OT,如何調節模型μ=(A,B,π)的引數,使得P(O|μ)最大化:
模型的引數是指構成μ的πi,aij,bj(k)。最大似然估計方法可以作為HMM引數估計的一種選擇。如果產生觀察序列O的狀態序列Q=q1q2…qT已知,根據最大似然估計,HMM的引數可以通過如下公式計算:
其中,δ(x, y)為克羅奈克(Kronecker)函式,當x=y時,δ(x, y)=1;否則,δ(x, y)=0。vk是HMM輸出符號集中的第k個符號。
但實際上,由於HMM中的狀態序列Q是觀察不到的(隱變數),因此,這種最大似然估計的方法不可行。所幸的是,期望最大化(expectation maximization, EM)演算法可以用於含有隱變數的統計模型的引數最大似然估計。其基本思想是,初始時隨機地給模型的引數賦值,該賦值遵循模型對引數的限制,例如,從某一狀態出發的所有轉移概率的和為1。給模型引數賦初值以後,得到模型μ0,然後,根據μ0可以得到模型中隱變數的期望值。例如,從μ0得到從某一狀態轉移到另一狀態的期望次數,用期望次數來替代式(6-23)中的實際次數,這樣可以得到模型引數的新估計值,由此得到新的模型μ1。從μ1又可以得到模型中隱變數的期望值,然後,重新估計模型的引數,執行這個迭代過程,直到引數收斂於最大似然估計值。
這種迭代爬山演算法可以區域性地使P(O|μ)最大化。Baum-Welch演算法或稱前向後向演算法(forward-backward algorithm)用於具體實現這種EM方法。下面我們介紹這種演算法。
給定HMM的引數μ和觀察序列O=O1O2…OT,在時間t位於狀態si,時間t+1位於狀態sj的概率ξt(i,j)=P(qt=si,qt+1=sj|O,μ)(1≤t≤T,1≤i, j≤N)可以由下面的公式計算獲得:
圖6-9給出了式(6-24)所表達的前向變數αt(i)、後向變數βt+1(j)與概率ξt(i, j)之間的關係。
給定HMM μ和觀察序列O=O1O2…OT,在時間t位於狀態si的概率γt(i)為
由此,μ的引數可以由下面的公式重新估計:
根據上述思路,給出如下前向後向演算法。
演算法6-4 前向後向演算法(forward-backward algorithm)
步1 初始化:隨機地給引數πi,aij,bj(k)賦值,使其滿足如下約束:
由此得到模型μ0。令i=0,執行下面的EM估計。
步2 EM計算:
E-步驟:由模型μi根據式(6-24)和式(6-25)計算期望值ξt(i, j)和γt(i);
M-步驟:用E-步驟得到的期望值,根據式(6-26)、(6-27)和(6-28)重新估計引數πi,aij,bj(k)的值,得到模型μi+1。
步3 迴圈計算:
令i=i+1。重複執行EM計算,直到πi,aij,bj(k)收斂。
HMM在自然語言處理研究中有著非常廣泛的應用。需要提醒的是,除了上述討論的理論問題以外,在實際應用中還有若干實現技術上的問題需要注意。例如,多個概率連乘引起的浮點數下溢問題。在Viterbi演算法中只涉及乘法運算和求最大值問題,因此,可以對概率相乘的算式取對數運算,使乘法運算變成加法運算,這樣一方面避免了浮點數下溢的問題,另一方面,提高了運算速度。在前向後向演算法中,也經常採用如下對數運算的方法判斷引數πi,aij,bj(k)是否收斂:|log P(O|μi+1)-log P(O|μi)|<ε其中,ε為一個足夠小的實數值。但是,在前向後向演算法中執行EM計算時有加法運算,這就使得EM計算中無法採用對數運算,在這種情況下,可以設定一個輔助的比例係數,將概率值乘以這個比例係數以放大概率值,避免浮點數下溢。在每次迭代結束重新估計引數值時,再將比例係數取消。