資料結構與演算法之美專欄學習筆記-二叉樹基礎(上)
阿新 • • 發佈:2018-11-13
樹
節點的定義
樹中的元素稱之為節點
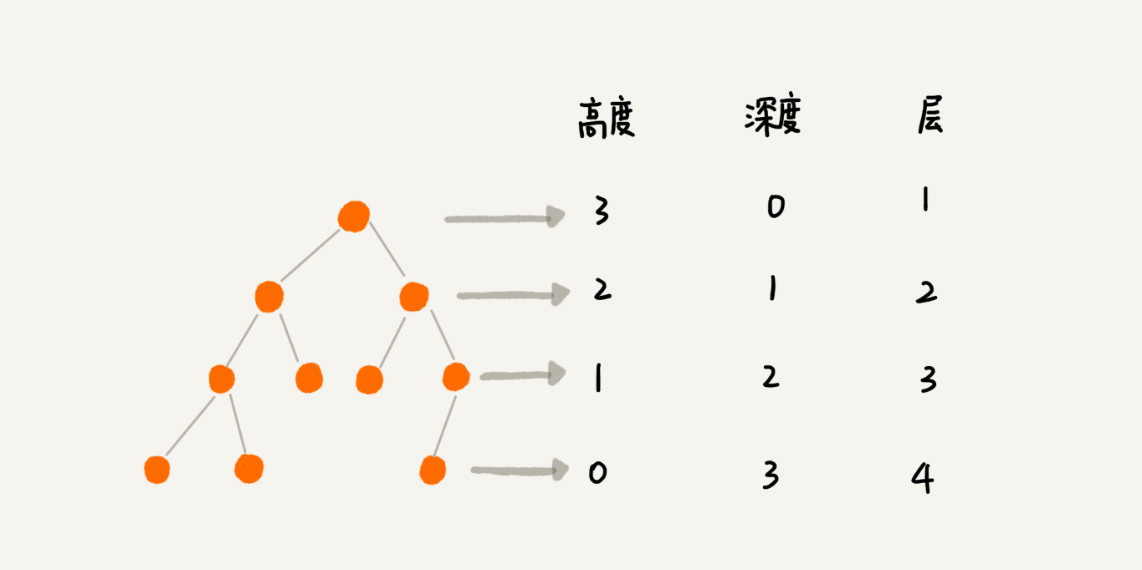
高度的定義
節點的高度:節點到葉子節點的最長路徑
樹的高度:跟節點的高度
深度的定義
根節點到這個節點所經歷的邊的個數
層的定義
節點的深度+1
二叉樹
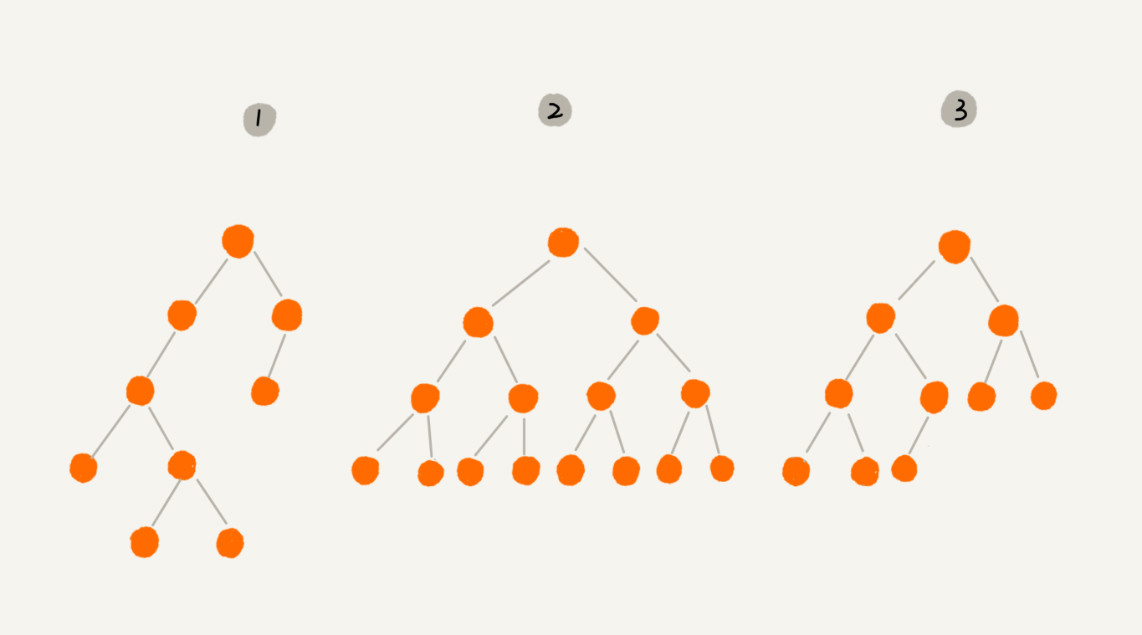
滿二叉樹
除了葉子結點外每個節點都有左右兩個子節點
完全二叉樹
葉子結點都在最低下兩層,最後一層的葉子節點都靠左排列,並且除了最後一層,其他層的節點個數都要達到最大
表示、儲存一顆二叉樹
鏈式儲存法
每個結點有三個欄位,其中一個儲存資料,另兩個是指向左右子節點的指標。

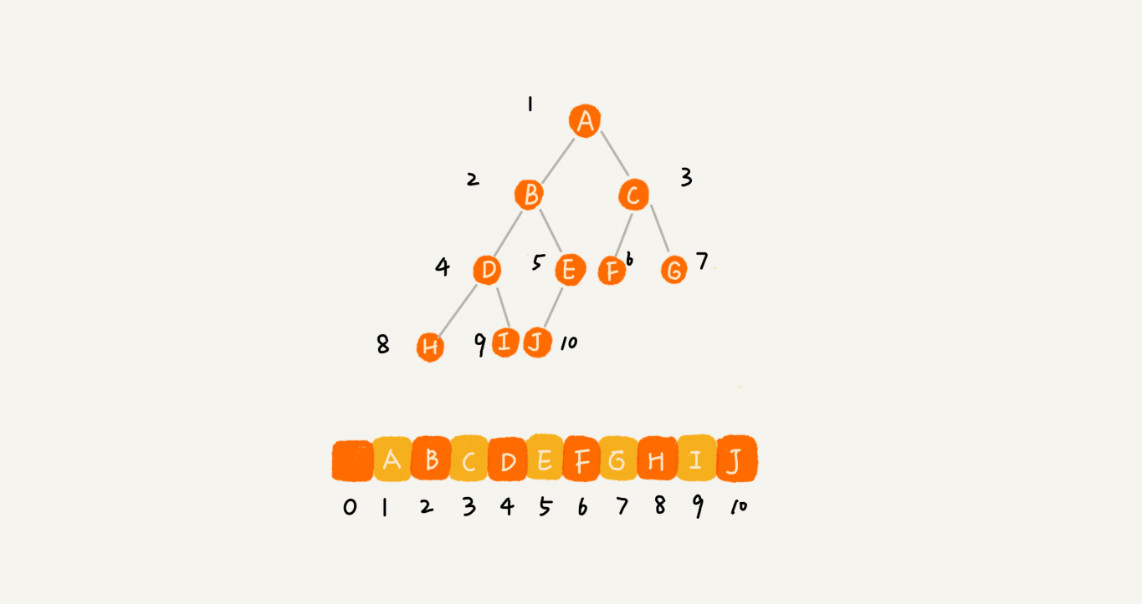
順序儲存法(基於陣列)
根節點儲存在下標i=1的位置,左子節點儲存在下標2*i=2的位置,右子節點儲存在2*i+1=3的位置,以此類推。
如果節點 X 儲存在陣列中下標為 i 的位置,下標為 2 * i 的位置儲存的就是左子節點,下標為 2 * i + 1 的位置儲存的就是右子節點。
我們只要知道根節點儲存的位置,這樣就可以通過下標計算,把整棵樹都串起來。
為了方便計運算元節點,根節點會儲存在下標為 1 的位置
程式碼實現
二叉樹的遍歷
前序遍歷
對於樹中的任意節點來說,先列印這個節點,然
後再列印它的左子樹,最後列印它的右子樹。
中序遍歷
對於樹中的任意節點來說,先列印它的左子樹,
然後再列印它本身,最後列印它的右子樹。
後序遍歷
對於樹中的任意節點來說,先列印它的左子樹,
然後再列印它的右子樹,最後列印這個節點本身。

實際上,二叉樹的前、中、後序遍歷就是一個遞迴的過程。
比如,前序遍歷,其實就是先列印根節點,然後再遞迴地列印左子樹,最後遞迴地列印右子樹。
遍歷程式碼實現
